| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
二、填空题: 13、 14、 15、 16、 三、解答题: 17、 18、
20、 21、
22、 2008届高三数学(理科)模拟试题(三)参考答案 一、1 B 2 D 二、13、3 14、-160 15、 三、17、解: (1)
(2)
18、(I)解:设这箱产品被用户拒绝接收事件为A,被接收为
即这箱产品被用户拒绝接收的概率为 (II)
|
| 1
| 2
| 3
| P
|
|
|
|
…………11分
∴ E ![]()
![]()
19、解法一:
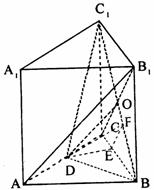 (Ⅰ)连结B
(Ⅰ)连结B![]()
![]()
∵在△A ![]()
∴A ![]()
∵A ![]()
![]()
![]()
![]()
![]()
∴A ![]()
![]()
(Ⅱ)设正三棱柱底面边长为2,则DC = 1。
∵∠ ![]()
![]()
![]()
作DE⊥BC于E。
∵平面BC ![]()
∴DE⊥平面BC ![]()
![]()
作EF⊥B ![]()
![]()
∴∠DFE是二面角D-B ![]()
在Rt△DEC中,DE= ![]()
在Rt△BFE中,EF = BE·sin ![]()
∴在Rt△DEF中,tan∠DFE = ![]()
 ∴二面角D-B
∴二面角D-B ![]()
![]()
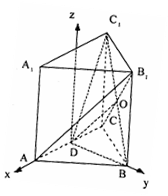
解法二:以AC的中D为原点建立坐标系,如图,
设| AD | = 1∵∠ ![]()
![]()
![]()
则A(1,0,0),B(0, ![]()
![]()
![]()
![]()
![]()
(Ⅰ)连结 ![]()
![]()
![]()
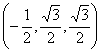
![]()
![]()
∵A ![]()
![]()
![]()
∴A ![]()
![]()
(Ⅱ) ![]()
![]()
![]()
设平面B ![]()
![]()
即 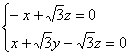
![]()
则n = ( ![]()
设平面BC ![]()
![]()
|
|
|
|
|
|
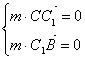
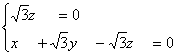
![]() 令y = -1,解得m = (
令y = -1,解得m = ( ![]()
二面角D —B ![]()
∴二面角D—B ![]()
![]()
20、解: 对函数 ![]()
![]()
(Ⅰ)当 ![]()
![]()
令 ![]()
![]()
![]()
![]()
![]()
所以, ![]()
![]()
![]()
![]()
(Ⅱ) 令 ![]()
![]()
![]()
![]()
由 ![]()
x
![]()
![]()
![]()
1
![]()
![]()
0
-
0
![]()
![]()
极大值
![]()
极小值
![]()
……………8分
对于 ![]()
![]()
![]()
∴ ![]()
对于 ![]()
![]()
![]()
所以,当 ![]()
![]()
由题意,不等式 ![]()
![]()
所以得 ![]()
![]()
21、解: (I)依题意知,点 ![]()
![]()
![]()
离心率为 ![]()
设椭圆的长轴长为
又 ![]()
![]()
![]()
![]()
![]()
![]()
解之得: ![]()
![]()
![]()
∴坐标原点 ![]()
![]()
∴动点M的轨迹方程为: ![]()
![]() ………… 4分
………… 4分
(II)设 ![]()
![]()
![]()
![]()
![]()
![]() ………… 5分
………… 5分
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
解得: ![]()
![]()
![]() ∴ 直线EF在X轴上的截距为
∴ 直线EF在X轴上的截距为 ![]()
(Ⅲ)设 ![]()
![]()
![]()
![]()
直线 ![]()
![]()
![]() ………… 10分
………… 10分
当 ![]()
![]()
当 ![]()
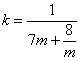
![]()
![]()
![]()
综上所述 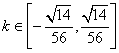
![]()
22、(I)解:方程 ![]()
![]()
![]()
当 ![]()
![]()
![]()
当 ![]()
![]()
![]()
![]()
当 ![]()
![]()
![]()
![]()
当 ![]()
![]()
![]()
![]()
![]()
(II)解: ![]()
![]()
![]()
![]()
(III)证实: ![]()
所以 ![]()
![]()
![]()
当 ![]()
![]()
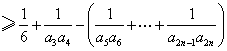
![]()
![]()
![]()
同时, ![]()
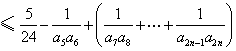
![]()
![]()
![]()
综上,当 ![]()
![]()
![]()
| |