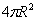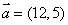lang=ZH-CN link="#261CDC" vlink=purple >
08届高考文科数学模拟试卷(五)
一、选择题:(本大题共12小题,每小题5分,共60分,)
1.已知全集U=  ;集合M=
;集合M=  ;N=
;N= 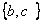 ,则M
,则M  =
=
A.  B.
B. 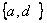 C.
C.  D.
D. 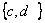
2. 在求简单对数不等式中,形成下列变式题:①对于 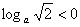 ,则
,则 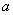 的范围是
的范围是 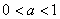 ;
;
②对于  ,则
,则 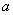 的范围是
的范围是  ;③对于
;③对于 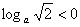 ,则
,则 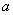 的范围是
的范围是  ;
;
则上述求解正确的是
A. ①② B. ②③ C. ①③ D. ①②③
3.已知数据  的平均数
的平均数  ,方差
,方差 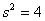 ,则数据
,则数据  的平均数和标准差分别是
的平均数和标准差分别是
A. 22,36 B.22,6 C.20,6 D.15,36
4.设函数  ,则
,则 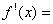
A.  B.
B.  C.
C. 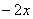 D.
D. 
5.向量 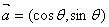 ,向量
,向量 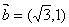 ,则
,则 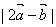 最大值为
最大值为
A. 3 B. 4 C. 5 D.6
6.若直线  与圆
与圆 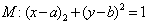 相交于A、B两点且|AB|=
相交于A、B两点且|AB|= 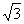 ,则
,则 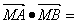
A. 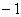 B.1 C.
B.1 C. 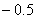 D.不能确定
D.不能确定
7. 某卫星发射场实验区用四根垂直于水平地面的立柱支撑一个平行四边形的太阳能电池板,现在测得其中的三根立柱AA1 ,BB1,CC1,的长度分别为10m,15m,30m.则柱DD1=
A. 20m B. 25m C.30m D.35m
8. 在  的展开式中,
的展开式中, 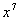 的系数是
的系数是
A. 6 B.  C. 5 D.
C. 5 D. 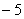
9.已知函数  ,则它们的图象经过平移后能够重合的是
,则它们的图象经过平移后能够重合的是
A.  ,
,  ,
, 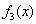 重合但不能与
重合但不能与 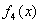 重合 B.
重合 B.  ,
, 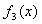 ,
, 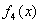 重合但不能与
重合但不能与  重合
重合
C.  ,
, 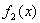 重合;
重合;  ,
, 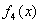 重合 D.
重合 D.  ,
, 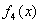 重合;
重合; 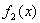
 重合
重合
10. 已知集合M= 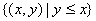 ,P=
,P=  ,S=
,S= 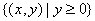 ,若
,若  ,
,
点  的最大值是
的最大值是
A. 0 B. 2 C. 3 D. 4
11.设  是
是 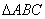 的三个内角,且
的三个内角,且  ,
,  ,则这样的数组
,则这样的数组 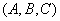 的个数为
的个数为
A. 8 B. 36 C. 3 D.10
12. 设  是
是 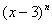 的展开式中含
的展开式中含  项的系数,则
项的系数,则 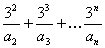 的值为
的值为
A. 16 B. 17 C.18 D.19
二、填空题(本大题共有4个小题,每小题4分,共16分.)
13.已知抛物线 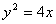 的准线是圆
的准线是圆 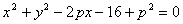 的一条切线,则圆的另一条垂直于
的一条切线,则圆的另一条垂直于 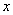 轴的切线方程是 。
轴的切线方程是 。
14.已知函数 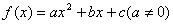 ,不等式
,不等式 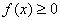 的解集为
的解集为 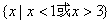 ,
,
则不等式  的解集是 。
的解集是 。
15.平面向量也称二维向量,其坐标表示及其运算可以推广到n(n>2)维向量,n维向量的坐标为 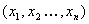 ;设
;设  ,
, 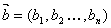 ,规定
,规定 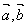 的夹角
的夹角 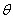 的余弦
的余弦 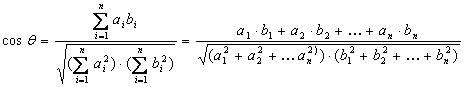 ,若
,若  ,
, 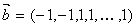 (前两个是
(前两个是 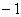 ,其余都是1),则
,其余都是1),则 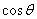 = 。
= 。
16.数轴Ox,Oy的夹角为  ,设P为斜坐标系xOy平面上的任意一点,
,设P为斜坐标系xOy平面上的任意一点,  是Ox,Oy轴正方向上的单位向量,若
是Ox,Oy轴正方向上的单位向量,若  ,则称P的斜坐标是
,则称P的斜坐标是 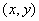 ,已知斜坐标
,已知斜坐标 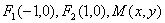 的点,满足
的点,满足  ,则动点
,则动点  的轨迹方程是 。
的轨迹方程是 。
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证实过程或演算步骤.)
17. 已知锐角 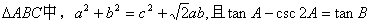 。
。
(1)求证 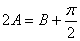 ;(2)求角
;(2)求角  的大小。
的大小。
18. 已知数列{ 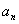 }满足
}满足 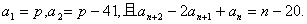 (其中
(其中 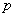 是给定的实常数)。又
是给定的实常数)。又 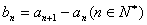 。
。
(1)求数列{ 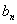 }的通项公式; (2)求
}的通项公式; (2)求 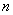 的值,使得{
的值,使得{ 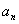 }的最小。
}的最小。
19.一个口袋内有2个不同的红球和4个不同的白球。
(1)从中任取3个球,求白球的个数不少于红球的概率;
(2)若取一个红球得2分,取一个白球得1分,从中任取4个球,求总分不少于5分的概率。
20.如图,已知直三棱柱 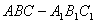 的侧棱长为2,
的侧棱长为2, 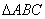 是
是
等腰三角形,且 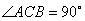 ,
,  ,
,  是
是 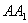 的中点。
的中点。
(1)求异面直线 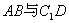 所成的角;
所成的角;
(2)若E为AB上一点,试确定E的位置,使得 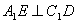 ;
;
(3)在(2)的条件下,求点D到平面 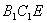 的距离
的距离
21. .如图,过抛物线 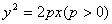 的焦点F的直线
的焦点F的直线 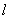 交抛物线
交抛物线
于A,B两点,交其准线于点C,若|BC|=2|BF|,且|AF|=4。
(1)求直线 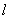 的方程和抛物线的方程;
的方程和抛物线的方程;
(2)过焦点F任作直线MN与抛物线 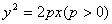 相交于M,
相交于M,
N两点,E是其准线上的任意一点,求证:直线EM,EF,EN的斜
率  ,
, 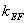 ,
, 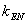 成等差数列。
成等差数列。
22.设函数 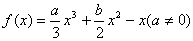 ,在点
,在点 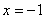 处取极值,且在
处取极值,且在 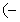 1,1)内是单调函数。
1,1)内是单调函数。
(1)求证:| 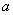 |≤1;
|≤1;
(2)若 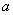 >0, 且在
>0, 且在 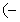 1,1)内有
1,1)内有 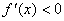 ,试求
,试求 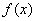 的极大值的取值范围.
的极大值的取值范围.
参考答案
1.答案A,  ,∴
,∴ 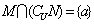 2.答案C,画出函数图象比较即可得结论①③正确, ②错误.
2.答案C,画出函数图象比较即可得结论①③正确, ②错误.
3.答案B,由 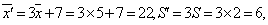 4.答案D,
4.答案D, 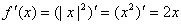
5.答案B,设 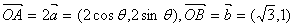 ,则
,则 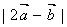 的几何意义是点
的几何意义是点 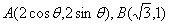 两点之间的距离|AB|,且点A,B同在以O点为圆心,以2为半径的圆上, ∴
两点之间的距离|AB|,且点A,B同在以O点为圆心,以2为半径的圆上, ∴ 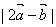 的最大值是4. 6. 答案C,过圆心M作
的最大值是4. 6. 答案C,过圆心M作  于N,,则
于N,,则 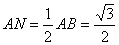 ,∴
,∴ 
7.答案B,设AC,BD相交于点O,则O为平行四边形ABCD的中心,∴  10 30-15=25. 8.答案B,
10 30-15=25. 8.答案B,  , ∴
, ∴ 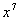 的系数是
的系数是 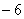 . 9.答案D,
. 9.答案D,  ,
, 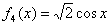 ,
, 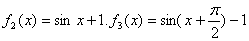 , 10.答案D,设
, 10.答案D,设 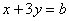 ,则当
,则当 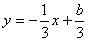 过(1,1)时
过(1,1)时  取最大值是4。11.答案A,
取最大值是4。11.答案A,  ,
,  ,
, 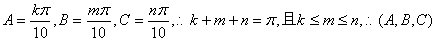 共有8组解。
共有8组解。
12.答案B, 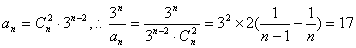 。
。
13.答案: 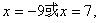 抛物线
抛物线 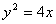 的准线方程是
的准线方程是 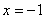 ,而圆方程是
,而圆方程是 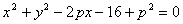 ,又
,又  在圆上,
在圆上,  即
即 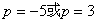 。
。
14.答案:  ,提示由已知得
,提示由已知得 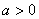 ,所以不等式
,所以不等式 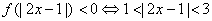
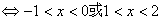 。
。
15.答案: 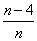 ,提示:
,提示: 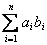 中正负抵消4项,而
中正负抵消4项,而 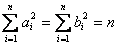 。
。
16.答案: 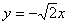 ,提示:
,提示: 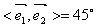 ,
,  ,
,  ,
,  ,
,
而 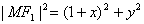
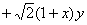 ,
, 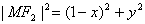
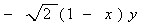 。
。
17.解:(1) 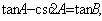
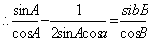 ,
, 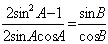
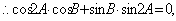

 ,
, 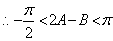 ,即
,即 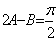 ,所以有
,所以有 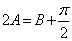 。
。
(2)由 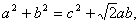 得
得  ,
, 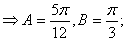 所以
所以  。
。
18.解:(1)由已知 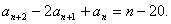 及
及 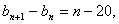
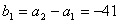 ,
,
由累加法可得: 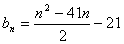 。
。
(2)由 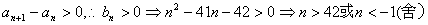 ,故
,故  ,有
,有  ,
, 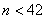 ,有
,有  ,
, 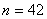 ,有
,有 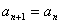 ,则
,则  时,
时, 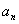 最小。
最小。
19.解:从袋中取3个球的事件总数为  种,设“取3个球中,白球的个数不少于红球的事件”为A,从事件A取出3个球中:2个白球,1个红球或3个白球,则事件A的基本事件数为
种,设“取3个球中,白球的个数不少于红球的事件”为A,从事件A取出3个球中:2个白球,1个红球或3个白球,则事件A的基本事件数为 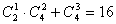 种,所以
种,所以 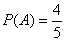 ,即所求概率为
,即所求概率为  。
。
(2)从袋中取4个球的事件总数为 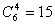 种,设“取一个红球得2分,取一个白球得1分,从中任取4个球,求总分不少于5分”的事件为B,5分情况有:① 2,2,1,1;②2,1,1,1.即4个球中至少有一个红球,故事件B的对立事件
种,设“取一个红球得2分,取一个白球得1分,从中任取4个球,求总分不少于5分”的事件为B,5分情况有:① 2,2,1,1;②2,1,1,1.即4个球中至少有一个红球,故事件B的对立事件  为“取出个球中全是白球”,则事件
为“取出个球中全是白球”,则事件  的基本事件数为
的基本事件数为 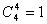 ,故
,故 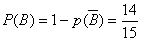 ,即所求概率为
,即所求概率为 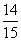 .
.
20.解:(1)取 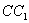 的中点F,连结AF,BF,则
的中点F,连结AF,BF,则 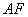 ∥
∥ 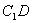 ,
,  所以
所以 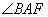 是异面直线AB与
是异面直线AB与 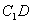 所成的角或
所成的角或
补角,因为 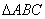 是等腰直角三角形,AC=2,所以AB=
是等腰直角三角形,AC=2,所以AB= 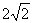 .又因为
.又因为 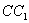 =2,所以AF=BF=
=2,所以AF=BF=  ,
,
所以 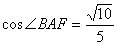 ,故异面直线AB与
,故异面直线AB与 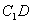 所成的角是
所成的角是 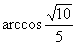 .
.
(2)过  作
作 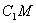
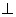
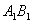 于
于  ,则
,则  为
为 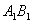 的中点,
的中点, 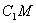
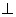 平面
平面 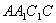 。连结
。连结 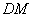 ,则
,则 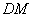 为
为 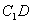 在平面
在平面 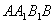 的射影。要使得
的射影。要使得  ,因为
,因为  ,可得
,可得 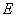 为AB的中点。
为AB的中点。
(3)取 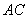 的中点N,连结
的中点N,连结 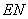 ,
,  ,则
,则 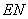 ∥
∥  ,因为
,因为 
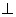 平面
平面 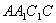 ,所以平面
,所以平面 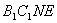
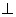 平面
平面 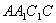 。过点
。过点  作
作 
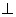
 于H,则
于H,则 
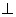 平面
平面 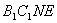 ,所以
,所以  的长度为点
的长度为点  到平面
到平面 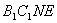 的距离。在正方形
的距离。在正方形 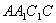 ,得
,得 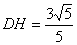 。即点
。即点  到平面
到平面 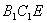 的距离为
的距离为 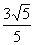 。
。
21.解:(1)分别过点 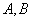 作准线的垂线
作准线的垂线 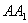 ,
, 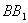 ,垂足分别为
,垂足分别为 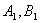 ,由抛物线的定义知
,由抛物线的定义知 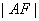 =
=  ,
, 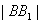 =
= 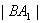 ,
, 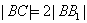 ,在
,在 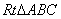 中,
中, 
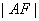
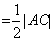 ,即
,即  为线段
为线段 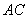 的中点,
的中点, 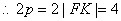 。所以抛物线的方程为
。所以抛物线的方程为 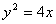 ,直线方程为
,直线方程为 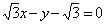 。
。
(2)因为直线EM,EF,EN的斜率分别为  ,
, 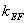 ,
, 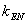 ,
, 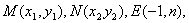 则
则 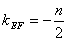 ,直线MN的方程设为
,直线MN的方程设为  ,代人
,代人 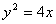 ,得
,得  ,
, 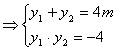 ,
, 
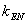

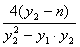
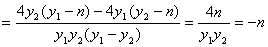

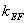 ,
,
即直线EM,EF,EN的斜率成等差数列。
22.(1)证实: 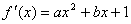 ,因为
,因为 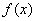 在
在 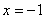 处取极值,所以
处取极值,所以 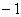 是方程
是方程 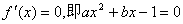 的根,所以
的根,所以  的解集为{
的解集为{ 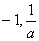 },且
},且 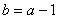 。所以
。所以 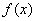 在点
在点 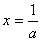 处取极值,所以
处取极值,所以  ,故
,故 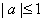 。
。
(2)由 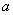 >0,
>0, 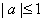
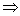
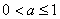 ,所以
,所以 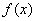 在
在  ,
, 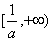 上是单调增函数。所以
上是单调增函数。所以 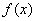 的极大值为
的极大值为 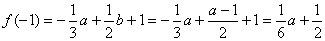 ,又因为
,又因为 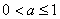 ,所以
,所以 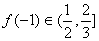 。
。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
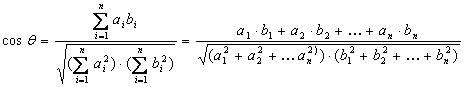
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
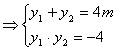
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()