|
|
 |
| 中文域名: 古今中外.com
英文域名:www.1-123.com 丰富实用的教育教学资料 |
| |
|
[组图]高三文科数学第五次考试试题
|
| 查询数高三上末的详细结果
|
|
高三文科数学第五次考试试题
数 学(文科)试卷
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
(1)设集合 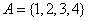 ,集合
,集合 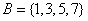 ,则
,则 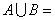
(A) 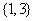 (B)
(B) 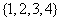 (C)
(C) 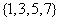 (D)
(D) 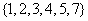
﹙2﹚函数  的定义域是
的定义域是
(A) 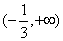 (B)
(B)  (C)
(C) 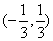 (D)
(D) 
(3) “  ”是“
”是“ 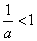 ”成立的
”成立的
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既非充分也非必要条件
(4)在等差数列  中,已知
中,已知 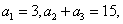 则
则  等于
等于
(A)45 (B)43 (C)42 (D)40
(5)下列函数中,在其定义域内是增函数的是
(A) 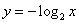 (
( 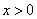 ) (B)
) (B)  (
(  )
)
(C) 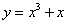 (
(  ) (D)
) (D)  (
(  ,
, 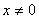 )
)
(6)在1,2,3,4,5这五个数字组成的无重复数字的三位数中,奇数共有
(A)9个 (B)18个 (C) 36个 (D)40个
(7)给出下列命题:
①假如函数  对任意的
对任意的  ,满足
,满足 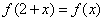 ,那么函数
,那么函数  是周期函数;
是周期函数;
②假如函数  对任意
对任意 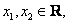 且
且 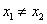 ,都有
,都有  ,那么函数
,那么函数  在
在 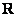 上是增函数;
上是增函数;
③假如函数  对任意的
对任意的  ,都有
,都有 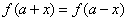 (
( 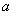 是常数),那么函数
是常数),那么函数  必为偶函数.
必为偶函数.
其中真命题有
(A)3个 (B)2个 (C)1个 (D)0个
(8)假如数列 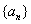 满足:首项
满足:首项 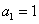 ,且
,且 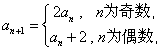 那么下列说法中正确的是
那么下列说法中正确的是
(A)该数列的奇数项 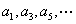 成等比数列,偶数项
成等比数列,偶数项  成等差数列
成等差数列
(B)该数列的奇数项 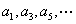 成等差数列,偶数项
成等差数列,偶数项  成等比数列
成等比数列
(C)该数列的奇数项 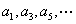 分别加4后构成一个公比为2的等比数列
分别加4后构成一个公比为2的等比数列
(D)该数列的偶数项  分别加4后构成一个公比为2的等比数列
分别加4后构成一个公比为2的等比数列
二、填空题:本大题共6小题,每小题5分,共30分.请把答案填在题中横线上.
(9)函数  的反函数
的反函数 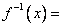 ,其定义域为 .
,其定义域为 .
(10)函数 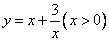 的最小值为 .
的最小值为 .
(11)  展开式中的常数项是 .(用数字作答)
展开式中的常数项是 .(用数字作答)
(12)数列{an}是公差不为0的等差数列,且a1, a3, a7为等比数列{bn}的连续三项,则等比数列{bn}的公比 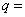 .
.
(13)若不等式  对于一切
对于一切  恒成立,则实数
恒成立,则实数 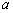 的取值范围为_ __ .
的取值范围为_ __ .
(14)近年来,在欧美等国家流行一种“数独”推理游戏,游戏规则如下: |
|
|
4 |
|
|
|
|
|
| |
|
9 |
|
3 |
5 |
|
|
|
7 | |
2 |
|
|
6 |
|
|
3 |
5 |
|
|
4 |
2 |
8 |
|
6 |
9 |
|
| |
|
1 |
|
|
A |
|
|
7 |
| |
|
|
6 |
9 |
|
3 |
5 |
4 |
| |
|
2 |
8 |
|
|
9 |
|
|
5 | |
1 |
|
|
|
2 |
8 |
|
6 |
| |
|
|
|
|
|
|
4 |
|
| |
① 在9×9的九宫格子中,分成9个3×3的小九宫格,用1到9这9个数字填满整个格子;
② 每一行与每一列都有1到9的数字,每个小九宫格里也有1到9的数字,并且一个数字在每行、每列及每个小九宫格里只能出现一次,既不能重复也不能少.
图中A处应填入的数字为_______;若每行每列填满数字后,所有数字之和为________.
三、解答题:本大题共6小题,共80分.解答应写出文字说明、演算步骤或证实过程.
(15)(本小题共13分)
已知全集 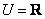 ,集合
,集合 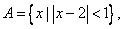 集合 集合 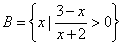 .
.
(I)求 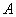 ,
, 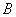 ;
;
(II) 求 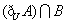 .
.
(16)(本小题共14分)
已知函数  =
=  x3+bx2+4cx
x3+bx2+4cx 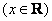 是奇函数,函数
是奇函数,函数  在点
在点 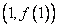 处的切线的斜率为-6, 且当x=2时,函数
处的切线的斜率为-6, 且当x=2时,函数  有极值.
有极值.
(I)求b的值;
(II)求函数  的解析式;
的解析式;
(Ⅲ)求函数  的单调区间.
的单调区间.
(17)(本小题共12分)
某区有4家不同的达美乐比萨连锁分店,有3名同学前去就餐(假设每位同学选择某店就餐失等可能的).
﹙Ⅰ﹚求这3位同学选择在同一连锁分店就餐的概率;
﹙Ⅱ﹚求这3位同学选择在三家连锁分店就餐的概率;
﹙Ⅲ﹚求这3位同学中恰有两位同学选择在同一连锁分店就餐的概率.
(18)(本小题共14分)
已知等差数列 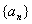 的前n项和为
的前n项和为  ,且
,且 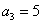 ,
, 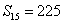 . 数列
. 数列 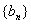 是等比数列,
是等比数列,
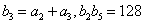 (其中
(其中 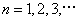 ).
).
(I)求数列 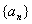 和
和  的通项公式;
的通项公式;
(II)记  .
.
(19)(本小题共14分)
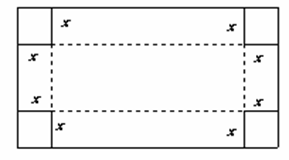
今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为  米的正方形后,沿虚线折起,做成一个无盖的长方体形水箱(接口连接问题不考虑).
米的正方形后,沿虚线折起,做成一个无盖的长方体形水箱(接口连接问题不考虑).
(I)求水箱容积的表达式  ,并指出函数
,并指出函数  的定义域;
的定义域;
 (II)若要使水箱容积不大于4 (II)若要使水箱容积不大于4 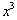 立方米的同时,又使得底面积最大,求
立方米的同时,又使得底面积最大,求  的值?
的值?
(20)(本小题共13分)
设函数 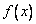 的定义域为
的定义域为 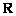 ,若
,若 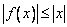 对一切实数
对一切实数  均成立,则称函数
均成立,则称函数 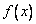 为
为 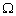 函数.
函数.
(I)求证:若函数 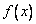 为
为 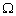 函数,则
函数,则 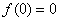 ;
;
(II)试判定函数 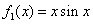 、
、 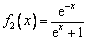 和
和  中哪些是
中哪些是 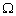 函数,并说明理由;
函数,并说明理由;
(III)若  是奇函数且是定义在R上的可导函数,函数
是奇函数且是定义在R上的可导函数,函数  的导数
的导数  满足
满足 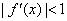 ,试判定函数
,试判定函数  是否为
是否为 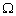 函数,并说明理由.
函数,并说明理由.
数 学(文科)试卷
一. 选择题(本大题共8小题,每小题5分,共40分) |
题号 |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) | |
答案 |
D |
B |
A |
A |
C |
C |
B |
D | |
二. 填空题(本大题共6小题,每小题5分.有两空的小题,第一空3分,第二空2分,共30分)
(9)  (10)
(10) 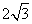 (11) 20 (12) 2
(11) 20 (12) 2
(13)  (14) 4,405
(14) 4,405
三.解答题 (本大题共6小题,共80分)
(15) (共13分)
解:﹙Ⅰ﹚由已知得: 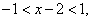 解得,
解得, 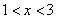 ………………. 3分
………………. 3分
∴集合 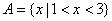 . ……………….4分
. ……………….4分
由已知得: 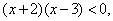 解得
解得 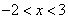 . ……………….8分
. ……………….8分
∴集合  . ………………. 9分
. ………………. 9分
﹙Ⅱ﹚由(I)可得: 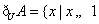 或
或 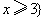 , ……………….11分
, ……………….11分
故 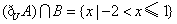 . .……………….13分
. .……………….13分
﹙16﹚(共14分)
解:(I)由函数  是奇函数,∴
是奇函数,∴  ,
, 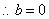 . 2分
. 2分
(II)由 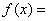
 x3+4cx,
x3+4cx,
有 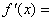 ax2+4c 且
ax2+4c 且 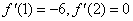 .
.
∴  解得
解得 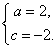 6分
6分
故 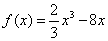 . ………………………………………………8分
. ………………………………………………8分
﹙Ⅲ﹚  f(x)=
f(x)=  x3-8x,∴
x3-8x,∴ 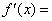 2x2-8=2(x+2)(x-2). 10分
2x2-8=2(x+2)(x-2). 10分
令  >0得x<-2或x>2 , 令
>0得x<-2或x>2 , 令  <0得-2<x<2. 12分
<0得-2<x<2. 12分
∴函数  的单调增区间为(
的单调增区间为( 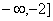 ,[2,+
,[2,+ 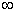
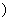 ;单调减区间为[-2,2]. 14分
;单调减区间为[-2,2]. 14分
(或增区间为 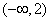 ,(2,+
,(2,+ 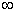
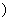 ;减区间为(-2,2))
;减区间为(-2,2))
(17)(共12分)
解:﹙Ⅰ﹚ “这3位同学选择在同一连锁分店就餐”的事件记为A,
由题意 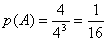 . ……………….4分
. ……………….4分
答:这3位同学选择在同一连锁分店就餐的概率为 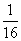 .
.
﹙Ⅱ﹚“这3位同学选择在三家连锁分店就餐”的事件记为B,
由题意 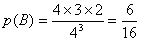
 . ……………….8分
. ……………….8分
答:这3位同学选择在三家连锁分店就餐的概率为 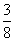 .
.
﹙Ⅲ﹚“这3位同学中恰有两位同学选择同一连锁分店就餐”的事件记为C,
由题意 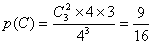 . ……………….12分
. ……………….12分
答:这3位同学中恰有两位同学选择同一连锁分店就餐的概率为 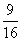 .
.
(18)( 共14分)
解(I)设等差数列 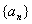 的公差为d,
的公差为d,
则 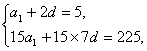 2分
2分
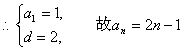
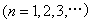 . 4分
. 4分
设等比数列 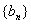 的公比为
的公比为 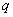 ,
,
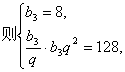
 6分
6分
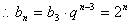
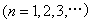 . 8分
. 8分
(II) 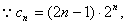
 10分
10分
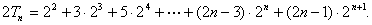
作差: 
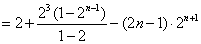

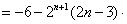 13分
13分
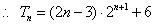
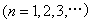 . 14分
. 14分
(19)(共14分)
解:(I)由已知该长方体形水箱高为  米,底面矩形长为(
米,底面矩形长为(  )米,宽(
)米,宽( 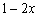 )米. 2分
)米. 2分
∴该水箱容积为 
 . 4分
. 4分
其中正数  满足
满足 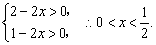
∴所求函数  定义域为
定义域为  . 7分
. 7分
(II)由  得
得 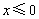 或
或 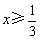 .
.
 函数
函数  定义域为
定义域为  ,
, 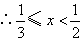 . 9分
. 9分
此时底面积为 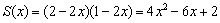
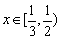 . 11分
. 11分
由 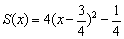 ,可知
,可知  在
在  上是减函数, 13分
上是减函数, 13分
∴ 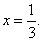 14分
14分
答:满足条件的  为
为  米.
米.
(20)(共13分)
解:(I)∵函数 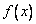 的定义域为
的定义域为 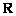 ,且
,且  ,
,
∴ 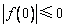 ,又
,又 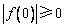 ,∴
,∴ 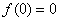 . 2分
. 2分
(II)∵ 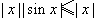 ,∴
,∴ 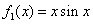 是
是  函数; 4分
函数; 4分
∵ 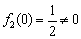 ∴
∴  不是
不是 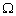 函数; 6分
函数; 6分
∵ 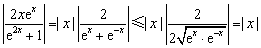 ,∴
,∴ 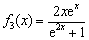 是
是 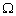 函数. 8分
函数. 8分
(III)∵函数 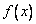 是定义在R 上的奇函数,∴
是定义在R 上的奇函数,∴ 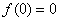 .
.
∵ 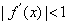 , ∴
, ∴  .
.
当  时,
时,
设函数 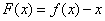 和
和  .
.
∴  ,
, 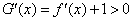 .
.
∴ 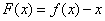 在
在 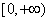 上是减函数,
上是减函数,  在
在 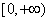 上是增函数.
上是增函数.
∴  ,
, 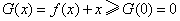 .
.
∴  . ∴当
. ∴当  时,
时, 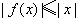 成立.
成立.
当 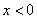 时,则
时,则 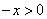 ,∴
,∴ 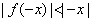 ,
,
∵  为奇函数,∴
为奇函数,∴  即
即 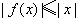 成立.
成立.
∴当  时,
时, 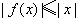 对一切实数
对一切实数 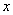 均成立.
均成立.
故函数  是
是 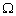 函数. 13分
函数. 13分
来源:中国哲士网
教师学生家长 数高三上末资料 备课考试教学
教育资料 [组图]高三文科数学第五次考试试题 文章
|
| 上一篇文章: 高三理科数学第一学期期末考试 |
| 下一篇文章: 高三文科数学第一学期期末考试试题 |
| |
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
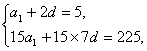
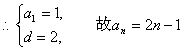
![]()
![]()
![]()
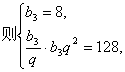
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()