|
高考数学第二次诊断性考试试卷
数 学
注重事项:
1.答选择题前,考生务必将自己的姓名、考生号、考试科目、试卷类型等写在答题纸上,并贴好条形码。
2.每小题选出答案后,用铅笔把答题纸上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案;不能答在试卷上。
3.主观题请在规定区域答题。请务必保持答题纸的整洁,不要折叠,考试结束,将答题纸交回。
一、填空题:本大题共14小题,每小题5分,共70分.把答案填写在答题卡相应位置上.
1.设集合 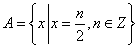 ,
, 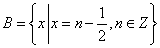 ,则
,则 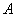 与
与 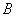 的关系是▲ .
的关系是▲ .
 2.复数 2.复数 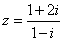 的虚部为 ▲ .
的虚部为 ▲ .
3.如图,在 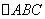 中,
中, 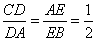 ,记
,记 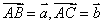 ,
,
则 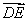 = ▲ .(用
= ▲ .(用 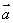 与
与 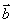 表示)
表示)
4.在数列 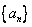 中,已知
中,已知 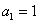 ,
, 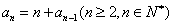 ,则
,则 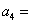 ▲ .
▲ .
5.函数 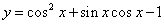 的单调减区间是___▲_____.
的单调减区间是___▲_____.
6.若关于 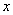 的方程
的方程 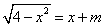 有两个不同的实数根,则实数
有两个不同的实数根,则实数 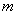 的取值范围是 ▲ .
的取值范围是 ▲ .
7.设 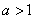 ,函数
,函数 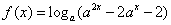 ,则使
,则使 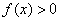 的
的 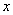 的取值范围是 ▲ .
的取值范围是 ▲ .
8.已知圆 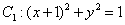 ,圆
,圆 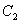 与圆
与圆 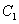 外切,且与直线
外切,且与直线 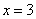 切于点
切于点 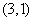 ,则圆
,则圆 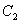 的方程为 ▲ .
的方程为 ▲ .
 9.如图,水波的半径以 9.如图,水波的半径以 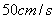 的速度向外扩张,当半径为
的速度向外扩张,当半径为 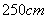 时,圆面积的膨胀率为 ▲
时,圆面积的膨胀率为 ▲ 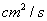 .
.
10.若函数 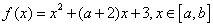 的图像关于直线
的图像关于直线 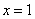 对称,
对称,
 则此 则此 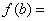 ▲ .
▲ .
11.如图,摩天轮的半径为 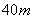 ,点
,点  距地面的高度为
距地面的高度为 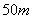 摩
摩
天轮做匀速转动,每 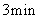 转一圈,摩天轮上点
转一圈,摩天轮上点 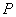 的起始位置在
的起始位置在
最低处.在摩天轮转动的一圈内,有 ▲ 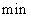
点 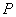 距离地面超过
距离地面超过 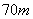 .
.
12.已知圆 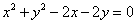 上有
上有 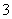 个点到直线
个点到直线 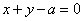 的距离都等于
的距离都等于  ,
,
则 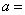 ▲ .
▲ .
13.给出以下四个命题:
①已知命题 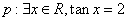 ;命题
;命题 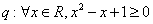 .则命题
.则命题 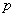 和
和 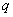 都是真命题;
都是真命题;
②过点 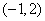 且在
且在 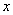 轴和
轴和  轴上的截距相等的直线方程是
轴上的截距相等的直线方程是 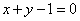 ;
;
③函数 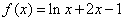 在定义域内有且只有一个零点;
在定义域内有且只有一个零点;
④先将函数 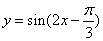 的图像向左平移
的图像向左平移 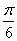 个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为
个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为 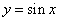 .
.
其中正确命题的序号为 ▲ .(把你认为正确的命题序号都填上)
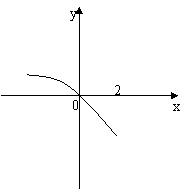 14.已知函数 14.已知函数 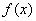 的定义域为
的定义域为 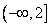 ,部分对应值如下表.
,部分对应值如下表. 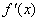 为
为 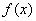 的导数,函数
的导数,函数 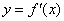 的图像如右图所示.
的图像如右图所示.
若两正实数 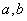 满足
满足 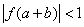 ,则
,则 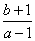 的取值范围是 ▲ .
的取值范围是 ▲ .
二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证实过程或演算步骤.
15.(本小题满分14分)已知椭圆  的右焦点
的右焦点 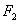 与抛物线
与抛物线 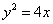 的焦点重合,且经过点
的焦点重合,且经过点 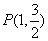 .
.
⑴求此椭圆的方程及其离心率;
⑵求以这个椭圆的焦点为顶点、顶点为焦点的双曲线的方程.
16.(本小题满分14分)已知向量 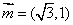 ,向量
,向量 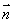 是与向量
是与向量 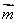 夹角为
夹角为 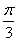 的单位向量.
的单位向量.
⑴求向量 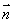 ;
;
⑵若向量 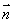 与向量
与向量 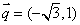 共线,与向量
共线,与向量 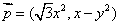 垂直,求
垂直,求 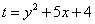 的最大值.
的最大值.
17.(本小题满分15分)设数列 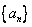 的各项均为正数,它的前
的各项均为正数,它的前 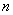 项的和为
项的和为 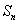 ,点
,点 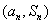 在函数
在函数 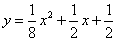 的图像上;数列
的图像上;数列 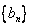 满足
满足 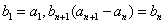 .其中
.其中 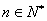 .
.
⑴求数列 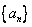 和
和 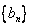 的通项公式;
的通项公式;
⑵设  ,求证:数列
,求证:数列 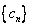 的前
的前 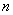 项的和
项的和 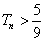 (
( 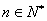 ).
).
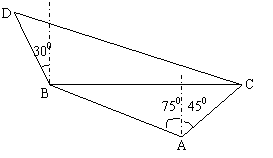
18.(本小题满分15分)在海岸 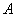 处,发现北偏西
处,发现北偏西 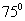 的方向,距离
的方向,距离 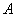
 mile的
mile的 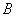 处有一艘走私船,在
处有一艘走私船,在 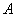 处北偏东
处北偏东  方向,距离
方向,距离 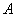
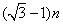 mile的
mile的 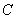 处的缉私船奉命以
处的缉私船奉命以 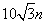 mile/h的速度追截走私船.此时,走私船正以
mile/h的速度追截走私船.此时,走私船正以 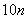 mile/h的速度从
mile/h的速度从 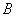 向北偏西
向北偏西 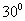 方向逃窜,问缉私船沿什么方向能最快追上走私船?
方向逃窜,问缉私船沿什么方向能最快追上走私船?
19.(本小题满分16分)已知函数 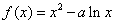 和
和 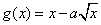 在
在 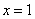 处的切线平行.
处的切线平行.
⑴试求函数 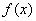 和
和 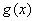 的单调增区间;
的单调增区间;
⑵设 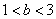 ,求证:
,求证: 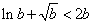 .
.
20.(本小题满分16分)定义在正整数集上的函数 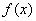 对任意
对任意 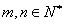 ,都有
,都有
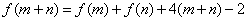 ,且
,且 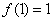 .
.
⑴求函数 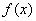 的表达式;
的表达式;
⑵若 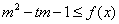 对于任意的
对于任意的 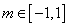 、
、 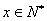 恒成立,求实数
恒成立,求实数 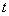 的取值范围;
的取值范围;
⑶对任意正整数 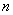 ,在
,在 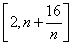 内总存在
内总存在 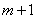 个实数
个实数 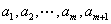 ,
,
使 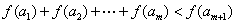 成立,求
成立,求 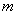 的最大值.
的最大值.
08届高考数学第二次诊断性考试试卷
数学附加题
1.(本小题满分8分)求曲线 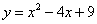 及直线
及直线 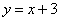 所围封闭区域的面积.
所围封闭区域的面积.
2.(本小题满分10分)求直线 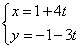 (
( 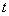 为参数)被曲线
为参数)被曲线 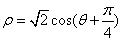 所截得的弦长.
所截得的弦长.
3.(本小题满分10分)设 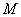 是把坐标平面上的点的横坐标伸长到
是把坐标平面上的点的横坐标伸长到 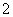 倍,纵坐标伸长到
倍,纵坐标伸长到 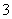 倍的伸压变换.
倍的伸压变换.
(1)求矩阵 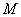 的特征值及相应的特征向量;
的特征值及相应的特征向量;
(2)求逆矩阵 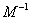 以及椭圆
以及椭圆 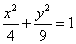 在
在 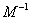 的作用下的新曲线的方程.
的作用下的新曲线的方程.
4.(本小题满分12分)假定某射手每次射击命中的概率为 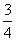 ,且只有
,且只有 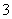 发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为
发子弹.该射手一旦射中目标,就停止射击,否则就一直独立地射击到子弹用完.设耗用子弹数为 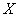 ,求:
,求:
⑴目标被击中的概率;
⑵ 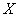 的概率分布;
的概率分布;
⑶均值 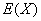 .
.
08届高考数学第二次诊断性考试试卷
高三数学参考答案
1. 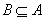 或
或 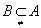 2.
2. 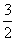 3.
3. 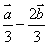 4.
4. 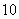 5.
5. 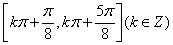 6.
6. 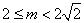 7.
7. 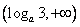 8.
8. 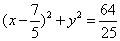 9.
9. 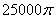 10.
10. 
11.  12.
12.  或
或 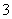 13.①③④ 14.
13.①③④ 14. 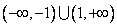
15.⑴由条件得 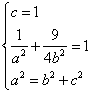
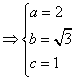
∴所求的椭圆的方程为 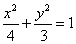 ,
,
其离心率 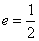 ;
;
⑵由条件得,双曲线的半焦距 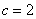 ,实半轴长
,实半轴长 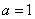 ,所以
,所以 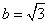 ,又因为此双曲线的焦点在
,又因为此双曲线的焦点在 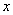 轴上,中心在原点,所以双曲线的方程为
轴上,中心在原点,所以双曲线的方程为 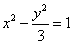 .
.
16.⑴设向量  ,则
,则 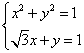 ,
,
解之得: 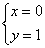 或
或 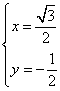 ,
,
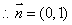 或
或 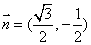 ;
;
⑵∵向量 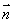 与向量
与向量 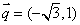 共线,∴
共线,∴ 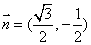 ,
,
又∵与向量 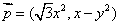 垂直,
垂直,
∴ 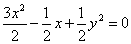 ,即
,即 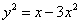
∴ 
由  ,可得
,可得 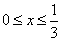 ,
,
∴当 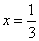 时,
时, 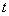 取得最大值,最大值为
取得最大值,最大值为 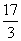 .
.
17. ⑴由已知条件得 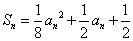 , ①
, ①
当 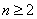 时,
时, 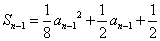 , ②
, ②
①-②得: 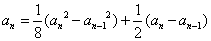 ,即
,即 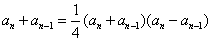 ,
,
∵数列 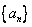 的各项均为正数,∴
的各项均为正数,∴ 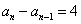 (
( 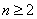 ),
),
又  ,∴
,∴ 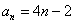 ;
;
∵ 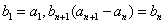 ,
,
∴ 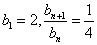 ,∴
,∴ 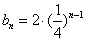 ;
;
⑵∵ 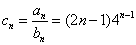 ,
,
∴ 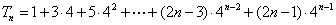 ,
,
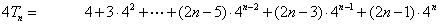 ,
,
两式相减得 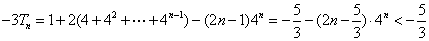 ,
,
∴ 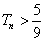 .
.
18. 由已知条件得, 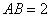 ,
, 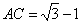 ,
, 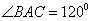 ,
,
∴ 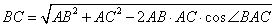
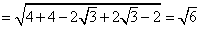 ,
,
在 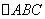 中,
中, 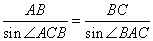 ,解之得
,解之得 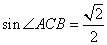 ,
,
∴  ,∴
,∴ 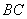 为水平线,
为水平线,
设经过时间 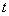 小时后,缉私船追上走私船,
小时后,缉私船追上走私船,
则在 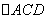 中,
中, 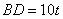 ,
, 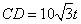 ,
, 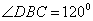 ,
,
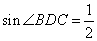 ,∴
,∴ 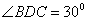 ,
,
∴缉私船沿北偏西 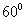 的方向能最快追上走私船.
的方向能最快追上走私船.
19.⑴∵ 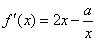 ,
, 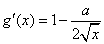 ,
,
由条件得 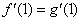 ,即
,即 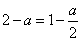 ,解得
,解得 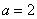 ,
,
令 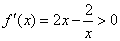 ,解得
,解得 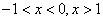 ,而
,而 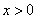 ,
,
∴函数 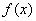 的单调增区间为
的单调增区间为 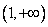 ,
,
同理 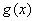 的单调增区间为
的单调增区间为 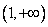 ;
;
⑵∵函数 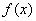 在
在 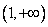 上是增函数,且
上是增函数,且 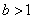 ,
,
∴ 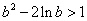 ,
,
同理 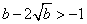 ,
,
∴ 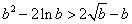 ,
,
∵ 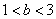 ,∴
,∴ 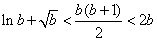 ,即
,即 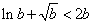 .
.
20.⑴取 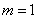 ,
,  ,
,
当 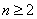 时,
时, 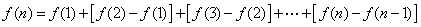
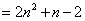 ,
,
又 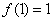 ,∴
,∴ 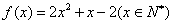 ;
;
⑵  ,
,
∴ 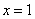 时
时 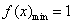 ,
,
由条件得 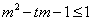 在
在 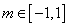 上恒成立,即
上恒成立,即 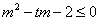 ,
,
若  ,则
,则 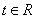 ,
,
若 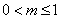 ,则
,则 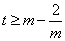 ,即
,即 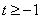 ,
,
若 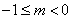 ,则
,则 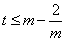 ,即
,即 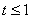 ,
,
综上: 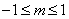 ;
;
⑶∵ 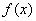 在
在 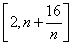 上单调递增,
上单调递增,
∴ 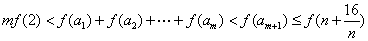
∴只须 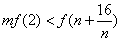 对
对 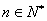 恒成立,
恒成立,
而 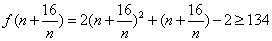 ,
,
∴ 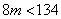 即
即 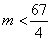 ,又
,又 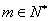 ,
,
∴ 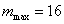 .
.
附加题答案:
1.解方程组 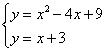 ,得
,得 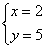 或
或 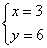 ,
,
∴面积 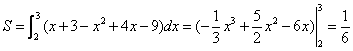 .
.
2.把 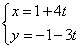 化为普通方程为
化为普通方程为 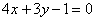 ,
,
把 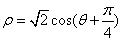 化为直角坐标系中的方程为
化为直角坐标系中的方程为 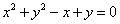 ,
,
∴圆心到直线的距离为  ,
,
∴弦长为 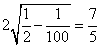 .
.
3.(1)由条件得矩阵 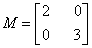 ,
,
它的特征值为 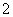 和
和 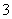 ,对应的特征向量为
,对应的特征向量为 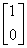 及
及 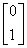 ;
;
(2) 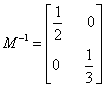 ,
,
椭圆 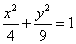 在
在 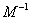 的作用下的新曲线的方程为
的作用下的新曲线的方程为 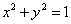 .
.
4. ⑴目标被击中的概率为 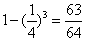 ;
;
⑵ 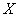 的分布列为
的分布列为
⑶均值 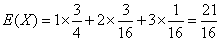 .
.
|