|
高考数学三月综合测试
理科数学试卷
命题人:徐喜峰(2008年03月17日)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷50分,第Ⅱ卷100分,卷面共计150分,时间120分钟.
第Ⅰ卷(选择题 共50分)
注重事项:
1.答第Ⅰ卷前,考生务必将自己的考号、班级、姓名等用钢笔或圆珠笔填写在答题卷上.
2.每小题选出答案后,用钢笔或圆珠笔填写在答题卷上.
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共12小题,每小题5分,共60分)
1.若全集U = R,集合 
A. 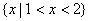 B.
B. 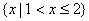 C.
C.  D.
D. 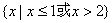
2.向量 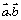 满足
满足 
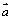 与
与 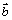 的夹角为60°,则
的夹角为60°,则 
A.1 B.  C.
C.  D.
D. 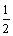
3. 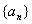 为等差数列,若
为等差数列,若  ,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n =
,且它的前n项和Sn有最小值,那么当Sn取得最小正值时,n =
A.11 B.17 C.19 D.21
4.不等式 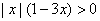 的解集是
的解集是
A. 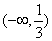 B.
B. 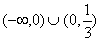 C.
C. 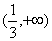 D.(0,
D.(0, 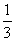 )
)
5.设 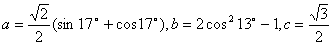 ,则
,则
A. 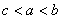 B.
B.  C.
C. 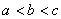 D.
D. 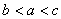
6.在 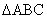 中,已知sinC=2sin(B C)cosB,那么
中,已知sinC=2sin(B C)cosB,那么 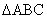 一定是
一定是
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
7.随机变量ξ的概率分布规律为P(ξ=n)=eq \f(a,n(n+1))(n=1,2,3,4),其中a是常数,则P(eq \f(1,2)<ξ<eq \f(5,2))的值为
A.eq \f(2,3) B.eq \f(3,4) C.eq \f(4,5) D.eq \f(5,6)
8.在正项等差数列{an}中,前n项和为Sn,在正项等比数列{bn}中,前n项和为Tn,若a15=b5,a30=b20,则eq \f(S30-S15,T20-T5)∈( )
A.(0,1) B.(eq \f(1,2),1) C.[1,+∞] D.[eq \f(1,2),2]
9.正三棱锥P—ABC的三条侧棱两两互相垂直,则该正三棱锥的内切球与外接球的半径之比为
A.1:3 B. 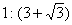 C.
C. 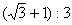 D.
D. 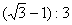
10.已知P是椭圆  上的点,F1、F2分别是椭圆的左、右焦点,若
上的点,F1、F2分别是椭圆的左、右焦点,若 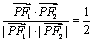 ,则△F1PF2的面积为
,则△F1PF2的面积为
A. 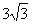 B.
B. 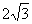 C.
C. 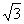 D.
D. 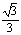
第Ⅱ卷(非选择题 共100分)
二、填空题:把答案填在答题卡相应题号后的横线上(本大题共5小题,每小题5分,共25分)
11.已知等式 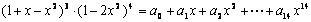 成立,则
成立,则 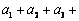
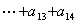 的值等于 .
的值等于 .
12.直线  和圆
和圆 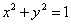 交于点A、B,以
交于点A、B,以 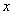 轴的正方向为始边,OA为终边(O是坐标原点)的角为
轴的正方向为始边,OA为终边(O是坐标原点)的角为 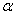 ,OB为终边的角为
,OB为终边的角为 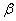 ,那么
,那么 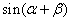 是 .
是 .
13.已知 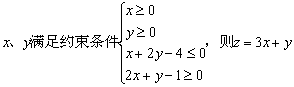 的最小值是 .
的最小值是 .
14.抛物线y=(n2+n)x2-(2n+1)x+1(n∈N+),交x轴于An,Bn两点,则|A1B1|+|A2B2|+…+|A2007B2007|的值为
15.下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥;
②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥;
③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥;
④侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥.
其中真命题的编号是_____________
三、解答题:解答应写出文字说明,证实过程或演算步骤(本大题共6小题,共75分)
16.(本小题满分12分)
已知锐角三角形△ABC中,角A、B、C的对边分别为 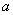 、
、 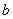 、
、  ,
, 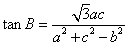 。
。
(Ⅰ)求角B的大小;
(Ⅱ)求 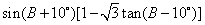 的值。
的值。
17.(本小题满分12分)
甲、乙、丙、丁四人做相互传球练习,第一次甲传给其他三人中的一人,第二次由拿球者再传给其他
三人中的一人,……,且拿球者传给其他三人中的任何一人都是等可能的,求:
(Ⅰ)共传了四次,第四次球传回到甲的概率;
(Ⅱ)若规定:最多传五次球,且在传球过程中,球传回到甲手中即停止传球;设ξ表示传球停止时传
球的次数,求 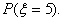
18.(本小题满分12分)
在四棱锥P—ABCD中,底面ABCD是a的正方形,
PA⊥平面ABCD,且PA=2AB
(Ⅰ)求证:平面PAC⊥平面PBD;
(Ⅱ)求二面角B—PC—D的余弦值.
19.(本小题满分12分)
若函数 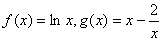
(Ⅰ)求函数 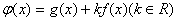 的单调区间
的单调区间
(Ⅱ)若对所有的 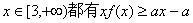 成立,求实数a的取值范围.
成立,求实数a的取值范围.
20.(本小题满分13分)
已知直线 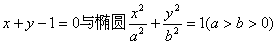 相交于A、B两点,M是线段AB上的一点,
相交于A、B两点,M是线段AB上的一点, 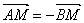 ,且点M在直线
,且点M在直线 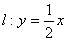 上.
上.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若椭圆的焦点关于直线l的对称点在单位圆  上,求椭圆的方程.
上,求椭圆的方程.
21.(本小题满分14分)
把正奇数数列 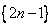 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
- - - -
- - - - -
设 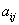 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第  行,从左往右数第
行,从左往右数第 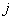 个数。
个数。
(Ⅰ)若 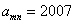 ,求
,求 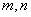 的值;
的值;
(Ⅱ)已知函数 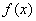 的反函数
的反函数  为,若记三角形数表中从上往下数第
为,若记三角形数表中从上往下数第 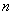 行各数的和为
行各数的和为  ,求数列
,求数列 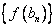 的前
的前 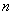 项和
项和 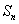 。
。
理科参考答案
一、选择题:
DDCBA BDCDA
二、填空题:
11.0 12. 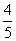 13.1 14.
13.1 14. 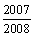 15. ①④
15. ①④
三、解答题:
16.解:(Ⅰ)  ;(Ⅱ)
;(Ⅱ) 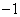 12分
12分
17.解:(Ⅰ) 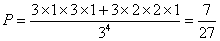 6分
6分
(Ⅱ) 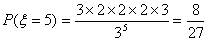 12分
12分
18.解:(Ⅰ)证实:∵PA⊥平面ABCD ∴PA⊥BD
∵ABCD为正方形 ∴AC⊥BD
∴BD⊥平面PAC又BD在平面BPD内,
∴平面PAC⊥平面BPD 6分
(Ⅱ)解法一:在平面BCP内作BN⊥PC垂足为N,连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B—PC—D的平面角,
在△BND中,BN=DN= 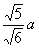 ,BD=
,BD= 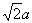
∴cos∠BND = 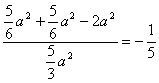 12分
12分
解法二:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立空间坐标系如图,在平面BCP内作BN⊥PC垂足为N连DN,
∵Rt△PBC≌Rt△PDC,由BN⊥PC得DN⊥PC;
∴∠BND为二面角B—PC—D的平面角 8分
设 
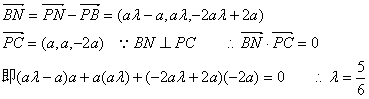
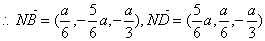 10分
10分
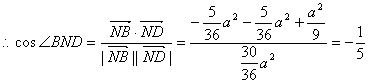 12分
12分
解法三:以A为原点,AB、AD、AP所在直线分别为x轴、y轴、z轴建立如图空间坐标系,作AM⊥PB于M、AN⊥PD于N,易证AM⊥平面PBC,AN⊥平面PDC,
设 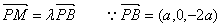
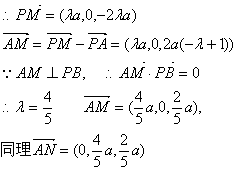
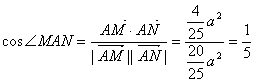 10分
10分
∵二面角B—PC—D的平面角与∠MAN互补
∴二面角B—PC—D的余弦值为 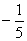 12分
12分
19.解:(1) 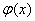 的定义域为
的定义域为 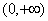 …………12分
…………12分
 …………2分
…………2分
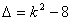
①当 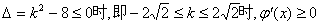 …………3分
…………3分
②  时
时
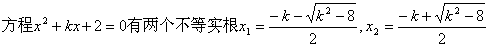
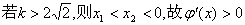 …………4分
…………4分
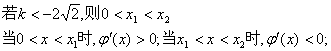
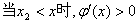 …………5分
…………5分
综上:

单调递减区间为 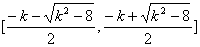
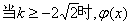 的单调递增区间(0,
的单调递增区间(0, 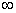 ) …………6分
) …………6分
(2) 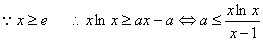 …………7分
…………7分
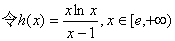 …………8分
…………8分
则 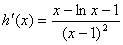 …………9分
…………9分
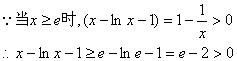
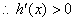 …………10分
…………10分
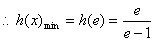 …………11分
…………11分
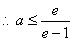 …………12分
…………12分
另解: 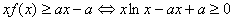
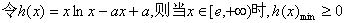 …………7分
…………7分
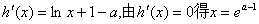 …………8分
…………8分
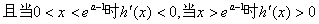
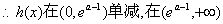 单增 …………9分
单增 …………9分
①当 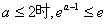
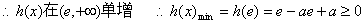
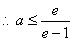 …………11分
…………11分
②当 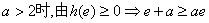
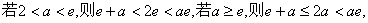
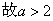 不成立 …………12分
不成立 …………12分
综上所述 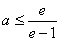
20.解:(Ⅰ)由 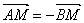 知M是AB的中点,
知M是AB的中点,
设A、B两点的坐标分别为 
由 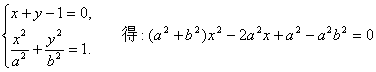
 ,
,
∴M点的坐标为 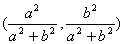 4分
4分
又M点的直线l上: 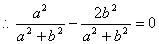

 7分
7分
(Ⅱ)由(Ⅰ)知  ,不妨设椭圆的一个焦点坐标为
,不妨设椭圆的一个焦点坐标为  关于直线l:
关于直线l:
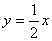 上的对称点为
上的对称点为 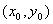 ,
,
则有 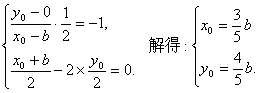 10分
10分
由已知 
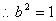 ,∴所求的椭圆的方程为
,∴所求的椭圆的方程为  12分
12分
21.解:(Ⅰ)∵三角形数表中前 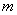 行共有
行共有 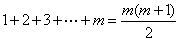 个数,
个数,
∴第 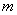 行最后一个数应当是所给奇数列中第
行最后一个数应当是所给奇数列中第 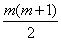 项,即
项,即 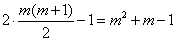 。
。
因此,使得 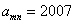 的
的 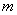 是不等式
是不等式  的最小正整数解。
的最小正整数解。
由  得
得 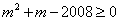 ,∴
,∴ 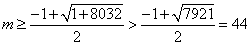 。∴
。∴ 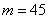 。
。
第45行第一个数是 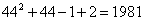 ,∴
,∴ 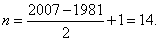
(Ⅱ)∵  ,∴
,∴ 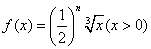 。
。
∵第 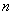 行最后一个数是
行最后一个数是 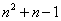 ,且有
,且有 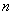 个数,若
个数,若 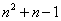 将看成第
将看成第 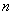 行第一个数,则第
行第一个数,则第 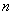 行各数成公差为
行各数成公差为 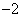 的等差数列,故
的等差数列,故 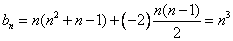 。∴
。∴  。
。
故 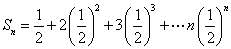 。用错位相减法可求得
。用错位相减法可求得 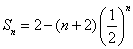 。
。
|