|
高考数学平面向量的综合应用测试题
姓名_______班级_______得分________
1.已知点M1(6,2)和M2(1,7),直线y=mx-7与线段M1M2的交点分有向线段M1M2的比为3:2,则的值为 ( )
A. 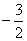 B.
B. 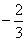 C.
C. 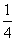 D.4
D.4
2.已知a,b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是 ( )
A. 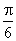 B.
B.  C.
C. 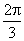 D.
D. 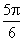
3.已知向量 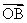 =(2,0),向量
=(2,0),向量 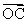 =(2,2),向量
=(2,2),向量 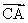 =(
=( 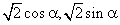 ),则向量
),则向量  与向量
与向量 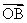 的夹角的范围为 ( )
的夹角的范围为 ( )
A.[0,  ] B.[
] B.[  ,
, 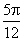 ] C.[
] C.[ 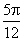 ,
,  ] D.[
] D.[  ,
, 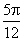 ]
]
4.设坐标原点为O,抛物线y2=2x与过焦点的直线交于A,B两点,则  ·
· 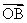 = ( )
= ( )
A.  B.
B. 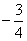 C.3 D.-3
C.3 D.-3
5.O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满足 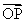 =
=  λ(
λ( 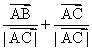 ),
), 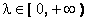 ,则点P的轨迹一定通过△ABC的 ( )
,则点P的轨迹一定通过△ABC的 ( )
A.外心 B.内心 C.重心 D.垂心
6.已知平面上直线l的方向向量e=( 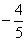 ,
, 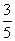 ),点O(0,0)和A(1, -2)在上的射影分别是O/和A/,则
),点O(0,0)和A(1, -2)在上的射影分别是O/和A/,则  ,其中λ= ( )
,其中λ= ( )
A. 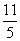 B.
B. 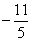 C.2 D.-2
C.2 D.-2
7.已知向量a=( 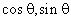 ),向量b=(
),向量b=(  ),则|2a-b|的最大值是
),则|2a-b|的最大值是
8.把函数y=2x2-4x+5的图像按向量a平移,得到y=2x2的图像,且a⊥b,c=(1,-1),b·c=4,则b=
9.已知向量 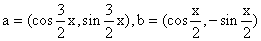 ,且x∈[0,
,且x∈[0,  ],求
],求
(1)a·b及|a b|;
(2)若 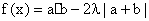 的最小值是
的最小值是 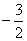 ,求实数
,求实数 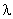 的值。
的值。
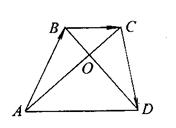 10.如图, 10.如图,  ,
,
(1)若 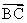 ∥
∥ 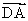 ,求x与y间的关系;
,求x与y间的关系;
(2)若有 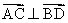 ,求x,y的值及四边形ABCD的面积.
,求x,y的值及四边形ABCD的面积.
11.已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP至点N,且  。
。
(1)求动点N的轨迹方程;
(2)直线l与动点N的轨迹交于A、B两点,若  且4
且4 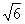 ≤
≤ 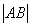 ≤
≤  ,求直线l的斜率的取值范围。
,求直线l的斜率的取值范围。
答案:
1. D 2. B 3. D 4. B 5. B 6. D 7. 4 8. (3, -1)
9. 略解:(1) 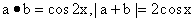
(2) 
分λ<0, 0≤λ≤1, λ>1讨论,得 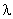 =
= 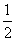
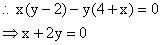 10. 略解(1) 10. 略解(1) 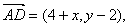 又
又  ∥
∥ 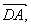 (2)由
(2)由 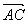 ⊥
⊥ 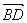 ,得
,得
(x-2)(6+x)+(y-3)·(y+1)=0, 即 x2+y2+4x-2y-15=0 ②
  x=-6 x=2 x=-6 x=2
由①,②得 或, 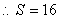
y =3 y=-1
11. 略解 (1)y2=4x (x>0)
(2)先证实l与x轴不垂直,再设l的方程为y=kx+b(k≠0),A(x1,y1),B(x2,y2).联立直线与抛物线方程,得ky2- 4y+4b=0,由  ,得
,得  .又
.又 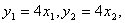 故
故  而
而 
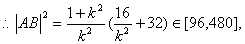 解得直线l的斜率的取值范围是
解得直线l的斜率的取值范围是 
|