|
1、如图,点A、B、C都在⊙O上,且点C在弦AB所对的优弧上,若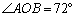 ,则 ,则 的度数 的度数
是( )
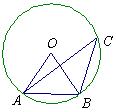
A.18° B.30° C.36° D.72°
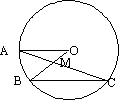
2、如图,在⊙O中,弦BC//半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
A.30° B.60° C.50° D.40°
3、如图,⊙O的直径是AB,CD是⊙O的弦,若∠D=70°,则∠ABC等于___________.
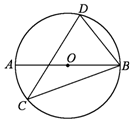
4、如图,AB是⊙O的弦,∠AOB = 130°,点C为AB弧的中点,则∠CAB =___________.
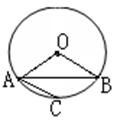
5、如图,量角器外沿上有A、B两点,它们的读数分别是70°、40°,则∠1的度数为___________.
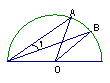
6、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4. 则⊙O的直径=___________.
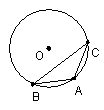
7、如图, 是 是 的直径,弦 的直径,弦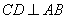 .如果 .如果 , ,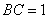 ,那么 ,那么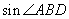 的值是___. 的值是___.
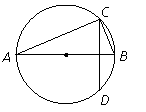
8、如图,已知 是半圆 是半圆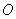 的直径,弦 的直径,弦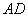 、 、 相交于点 相交于点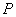 ,若 ,若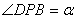 ,那么 ,那么 等于( ) 等于( )

A. B. B. C. C.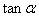 D. D.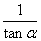
9、如图,锐角 内接于⊙O,若⊙O的半径为6,sin∠A= 内接于⊙O,若⊙O的半径为6,sin∠A=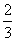 ,则BC的长为__________. ,则BC的长为__________.
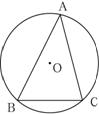
10、已知:如图,⊙O的直径AB垂直于弦CD,垂足为G,F是CD延长线上的一点,AF交⊙O于点E,连结CE.若CF=10, ,求CE的长. ,求CE的长.
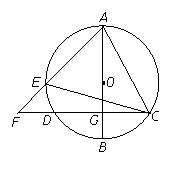
11、如图,在⊙O的内接△ABC中,AB+AC=12,AD⊥BC于D,且AD=3, 设⊙O的半径为y,AB的长为x; ①求y与x的函数解析式;
②当AB的长为多少时?⊙O的面积最大,并求出⊙O的最大面积。

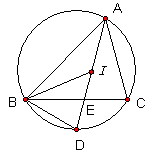
12、如图,已知点I是△ABC的∠A、∠B平分线的交点,射线AI交△ABC的外接圆于D,交BC于E。(1)试判断ID和BD的大小关系。
(2)设△ABC外接圆半径R=3,ID=2,AD=x,DE=y,当点A在优弧BC上运动时,求函数y与自变量x之间的函数关系式,并指出自变量的取值范围。
参考答案
1.C 2. B 3. 20° 4.32.5° 5.15° 6.8 7. 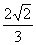 8. B 9. 8 8. B 9. 8
10.证明:∵直径AB垂直于弦CD,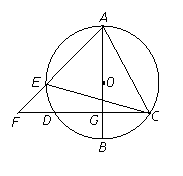
∴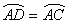
∴∠ACF=∠AEC
∵∠EAC=∠CAF
∴△AEC∽△ACF
∴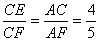
∵CF=10 ,
∴CE=8.
11.解:(1)过O作OE⊥AB于E,连结OA
则∠AOE=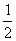 ∠A0B=∠C , AE= ∠A0B=∠C , AE=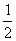 AB= AB=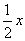
 ∵AD⊥BC ∵AD⊥BC
∴∠AEO=∠ADC=90°
∴△AOE∽△ACD
∴
∵AB+AC=12,
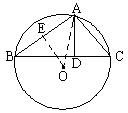
∴AC=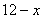
∴
∴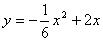 . .
(2)∵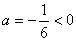 ,∴当 ,∴当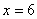 时, 时,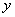 有最大值为6 有最大值为6
即当AB的长为6时,⊙O的面积最大,最大值为36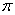 . .
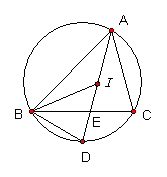 12.解:(1)∵I是△ABC的∠A、∠B平分线的交点, 12.解:(1)∵I是△ABC的∠A、∠B平分线的交点,
∴∠ABI=∠IBE , ∠BAD=∠DAC
∴
∴∠BAD=∠CBD
∵∠BID=∠BAD+∠ABI , ∠IBD=∠CBD+∠IBE
∴∠BID=∠IBD
∴BD=ID.
(2)∵∠BAD=∠CBD, ∠D=∠D
∴△ABD∽△BED
∴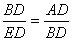
∵BD=ID=2, AD=x,DE=y,
∴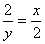
∴
∵△ABC外接圆半径R=3,
∴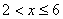 . .
|