|
一、和差倍分问题
线段或角的和差倍分问题,一般是通过平移、轴对称或旋转等变换构造全等代换线段,最终转化为证明相等的问题。
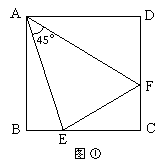
 1.如图①,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45 °,则有结论EF=BE+FD成立; 1.如图①,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45 °,则有结论EF=BE+FD成立;
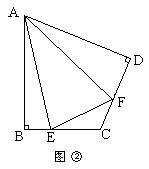
(1)如图②,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC、CD上的点,且∠EAF是∠BAD的
一半,那么结论EF=BE+FD是否仍然成立?若成立,请证明;若不成立,请说明理由;
(2)若将(1)中的条件改为:在四边形ABCD中,AB=AD,∠B+∠D=180°,延长BC到点E,延长CD到点
F,使得∠EAF仍然是∠BAD的一半,则结论EF=BE+FD是否仍然成立?若成立,请证明;若不成立,
请写出它们之间的数量关系,并证明.
解:(1)结论EF= BE+FD成立. 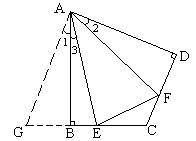
延长EB到G,使BG=DF,连接AG.
∵∠ABG=∠D=90°, AB=AD,
∴△ABG≌△ADF.
∴AG=AF且∠1=∠2.
∴∠1+∠3=∠2+∠3=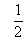 ∠BAD. ∠BAD.
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF.∴EG=EF.
即EF=BE+BG=BE+FD.
(2)结论EF=BE+FD不成立,
应当是EF=BE-FD. 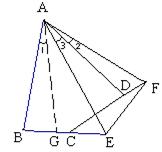
在BE上截取BG,使BG=DF,连接AG.
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF.
∵AB=AD,
∴△ABG≌△ADF.∴AG=AF.
∵∠1=∠2,
∴∠1+∠3=∠2+∠3=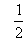 ∠BAD. ∠BAD.
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF.∴EG=EF
即EF=BE-BG=BE-FD.
此题可有如下变式:
 2.设E、F分别在正方形ABCD的边BC,CD上滑动保持且 2.设E、F分别在正方形ABCD的边BC,CD上滑动保持且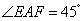 ,AP ,AP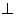 EF于点P. EF于点P.
(1)求证:AP=AB;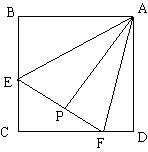
(2)若AB=5,求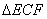 的周长。 的周长。
解:(1)将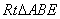 绕点A按逆时针方向旋转 绕点A按逆时针方向旋转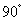 ,得 ,得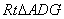
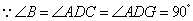 , ,
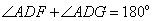 ,即F、D、G在一条直线上. ,即F、D、G在一条直线上.
 AE=AG,AF=AF, AE=AG,AF=AF,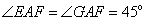 , ,
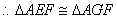 . .
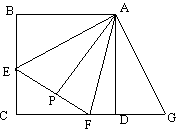
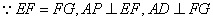 , ,
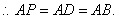
即AP=AB.
(2) 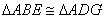 ,EF=FG. ,EF=FG.
 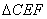 的周长=CE+EF+CF=CE+FG+CF, DG=BE, 的周长=CE+EF+CF=CE+FG+CF, DG=BE,
 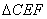 的周长=CE+EF+CF =BC+DC=5 的周长=CE+EF+CF =BC+DC=5 2 =10. 2 =10.
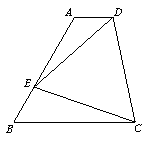  3.如图,在四边形ABCD中,AD∥BC,点E是AB上一个动点,若∠B=60°,AB=BC,且∠DEC=60°,确定AD+AE与BC的关系 3.如图,在四边形ABCD中,AD∥BC,点E是AB上一个动点,若∠B=60°,AB=BC,且∠DEC=60°,确定AD+AE与BC的关系
解: 有BC=AD+AE.
连结AC,过E作EF∥BC交AC于F点.
则可证 △AEF为等边三角形.
即 AE=EF及∠AEF=∠AFE=60°.
所以 ∠CFE=120°.
又 AD∥BC,∠B=60°,
故 ∠BAD=120°.
又 ∠DEC=60°,
所以 ∠AED=∠FEC.
在△ADE与△FCE中,
∠EAD=∠CFE,AE=EF,∠AED=∠FEC,
所以 △ADE≌△FCE. 所以 AD=FC.
则 BC=AD+AE.
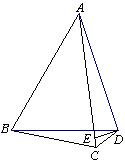  4.如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD 与AC之间有怎样的数量关系?并证明你的结论. 4.如图,四边形ABCD中,AC、BD是对角线,AB=AC,∠ABD=60°,过D作ED⊥AD,交AC于点E,恰有DE平分∠BDC.试判断线段CD、BD 与AC之间有怎样的数量关系?并证明你的结论.
结论:AC=BD+CD.
证法一:延长BD至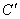 ,使得D ,使得D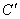 =DC. =DC.
∵DE平分∠BDC,∴∠1=∠2.
∵ED⊥AD,
∴∠ADC=90°+∠1,∠3=90°-∠2.
∵∠AD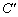 =180°-∠3=90°+∠2. =180°-∠3=90°+∠2.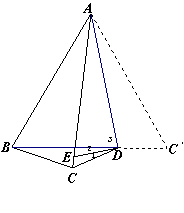
∴∠ADC=∠AD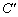 . .
在△ADC和△AD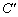 中, 中,
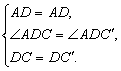
∴△ADC≌△AD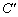 (SAS). (SAS).
∴ AC=A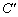 . .
∵ AB=AC,∴ AB= A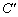 . .
∵∠ABD=60°,∴△AB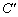 是等边三角形. 是等边三角形.
∴ A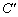 =B =B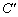 ,∴ AC =BD+CD. ,∴ AC =BD+CD.
证法二:延长CD至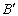 ,使D ,使D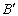 =DB. =DB.
∵ED⊥AD,
∴∠2+∠3=90°,∠1+∠4=90°.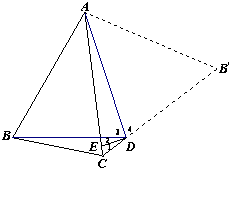
∵DE平分∠BDC,
∴∠1=∠2.
∴∠3=∠4.
在△ADB和△AD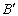 中, 中,
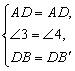
∴ △ADB≌△AD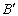 (SAS). (SAS).
∴ AB=A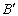 ,∠ABD=∠ ,∠ABD=∠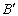 =60°. =60°.
∴ AC = A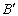 . ∴ △AC . ∴ △AC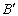 是等边三角形. 是等边三角形.
∴ AC = C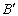 . ∴ AC =BD+CD. . ∴ AC =BD+CD.
 5.我们给出如下定义:若一个四边形中存在一组对边的平方和等于另一组对边的平方和,则称这个四边形为等平方和四边形. 5.我们给出如下定义:若一个四边形中存在一组对边的平方和等于另一组对边的平方和,则称这个四边形为等平方和四边形.
(1)写出一个你所学过的特殊四边形中是等平方和四边形的图形的名称:___________.
(2)如图(1),在梯形ABCD中,AD∥BC,AC⊥BD,垂足为O.
求证: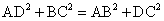 ,即四边形ABCD是等平方和四边形. ,即四边形ABCD是等平方和四边形.
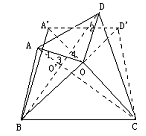
(3)如果将图(1)中的△AOD绕点O按逆时针方向旋转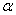 度(0°< 度(0°<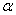 <90°)后得到图(2),那么四边形 <90°)后得到图(2),那么四边形
ABCD能否成为等平方和四边形?若能,请你证明;若不能,请说明理由.
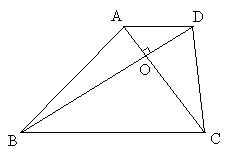 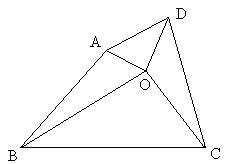
图(1) 图(2)
解:(1)菱形或正方形;
(2)证:∵AC⊥BD于点O,∴∠AOD=∠BOC=∠AOB=∠DOC=90°.
∴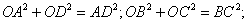
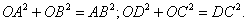
∴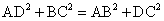 . .
即四边形ABCD是等平方和四边形.
(3)解:四边形 ABCD是等平方和四边形.
证:原梯形记为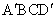 ,依题意旋转后得四边形ABCD, ,依题意旋转后得四边形ABCD,
连接AC、BD交于点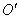 ,∵ ,∵ 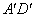 ∥BC, ∥BC,
 ∴ ∴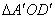 ∽ ∽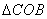 . .
∴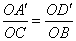 . .
∵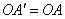 , ,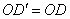 , ,
∴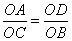 . .
∵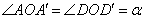 , ,
∴∠AOC=∠DOB=180°-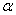 . .
又∵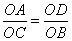 , ,
∴△AOC∽△DOB.
∴∠1=∠2.
又∵∠3=∠4,
∴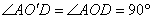 . .
由(2)的结论得: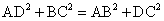 . .
即四边形ABCD是等平方和四边形.
二、位置关系的证明
位置关系的证明以线段的平行、垂直为主,对于这类问题的解决方法,大家也要注意总结归纳。比如证明垂直的方法除了利用角度推导外,还可以考虑勾股定理的逆定理、等腰三角形三线合一、三角形中一边中线等于这边一半等方法;平行证明除了利用同位角、内错角、同旁内角的关系外,还可利用中位线定理、对应线段成比例得出平行等方法。
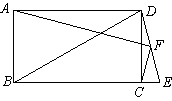  6.已知:如图,矩形ABCD中,延长BC至E点,使BE=BD,连结DE,若F是DE的中点.试确定线段AF与CF的位置关系. 6.已知:如图,矩形ABCD中,延长BC至E点,使BE=BD,连结DE,若F是DE的中点.试确定线段AF与CF的位置关系.
解:AF⊥CF
[一]连BF,易证△ADF≌BCF(SAS)
∴∠DFA=∠CFB
∴∠BFA+∠CFB=∠BFA+∠DFA=90°
[二]连AC交BD于O,连OF
∴OF为△DBE的中位线
∴OF=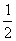 BE= BE=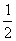 BD= BD=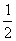 AC. AC.
 7.在△ABC中,BM、CN分别是 7.在△ABC中,BM、CN分别是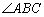 、 、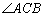 的平分线,而 的平分线,而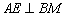 于E, 于E,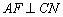 于F. 于F.
求证:EF//BC.
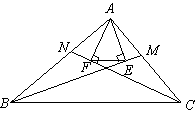 证明:延长AF交BC于D,延长AE交BC于G 证明:延长AF交BC于D,延长AE交BC于G
易证:△CAF≌△CFD
∴AF=FD
同理可证AE=EG
∴EF为△ADG的中位线
∴ EF//BC.
 8.请阅读下列材料: 8.请阅读下列材料:
问题:如图1,在菱形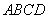 和菱形 和菱形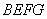 中,点 中,点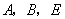 在同一条直线上, 在同一条直线上,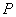 是线段 是线段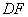 的中点,连结 的中点,连结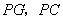 .若 .若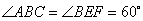 ,探究 ,探究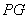 与 与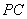 的位置关系及 的位置关系及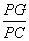 的值. 的值.
小聪同学的思路是:延长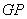 交 交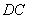 于点 于点 ,构造全等三角形,经过推理使问题得到解决. ,构造全等三角形,经过推理使问题得到解决.
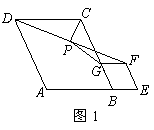 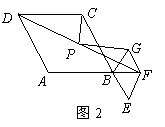
请你参考小聪同学的思路,探究并解决下列问题:
(1)写出上面问题中线段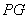 与 与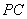 的位置关系及 的位置关系及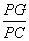 的值; 的值;
(2)将图1中的菱形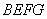 绕点 绕点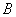 顺时针旋转,使菱形 顺时针旋转,使菱形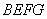 的对角线 的对角线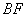 恰好与菱形 恰好与菱形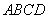 的边 的边
 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生 在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的两个结论是否发生
变化?写出你的猜想并加以证明.
解:(1)线段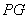 与 与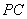 的位置关系是 的位置关系是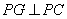 ; ;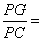 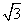 . .
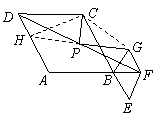 (2)猜想:(1)中的结论没有发生变化. (2)猜想:(1)中的结论没有发生变化.
证明:如图,延长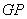 交 交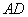 于点 于点 ,连结 ,连结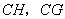 . .
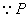 是线段 是线段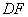 的中点, 的中点,
 . .
由题意可知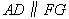 . .
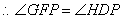 . .
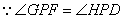 , ,
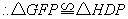 . .
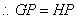 , ,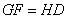 . .
 四边形 四边形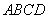 是菱形, 是菱形,
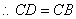 , ,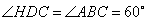 . .
由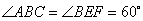 , ,
且菱形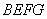 的对角线 的对角线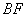 恰好与菱形 恰好与菱形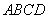 的边 的边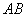 在同一条直线上, 在同一条直线上,
可得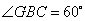 . .
 . .
 四边形 四边形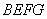 是菱形, 是菱形,
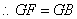 . .
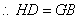 . .
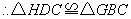 . .
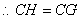 , ,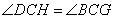 . .
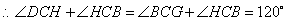 . .
即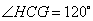 . .
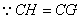 , , , ,
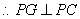 , ,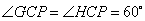 . .
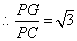 . .
|