|
练习
一、选择题
1. 将抛物线y=3x2如何平移,可得到抛物线y=3(x-2)2-1( )
A. 向左平移2个单位,再向上平移1个单位
B. 向左平移2个单位,再向下平移1个单位
C. 向右平移2个单位,再向上平移1个单位
D. 向右平移2个单位,再向下平移1个单位
2. 如图,是二次函数y=ax2+bx+c的图象,点P(a+b,ac)是坐标平面内的点,则点P在第( )象限。
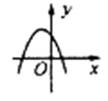
A. 一 B. 二 C. 三 D. 四
3. 下列抛物线,对称轴是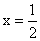 的是( ) 的是( )
A. 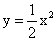 B. y=x2+2x C. y=x2+x+2 D. y=x2-x-2 B. y=x2+2x C. y=x2+x+2 D. y=x2-x-2
4. 在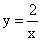 ,y=x+5,y=x2的图象中,是中心对称图形且对称中心是原点的图象共有( ) ,y=x+5,y=x2的图象中,是中心对称图形且对称中心是原点的图象共有( )
A. 0个 B. 1个 C. 2个 D. 3个
5. 抛物线y=x2-3x+2不经过第( )象限。
A. 一 B 二 C. 三 D.四
6. 已知二次函数y=ax2+bx+c的图象,如图所示,下列结论:
①a+b+c>0;②a-b+c>0;③abc<0;④2a-b=0,其中正确结论的个数是( )
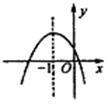
A. 1 B. 2 C. 3 D. 4
7. 抛物线y=-x2+2kx+2与x轴公共点的个数为( )
A. 0 B. 1 C. 2 D. 以上答案都不对
8. 关于二次函数y=ax2+bx+c的图象有下列命题:
(1)当c=0时,函数的图象过原点;
(2)当c>0且函数的图象开口向下时,方程ax2+bx+c=0必有两个不等实根;
(3)函数图象最高点的纵坐标是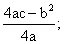
(4)当b=0时,函数的图象关于y轴对称。 其中正确命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
9.向上发射一枚炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx。若此炮弹在第7秒与
第14秒时的高度相等,则下列时间中对应高度最高的是( )
A. 第8秒 B. 第10秒 C. 第12秒 D. 第15秒
10.如图,把抛物线 与直线 与直线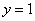 围成的图形 围成的图形 绕原点 绕原点 顺时针旋转 顺时针旋转 后,再沿 后,再沿 轴向 轴向
右平移1个单位得到图形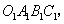 则下列结论错误的是 ( ) 则下列结论错误的是 ( )
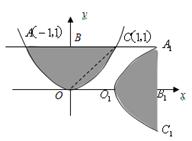
A.点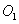 的坐标是 的坐标是 B.点 B.点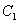 的坐标是 的坐标是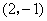
C.四边形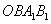 是矩形 D.若连接OC则梯形 是矩形 D.若连接OC则梯形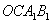 的面积是3 的面积是3
二、填空题
11.二次函数y=x2+2x-5取最小值时,自变量x的值是__________.
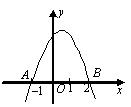
12.如图,抛物线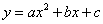 ( (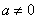 )与 )与 轴的两个交点分别为 轴的两个交点分别为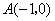 和 和 ,当y<0 ,当y<0
时,x的取值范围是____________.
13. 试写出一个开口方向向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线的解析式
为______________.
14. 已知二次函数y=kx2-7x-7的图象和x轴有公共点,则k的取值范围是________.
15.二次函数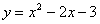 的图象关于原点O(0, 0)对称的图象的解析式是___________. 的图象关于原点O(0, 0)对称的图象的解析式是___________.
16. 抛物线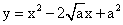 的顶点在直线y=2上,则a的值是_____________. 的顶点在直线y=2上,则a的值是_____________.
17. 已知二次函数y=x2-2x-3的图象与x轴交于点A、B两点,在抛物线上有点C,且△ABC的面积等于8,
则C点的坐标为_________________.
18. 已知抛物线y=x2-2bx+4的顶点在坐标轴上,则b的值是_______________.
三、解答题
19. 直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=ax2+bx+c与x轴的另一个交点为A,且对称轴是直线x=2。求该抛物线的函数表达式.
20.已知抛物线的顶点P(3,-2),且在x轴上所截得的线段AB的长为4。
(1)求此抛物线的解析式;
(2)抛物线上是否存在点Q,使△QAB的面积等于12,若存在,求点Q的坐标,若不存在,请说明理由。
参考答案:
1.D 2.C 3.D 4.B 5.C 6.B 7.C 8.C 9.B 10.D
11.-1;
12.x<-1或x>2;
13.y=x2-4x+3
14.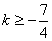 且k≠0; 且k≠0;
15.y=-x2-2x+3;
16.2;
17.(1,-4)、(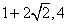 )、( )、(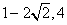 ); );
18.0,±2;
19.y=x2-4x+3
20.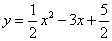 ,Q(-1,6)、(7,6) ,Q(-1,6)、(7,6)
|