综合练习
一、选择题：
　　1．下列说法中正确的是（ ）
　　A．是一个无理数　　　　 B．函数的自变量的取值范围是
　　C．4的平方根是2　　　　　　D．若点和点关于轴对称，则的值为5

　　2．下列命题是假命题的是（ ）
　　A．一组数据的方差是
　　B．要了解一批新型导弹的性能，采用抽样调查的方式
　　C．“购买一张福利彩票，中奖” ，这是一个随机事件
　　D．分别写有三个数字的三张卡片，从中任意抽取两张，则卡片上的两数之积为正数的概率
　 　　为

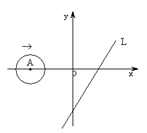
　　3．如下图，平面直角坐标系中，⊙A的圆心在x轴上，半径为１，直线为y=2x-2，若⊙A沿x轴向右运
　 　　动，当⊙A与有公共点的过程中，点A可以移动的最大距离是（ ）
　　　　　　　　　　　　　　　　　　
　　A． 　　　B．3 　　　C．　　　 D．

　　4．科技馆为某机器人编制一段程序，如果机器人在平地上按照图中所示的步骤行走，那么该机器人所
　 　　走的总路程为 （ ）
　　　　　　　　　　　　　　　　　　　
　　A．6米．　　B．8米．　　C．12米．　　D．不能确定．

　　5．如图，边长为1的菱形ABCD绕点A旋转，当B、C两点恰好落在扇形AEF的弧EF上时，弧BC的长度等
　 　　于（ ）
　　　　　　　　　　　　　　　　　　　　
　　A．　　　B．　　　 C．　　　D．

二、填空题：
　　6．有一个运算程序，可以使：⊕ = (为常数)时，得 （+1）⊕ = +1， ⊕（+1）=
　 　　-2.现在已知1⊕1 = 2，那么2008⊕2008 =_____________．

　　7．对于平面内任意一个凸四边形ABCD，现从以下四个关系式①AB=CD；②AD=BC；③AB∥CD；
　 　　④∠A=∠C 中任取两个作为条件，能够得出这个四边形ABCD是平行四边形的概率是____________

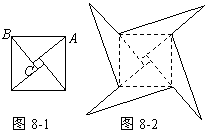
　　8．图8-1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若
　 　　，，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图8-2所示的
　 　　“数学风车”，则这个风车的外围周长是_____________．
　　　　　　　　　　　　　　　　　　

　　9．观察表一，寻找规律．表二、表三分别是从表一中选取的一部分，则a+b的值为
11 13
17 b

0 1 2 3 …
1 3 5 7 …
2 5 8 11 …
3 7 11 15 …
… … … … …
11
14
a
　　　　　　　　　　　　　　表二 　　　　　　　　　　　　　　表三
　

　　　　表一

　　10．如图，在△ABC中，AB=AC，M、N分别是AB、AC的中点，D、E为BC上的点，连结DN、EM。若AB=13cm
　　　　BC=10cm，DE=5cm，则图中阴影部分的面积为_____________cm2。
　　　　　　　　　　　　　　　　　

　　11．如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和BP为边做等边△APC和等边△BPD，
　　　　则线段CD长度的最小值是_____________
　　　　　　　　　　　　　　　　　　　　

　　12．在△ABC中，∠B=25°，AD是BC边上的高，并且，则∠BCA的度数为________

三、解答题：
　　13、计算：

　　14．先化简代数式÷，再求它的值，其中 a是9的算术平方根。

　　15．在平面直角坐标系xOy中，直线y=-x绕点O顺时针旋转90°得到直线，直线与反比例函数的图象的一个交点为A（a ,3），试确定反比例函数的解析式。

　　16．已知关于x的方程有整数根，求非负整数a及相应方程的根 。

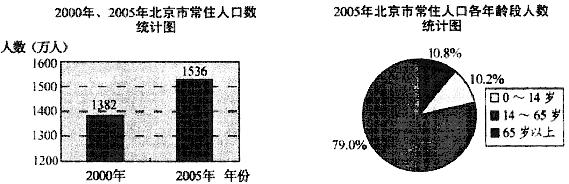
　　17．根据北京市统计局公布的2000年，2005年北京市常住人口相关数据，绘制统计图表如下：
　　　
年份 大学程度人数
（指大专及以上）		 高中程度人数（含中专） 初中程度人数 小学程度人数 其他人数
2000年 233 320 475 234 120
2005年 362 372 476 212 114
　　请利用上述统计图表提供的信息回答下列问题：
　　（1）从2000年到2005年北京市常住人口增加了多少万人？
　　（2）2005年北京市常住人口中，少儿（0至14岁）人口约为多少万人？
　　（3）请结合2000年和2005年北京市常住人口受教育程度的状况，谈谈你的看法．

　　18、如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且AB＝AD＝AO．
　　（1）求证：BD是⊙O的切线．
　　（2）若点E是劣弧BC上一点,AE与BC相交于点F，且△BEF的面积为8，cos∠BFA＝，求△ACF的面积.
　　　　　　　　　　　　　　　　　　

　　19．如图，在一个长40米，宽30米的矩形操场上，小刚从点A出发，沿着A→B→C的路线以3米/秒的速度跑向C 地，当他出发4秒后，小华有东西要交给他，就从A地出发沿小刚走的路线追赶，当小华跑到距B 地米的D处时，他和小刚在阳光下的影子恰好重叠在同一条直线上，此时A处一根电线杆在阳光下的影子也恰好在对角线AC上
　　（1） 求他们的影子重叠时，两人相距多少米？（DE的长）
　　（2） 求小华追赶小刚的速度是多少？（精确到0.1米/秒）
　　　　　　　　　　　　　　　　　

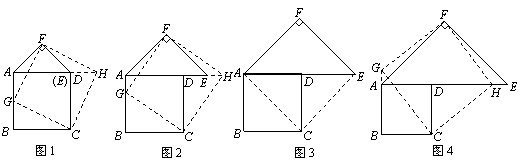
　　20．在图1至图5中，正方形ABCD的边长为a，等腰直角三角形FAE的斜边AE＝2b，且边AD和AE在同一直线上．
　　操作示例：当2b＜a时，如图1，在BA上选取点G，使BG＝b，连结FG和CG，裁掉△FAG和△CGB并分别拼接到△FEH和△CHD的位置构成四边形FGCH．
　　思考发现：小明在操作后发现：该剪拼方法就是先将△FAG绕点F逆时针旋转90°到△FEH的位置，易知EH与AD在同一直线上．连结CH，由剪拼方法可得DH=BG，故△CHD≌△CGB，从而又可将△CGB绕点C顺时针旋转90°到△CHD的位置．这样，对于剪拼得到的四边形FGCH（如图1），过点F作FM⊥AE于点M（图略），利用SAS公理可判断△HFM≌△CHD，易得FH=HC=GC=FG，∠FHC=90°．进而根据正方形的判定方法，可以判断出四边形FGCH是正方形．
　　实践探究：
　　（1）正方形FGCH的面积是_____________；（用含a，b的式子表示）
　　（2）类比图1的剪拼方法，请你就图2—图4的三种情形分别画出剪拼成一个新正方形的示意图．
　　　　　
　　联想拓展
　　小明通过探究后发现：当b≤a时，此类图形都能剪拼成正方形，且所选取的点G的位置在BA方向上随着b的增大不断上移．
　　当b＞a时，如图5的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．
　　　　　　　　　　　　　　　　　　

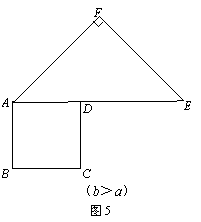
　　21．第一象限内的点A在一反比例函数的图象上，过A作AB⊥x轴于B，连接AO，已知△AOB的面积为4
　　（1）求反比例函数解析式；
　　（2）若点A的纵坐标为4，过点A的直线与x轴交于P，且△APB与△AOB相似，求所有符合条件的点P的坐
　 　　　标；
　　（3）在（2）的条件下，过点P、O、A的抛物线是否可由抛物线平移得到？若是，请说明由
　 　　　抛物线如何平移得到；若不是，请说明理由。

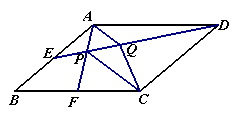
　　22．设点E是平行四边形ABCD的边AB的中点，F是BC边上一点，线段DE和AF相交于点P，点Q在线段DE上，且AQ//PC.
　　（1） 证明：PC=2AQ；
　　（2） 当点F为BC的中点时，试比较和梯形APCQ面积的大小关系，并对你的结论加以证明。
　　　　　　　　　　　　　　　　　　　

综合练习答案：
　　一、 选择题：
　　1、D 2、A 3、A 4、C 5、C

　　二、 填空题：
　　6、-2005 　　7、 　　8、76　　 9、37 　　10、30　　 11、5 　　12、65或115

　　三、解答题：
　　13、 　　　　14、，13 　　　15、

　　16、a=0时 ; a=2时

　　17、（1）154 （2）156.672 （3）受大学教育的人口明显增加，教育水平有所提高

　　18、（1）连接OB 可直接推出∠DBO=90°
　　　　（2）利用∽，面积的比为相似比的平方，可得的面积为18

　　19、（1）因为同一时刻阳光的倾斜角度相同，所以DE∥AC ，求得
　　　　（2）

　　20、（1）a2+b2；
　　　　（2）剪拼方法如图1—图3．
　　　
　　联想拓展 能；剪拼方法如图4（图中BG=DH=b）．

　　21、（1）
　　　　（2）P(4,0); P(10,0), P(-6,0)
　　　　（3）当P(4,0)或P(10,0)时,抛物线开口向下，不能由得到；
　　　　　　 当P(-6,0)时，，由向左移3个单位，向下移个单位

　　22、（1）可利用∽；或连接AC.
　　　　（2）相等