一元一次方程的复习
【学习目标】
　　一元一次方程的相关概念及解法和一元一次方程的应用。

【知识结构】
　　　　　　　

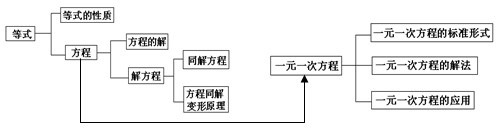
【复习要求】
　　1．了解代数式、等式、方程的区别与联系.
　　2．能说出等式的意义和等式的两条性质，并能运用等式的性质说明等式变形的依据. 注意等式性质：
　 　　两边同除以同一个不为零的数，结果仍相等。这说明两边不能同除以同一个未知数或含未知数的式
　 　　子。
　　3．进一步弄清楚方程、方程的解、解方程的意义.
　　4．会列简单的方程，会检验一个数是不是所给方程的解.
　　5．一元一次方程的标准形式：ax+b=0（其中a≠0，a，b为已知数）.
　　6．能正确运用方程同解变形的两个原理和移项法则.熟练地解一元一次方程，会灵活运用一元一次方程
　 　　解法的一般步骤. 解方程不要生搬硬套解方程的步骤，具体问题具体分析，找到最佳解法。
　　7．列方程解应用题的一般步骤是：①弄清题意，设未知数，②找出能够表示全部含义的相等关系，
　 　　③列方程，④解方程，⑤检验、写答案.
　　8．应用题是重点，需要注意：(1)设未知数时有单位时单位要写清楚；(2)列方程，方程两边所表示的
　 　　量应该相同，并且各项单位一致；(3)求得方程的解要会根据应用题的实际意义，检查所求的解是否
　 　　合理.

【思想方法总结】
　　本章主要的方法有：化归的方法，分析法，综合法和方程的思想.
　　1．化归方法，所谓化归即转化，是指求解数学问题时，将较难或较繁或未知的问题进行变换，使之化
　 　　难为易，化繁为简，化未知为已知，从而使问题得以解决的思维方法，本章中将一元一次方程逐步
　 　　变形、化简转化为ax=b(a≠0)的形式求解的过程就属于转化的方法.
　　2．分析法是从未知，看已知，逐步推向已知，即执果索因.
　　3．综合法是从已知，看未知，逐步推向未知，即由因导果.
　 　　研究数学问题时，一般总是先分析，在分析的基础上综合，列方程解应用题就是运用了分析法和综
　 　　合法相结合的数学方法.
　　4．方程的思想，方程思想设未知数（把它看成以存在的数），让代替未知数的字母和已知数一样参与
　 　　运算，列方程解应用题。本章列方程解应用题，是方程思想的具体应用.

【典型例题】
一、概念类
　　1、在下列式子(1)2x+3；(2)1-x=x-2；(3)2x-y=6；(4)x+=2中一元一次方程为______个．
　　分析：一元一次方程应满足：①等式；②一元：一个未知数；③一次：未知数的次数是1； ④整式：方程中的未知数不能出现在分母中。(1)不是等式，(2)满足，(3)含有两个未知数；(4)未知数出现在分母中。
　　答案：1

　　2、已知关于x的方程 ax + 5 = -2 - 3a与方程2x +3= -17的解相同, 则a = _________.
　　分析：首先方程2x +3= -17的解为x=-10，方程 ax + 5 =-2 - 3a与方程2x +3= -17同解，所以方程 ax + 5 = -2 - 3a的解为x=-10，那么-10a+5=-2-3a成立，这是关于a的一元一次方程，进而可求得a。
　　答案：1

二、解法类
　　3、下列方程的变形是否正确？如果不正确，指出错在何处，并写出正确的变形.
　　（1）由3+x=-6, 得x=-6+3.
　　　　 答：不正确.错在数3从方程的等号左边移到右边时没有变号，正确的变形是
　　　　 　　由 3+x=-6，得 x=-6-3.
　　（2）由9x=-4, 得 .
　　　　 答：不正确，错在被除数与除数颠倒（或分子与分母颠倒了）.正确的变形是
　　　　 　　由9x=-4, 得 .
　　（3）由5=x-3, 得x=-3-5.
　　　　 答：不正确.错在移项或等号两边的项对调时把符号弄错，正确的变形是
　　　　 　　由5=x-3，得5+3=x, 即x=5+3.
　　（4）由，得3x-2=5-4x+1.
　　　　 答：不正确，没有注意到分数中的“分数线”也起着括号的作用，因此当方程两边的各项
　　　　 　　都乘以5时，+1没有变号.正确的变形是
　　　　 　　由，得3x-2=5-(4x+1)，进而得3x-2=5-4x-1.
　　（5）由，得2(x+2)-3(5x-7)=1.
　　　　 答：不正确.错在当方程两边同乘以12时，等号右边的1漏乘12.
　　　　 　　正确的变形是由，得2(x+2)-3(5x-7)=12.

　　4、解方程
　　分析：可将每一项里分母、分子中的小数化为整数，然后再约分，或分子、分母直接约分.
　　解：
　　　　各项分别化简得，(8x-3)-(25x-4)=12-10x
　　　　8x-3-25x+4=12-10x,
　　　　-17x+1=12-10x,
　　　　-17x+10x=12-1,
　　　　-7x=11,
　　　　.
　　　　∴ 原方程的解为.

　　5、若关于x的方程(k-4)x=6有正整数解，求自然数k的值.
　　解：(k-4)x=6,
　　　　,
　　　　∵为正整数，且k为自然数，
　　　　∴k-4为6的正约数，即k-4的值分别为1，2，3，6.
　　　　当k-4=1时，k=5;
　　　　当k-4=2时，k=6;
　　　　当k-4=3时，k=7;
　　　　当k-4=6时，k=10.
　　　　答：自然数k的值分别为5，6，7，10.

　　6、解关于x的方程：
　　(1) (m-1)x=(m-1)(m-2)
　　解：(m-1)x=(m-1)(m-2)
　　　　当m-1≠0，即m≠1时，
　　　　方程的解为x=m-2.
　　　　当m-1=0，即m=1时，原方程变为0·x=0.这时原方程的解为任意数.
　　(2) (m-1)(m-2)x=m-1.
　　解：(m-1)(m-2)x=m-1
　　　　当(m-1)(m-2)≠0，即m≠1且m≠2时，方程的解为.
　　　　当m-1=0，即m=1时，原方程变为0·x=0.这时原方程的解为任意数。
　　　　当m-2=0，即m=2时，原方程变为0·x=1，这时原方程无解.

三、应用类
　　需要掌握以下几类题型：商品销售、银行存贷款、积分、行程、工程、数字问题、日历、比例分配、方案选择。希望同学们能根据下面的例子掌握此类型题目的解题思路。
1.商品销售
　　此类问题主要涉及的关键量：进价，标价，实际售价，利润，利润率。熟记这些量间的基本关系式：
　　 商品的利润=商品的实际售价-商品的进价.（这里不考虑其它因素）
　　 商品的利润率=
　　 商品打折后的售价=商品的标价÷10×折扣数.
　　另外在解决商品的利润率的问题中，还涉及如下关系式.
　　
　　注意会由基本关系式推出式子的变形，以便于解决问题.
　　例如：由×100%=利润率，可得商品的实际售价=商品的进价×(1+利润率).

　　7、商店里的皮上衣每件标价为2200元，在一次促销活动中，它打八折销售，结果仍获利10%，求此商品的进价.
　　分析：题中的相等关系是
　　　　　商品的进价×(1+利润率)=商品的实际售价.
　　解：设此商品的进价为x元，依题意 (1+10%)x=2200×0.8.
　　　　解这个方程，得x=1600.
　　答：此商品的进价为1600元.

　　8、以现价销售一件商品的利润率为30%，如果商家在现有的价格基础上先提价40%，后降价50%的方法进行销售，商家还能有利润吗？为什么？
　　解：设该商品的成本为a元，则商品的现价为(1+30%)a元，依题意其后来折扣后的售价为
　　　　(1+30%)a×(1+40%)(1-50%)=0.91a.
　　　　∵0.91a-a=-0.09a, ∴ ×100%=-9%.
　　答：商家不仅没有利润，而且亏损的利润率为9%.

2.银行存贷款
　　9、夏老师欲购买一辆汽车，销售商告诉夏老师，若采取分期付款方式：一种付款方式是第一月付4万元，以后每月付款一万元；另一种付款方式是前一半时间每月付款1万四千元，后一半时间，每月付款1万1千元；两种付款方式中付款钱数和付款时间都相同。销售商还说若夏老师一次性付款，可少付车款1万6千元。夏老师看了看自己的存折决定一次性付清购车款，同学们帮夏老师算算，夏老师要付款多少万元？
　　分析：在应用题中通常利用一个（或多个）已知条件找关系式，剩下的一个条件列方程。由分期付款两种付款方式中付款时间都相同设时间是未知数，进而由付款钱数相同列方程。
　　解：设分期付款总共付x期，由题意得：
　　　　
　　　　解得：x=12
　　　　故4+(x-1)=4+(12-1)=15(万元)
　　　　15-1.6=13.4（万元）
　　答：夏老师要付款13.4万元。

3.积分
　　10、足球比赛的计分规则为：胜一场积3分，平一场得一分，负一场积0分，一支足球队在某个赛季共需比赛14场，现已比赛8场，输了一场，得17分。
　　（1）前8场比赛中，这支球队共胜了几场？
　　（2）这支球队打满14场比赛，最高能得多少分？
　　分析：总得分=胜场得分+平场得分+负场得分。第2问要得最高分，前8场的比赛得分已确定，只要后面（14-8）场比赛每次都赢。
　　解：（1）设这支球队共胜了x场球，则平了(8-x-1)场球，由题意得：
　　　　　　 3x+(8-x-1)=17
　　　　　　 解得：x=5
　　　　（2）17+（14-8）×3=17+18=35
　　　　　　 答：前8场比赛中，这支球队共胜了5场。这支球队打满14场比赛，最高能得35分。

4.行程问题
　　行程问题是与实际生活联系密切的一类问题，也是变化最多的一类问题。对于行程问题，抓住相向、背向、同向、追上、相遇等关键词语，借助草图的直观性，对题目进行具体分析，找到等量关系列方程，有利于培养分析问题、解决问题的能力。
　　11、A、B两地相距216千米，甲、乙分别在A、B两地，若甲骑车的速度为15千米/时，乙骑车的速度为12千米/时。
　　（1）甲、乙同时出发，相向而行，几小时后相遇？相遇地点离B地有多远？
　　　　 解：设x小时后甲、乙相遇，
　　　　　　　
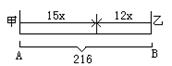
　　　　 　　依题意，得15x+12x=216。
　　　　 　　解这个方程，得x=8。
　　　　 　　当x=8时，12x=12×8=96。
　　　　 答：8小时后甲、乙相遇，相遇地点离B地96千米。
　　（2）甲、乙同时出发，同向而行，乙在前、甲在后，问甲几小时追上乙？
　　　　 解：设x小时后甲追上乙。
　　　　　　　
　　　　 　　依题意，得15x-12x=216。
　　　　 　　解这个方程，得x=72。
　　　　 答：需72小时甲追上乙。
　　（3）甲、乙同时出发，背向而行，问几小时后他们相距351千米？
　　　　 解：设x小时后，甲、乙相距351千米，
　　　　　　　
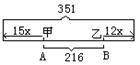
　　　　 　　依题意，得15x+12x=351-216，
　　　　 　　解这个方程，得x=5。
　　　　 答：5小时后，甲、乙相距351千米。
　　（4）甲、乙相向而行，甲出发三小时后乙才出发，问乙出发几小时后两人相遇？
　　　　 解：设乙出发x小时后两人相遇。
　　　　　　　　
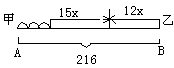
　　　　 　　依题意，得15(3+x)+12x=216,
　　　　 　　解这个方程，得x=.
　　　　 答：乙出发小时后，甲、乙两人相遇。
　　（5）甲、乙相向而行，要使他们相遇于AB的中点，乙要比甲先出发几小时？
　　　　 解：设当乙比甲早出发x小时，使甲、乙二人相遇于AB的中点。
　　　　　　　　　　
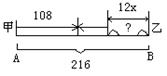
　　　　 　　依题意，得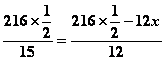，解这个方程，得x=.
　　　　 答：只要乙比甲先出发小时，两人就能相遇于AB的中点。
　　（6）甲、乙同时出发，相向而行，甲到达B处，乙到达A处都分别立即返回，几小时后相遇？
　　　　 相遇地点距离A有多远？
　　　　 解：设x小时后甲乙相遇，
　　　　　　
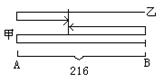
　　　　 　　依题意，得15x+12x=216×3
　　　　 　　解这个方程，得x=24.
　　　　 　　当x=24时，12x-216=72.
　　　　 答：24小时后两人相遇，相遇地点距离A地72千米。

　　12、一架飞机往返于甲、乙两城市之间，顺风飞行需3小时，逆风飞行需3小时20分；若风速是每小时30千米，求甲、乙两城之间的距离。
　　解法1：设甲、乙两城之间相距x千米，
　　　　　　依题意，得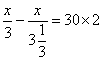，解这个方程，得x=1800。
　　答：甲、乙两城相距1800千米。
　　解法2：设飞机的速度为x千米/时，则飞机顺风飞行时，速度为(x+30)千米/时，
　　　　　　飞机逆风飞行时速度为(x-30)千米/时。
　　　　　　依题意：3(x+30)= (x-30)
　　　　　　解这个方程，得x=570，当x=570时，3(x+30)=3×600=1800。
　　答：甲、乙两城相距1800千米。

5.工程问题
　　13、一项工程，甲队独做20天完成，乙队独做30天完成.甲队单独做了5天，剩下的部分由甲、乙合做，几天可以完成？
　　分析：甲队单独做20天完成任务，一天完成总工作量的；乙队单独做30天完成，一天完成总工作量的；两队合做一天完成总工作量的.这个问题中的相等关系是：甲独做的工作量+甲、乙合做的工作量=全部工作量.
　　解：设剩下的部分由甲、乙合做x天可以完成，根据题意，
　　　　得,解这个方程，得x=9.
　　答：剩下的部分由甲、乙合做，9天可以完成.
　　说明：工程问题中，工作总量=工作效率×工作时间，常常将工作总量看作“1”.

6．数字问题
　　14、有一个三位数的个位数字为1，如果把这个1移到最前面的位置上，那么所得的新三位数的2倍比原数多15，求原来的三位数.
　　分析：此题属于数字问题，其中三位数如何用代数式表示是列方程的关键，一般来说，一个三位数，百位上的数为a，十位上的数为b，个位上的数为c，则这个三位数写成100a+10b+c.在题目中，如果把原三位数的前两位数字看成整体并设为x，则原三位数可表示为： 10x+1.同样新三位数表示为100×1+x.
　　解：设原三位数的前两位数为x，则原三位数是10x+1，新三位数为100×1+x，依题意得.
　　　　2(100×1+x)-15=10x+1
　　　　解这个方程得 x=23.
　　　　∴ 原三位数是10x+1=10×23+1=231.
　　答：原三位数为231.

7.日历
　　15、在下边的日历中, 带阴影的方框里有四个数, 随着方框的移动，请你探究这四个数的关系. 设最小的一个数为a, 则这四个数之和为 _________ (用含a的代数式表示).
　　　　　　　　　　　　　　　
　　分析：在日历中最小的数为a，则和它相邻的右边
　　　　　这个数为a+1。又一周为7天，则a下面的数为
　　　　　a+7，和它相邻的数为a+8。
　　答：4a+16

8.比例分配
　　16、某车间有28名工人生产甲、乙两种零件，每人每天平均可生产甲种零件12个或乙种零件18个，要是按1：2配套组装。问：生产两种零件的工人应如何安排？
　　分析：利用甲、乙两种零件配套生产的总组数相同列方程。
　　解：设生产甲零件的工人数为x人，则生产乙零件的工人数为（28-x）人，由题意得:
　　　　
　　　　解得：x=12
　　　　28-12=16
　　答：生产甲种零件的工人有12人，生产乙种零件的工人有16人。

9.方案选择
　　17、某牛奶加工厂有鲜奶9吨，若在市场上直接销售鲜奶，每吨可获取利润500元，制成酸奶销售，每吨可获取利润1200元；制成奶片销售，每吨可获利润2000元，该工厂的生产能力是：如制成酸奶，每天可加工3吨；制成奶片每天可加工1吨，受人员限制，两种加工方式不可同时进行，受气温条件限制，这批牛奶必须在4天内全部销售或加工完毕.为此，该厂某领导提出了两种可行方案：
　　方案1：尽可能多的制成奶片，其余直接销售鲜牛奶；
　　方案2：将一部分制成奶片，其余制成酸奶销售，并恰好4天完成，你认为选择哪种方案获利最多，
　　 　　　为什么？
　　解：(1)若选择方案1，依题意，
　　　　　 总利润=2000元×4+500元×(9-4)=10500元.
　　　　(2)若选择方案2.
　　 　　　设将x吨鲜奶制成奶片，则用(9-x)吨鲜奶制成酸奶销售，依题意，得
　　　　　 ，
　　　　　 解这个方程，得x=1.5.
　　　　　 当x=1.5时，9-x=7.5.
　　　　　 总利润=2000元×1.5+1200元×7.5=12000元.
　　　　　 ∵ 12000＞10500,
　　　　　 ∴ 选择方案2较好.
　　答：选择方案2获利最多，只要在四天内用7.5吨鲜奶加工成酸奶，用1.5吨的鲜奶加工成奶片.