教学目标:
1、结合具体情境,理解邻补角、对顶角的概念,探索并掌握对顶角相等;理解垂线、垂线段等概念,掌握 “过一点有且仅有一条直线垂直于已知直线”的基本事实,会用三角尺或量角器过一点画一条直线的垂线,了解垂线段最短的性质,了解点到直线距离的意义并会度量点到直线的距离.
2、能初步应用本节学过的知识解释生活中的现象及解决简单的实际问题,体会研究几何图形的意义;在观察、操作、想象、推理、交流的过程中,发展空间观念,初步形成积极参与数学活动、与他人合作交流的意识,激发学习图形与几何的兴趣.
教学重点:
垂线的定义、性质、判定和画法
教学内容解析:
1、邻补角、对顶角的概念和性质
观察演示剪刀剪布的过程→抽象出相交直线→画相交直线→找小于平角的角的个数→两两配对→分类→分类标准→总结形成概念→猜想数量关系→度量数量关系验证猜想→由一般性推出性质定理→用演绎推理的形式对发现结论进行证明→用性质定理说明剪刀剪布的原理→应用:知一求三.
2、垂线的概念
观察木条转动→抽象出两条直线交角的变化→抽离出特殊数量关系→定义特殊的位置关系:垂直→垂直的有关概念及符号语言表述→应用:90°角
3、垂线的性质
画一条直线的垂线(多种方法:三角尺、量角器、折纸)→过直线上一点和直线外一点作已知直线的垂线→发现垂线的存在性和唯一性→总结出垂线的性质定理.
4、垂线段的性质
实际问题→抽象成数学模型→画图、测量→归纳出结论(垂线段最短)→实际应用.
5、垂线的画法
按步骤操作:一压线、二找点、三画线、四标垂足.
例题解析:
1.如图所示,∠1和∠2是对顶角的图形有( )

A.1个 B.2个 C.3个 D.4个
分析:考察对顶角的概念,选A
2.如图1所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
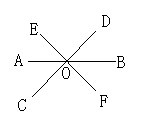
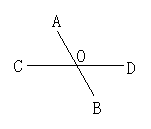
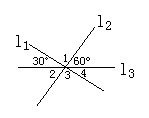
图 1 图2 图3
分析:考察对顶角性质、邻补角概念的应用,选B
3.下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;
③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
分析:①、③正确选B
4.如图2所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A.62° B.118° C.72° D.59°
分析:由对顶角相等可求出∠AOD,再由邻补角互补求∠AOC,选A
5.如图3所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是( )
A.∠1=90°,∠2=30°,∠3=∠4=60°; B.∠1=∠3=90°,∠2=∠4=30
C.∠1=∠3=90°,∠2=∠4=60°; D.∠1=∠3=90°,∠2=60°,∠4=30°
分析:选D
6.如图4所示,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB; B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段; D.线段BD是点B到AD的垂线段
分析:考察垂线段的概念,线段AD是点A到BC的垂线段,选C
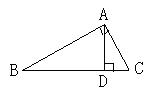
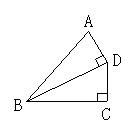
图 4 图5
7.如图4所示,能表示点到直线(线段)的距离的线段有( )
A.2条 B.3条 C.4条 D.5条
分析:AB、AD、AC、BD、CD选D
8.下列说法正确的有( )
①在平面内,过直线上一点有且只有一条直线垂直于已知直线;
②在平面内,过直线外一点有且只有一条直线垂直于已知直线;
③在平面内,过一点可以任意画一条直线垂直于已知直线;
④在平面内,有且只有一条直线垂直于已知直线.
A.1个 B.2个 C.3个 D.4个
分析:①、②正确,选B
9.如图5所示,AD⊥BD,BC⊥CD,AB=acm,BC=bcm,则BD的范围是( )
A.大于acm B.小于bcm
C.大于acm或小于bcm D.大于bcm且小于acm
分析:根据垂线段最短,选D
10.到直线L的距离等于2cm的点有( )
A.0个 B.1个; C.无数个 D.无法确定
分析:选C
11.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm B.2cm; C.小于2cm D.不大于2cm
分析:选D
12.如图所示,O为直线AB上一点,∠AOC=
(1)求∠COD的度数;(2)判断OD与AB的位置关系,并说明理由.
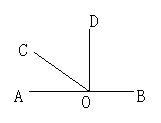
分析:由∠AOC和∠BOC互补,可求出∠AOC等于45°,再根据OC是∠AOD的平分线,求出∠COD等于45°;根据∠AOD等于90°得出OD与AB互相垂直。
13.若4条不同的直线相交于一点,则图中共有几对对顶角?若n条不同的直线相交于一点呢?
解:2条直线交于一点有2对对顶角;3条直线交于一点有3组两条相交直线,共6对对顶角;n条直线交于一点有(n-1+n-2+…+2+1)组两条相交直线,共n(n-1)对对顶角。
14.在一个平面内任意画出6条直线,最多可以把平面分成几个部分?n条直线呢?
解:1条直线把平面分成2部分;2条直线把平面分成4部分;3条直线把平面分成7部分;6条直线把平面分成1+1+2+3+4+5+6=22部分;n条直线把平面分成1+1+2+…+n=1+
15.(2001.南通)如图16所示,直线AB,CD相交于O,若∠1=40°,则∠2的度数为________
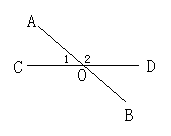
解:根据邻补角的概念,可得∠2等于140°。
16.(2001.杭州)如图7所示,一辆汽车在直线形的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄,设汽车行驶到P点位置时,离村庄M最近,行驶到Q点位置时,离村庄N最近,请你在AB上分别画出P,Q两点的位置.
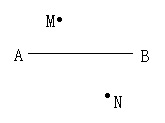
解:根据垂线度最短,分别过M、N两点向AB做垂线,垂足分别为Q、P。
