角的概念、性质和应用
【知识结构】
　　　　　　　　　　　　　

【教学目标】
　　1．理解角，互余、互补角的概念，掌握它们的性质。
　　2．掌握度，分，秒的换算，会计算角的和，差，倍，分。
　　3．理解角的和差，角平分线的概念。
　　4．培养学生逻辑推理能力及归纳、总结、类比的能力。
　　5．培养学生“文—图—式—符”相互转化的能力，使学生领略到逻辑推理的严密性。

【本周重点、难点】
　　1．重点：角的相关概念和图形的画法训练．
　　2．难点：有关角的综合理解与应用．
【知识要点】
1． 角的概念：
　　（1）有公共端点的两点射线组成的图形叫做角，这个公共端点叫做角的顶点，这两条射线叫做角的边.
　　（2）角还可以这样定义：把一条射线OA，绕着它的端点O，从原来的位置OA旋转到另一个位置OB，这时
　 　　　OA和OB就生成了一个角，记作∠AOB，其中OA、OB分别叫做角的始边和终边，点O叫做角的顶点．

2．角的分类：
　　（1）平角：射线OA绕O点旋转，当始边OA与终边OB互为反向延长线时，称∠AOB为平角．
　　（2）直角：平角的一半叫做直角；
　　（3）锐角：大于零度且小于直角的角叫做锐角；
　　（4）钝角：大于直角且小于平角的角叫做钝角

3．角的度量：
　　目前角的度量采用角度制，即把一个周角分成360等份，每一份叫做1度的角，记作1°，并且，．
　　在这种度量下，1周角=360°，1平角=180°，1直角=90°．

4．角的平分线：
　　把一个角分成两个相等的角的射线叫做角的平分线．

【典型例题】
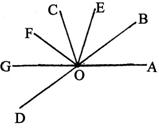
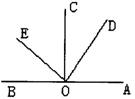　　1．已知：如图，O是直线AB上一点，∠AOC=90°，∠DOE=90°，求：
　　（1）图中共有多少个角?
　　（2）图中共有多少对互余的角?
　　（3）图中共有多少对互补的角?
　　说明：根据题目要求，能用分类讨论的思想方法，不重不漏地把对象的个数算准确，是应该掌握的有关“计数”问题的基本能力．
　　解：（1）若分别以OA、OD、OC、OE为角的始边，依次数得角的个数4+3+2+1=10（个）．
　　　　（2）∵ ∠AOC=∠COB=∠DOE=90°，
　　　　　　 ∴ ∠AOD与∠DOC，∠DOC与∠COE，∠COE与∠EOB互余．
　　　　　　 ∵ ∠DOC=∠EOB，
　　　　　　 ∴ ∠AOD与∠EOB互余．
　　　　　　 综上所述，图中共有四对互余的角．
　　　　（3）∵ ∠AOC=∠COB=∠DOE=90°．
　　　　　　 ∴ ∠AOC、∠COB、∠DOE这三个角中，每两个角互补，
　　　　　　 又∵ ∠DOC=∠EOB，
　　　　　　 ∴ ∠DOC、∠EOB分别与∠AOE互补，
　　　　　　 同理，∠AOD、∠COE分别与∠DOB互补．
　　　　　　 综上所述，图中共有七对互补的角．

　　2．中午12点到13点之间，何时时钟的时针与分针的夹角是88°．
　　分析：分针一分钟旋转，时针一分钟旋转．分针从12点到13点的转动过程中有两次与时针的夹角是88°。
　　解：设从12点开始，经过分钟时针与分针的夹角是88°，
　　　　则，或，
　　　　解得，或。
　　答：当12点16分或12点分时，时针与分针的夹角是88°。

　　3．已知：如图，∠AOE=88°，∠BOD=31°，求图中所有锐角的度数之和．
　　　　　　　　　　　　　　　　　　　　　
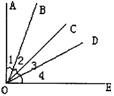
　　分析：为了表示简洁方便，设∠AOB=∠1，∠BOC=∠2，∠COD=∠3，∠DOE=∠4，用这些角表示出所有锐角，然后进行求和，整理过程尽量往∠AOE与∠BOD上“凑”。
　　解：设∠AOB=∠1，∠BOC=∠2，∠COD=∠3，∠DOE=∠4，则:
　　　　∠AOC=∠1+∠2， ∠BOD=∠2+∠3，∠COE=∠3+∠4，
　　　　∠AOD=∠1+∠2+∠3，∠BOE=∠2+∠3+∠4，∠AOE=∠1+∠2+∠3+∠4．
　　　　∵ 图中十个锐角之和=4∠1+6∠2+6∠3+4∠4
　　　　　　　　　　　　　 =4(∠1+∠2+∠3+∠4)+2(∠2+∠3)
　　　　　　　　　　　　　 =4∠AOE+2∠BOD
　　　　　　　　　　　　　 =4×88°+2×31°
　　　　　　　　　　　　　 =414°
　　　　∴ 图中所有锐角的度数之和为414°．

　　4．已知：如图，∠AOC=∠BOD=150°，若∠AOD=3∠BOC, 求：∠BOC．
　　　　　　　　　　　　　　　　　　　　　
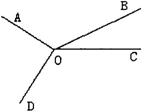
　　分析：利用方程的思想解几何题。
　　解：设∠BOC=x，由已知可得：150°+3x+(150°- x)=360°，
　　　　解得x=30°，
　　　　∴ ∠BOC=30°．

　　5．一个角的余角比它的补角的还少40°，求这个角的大小．
　　分析：由已知给的相等关系，可构造关于这个角的一个方程。
　　解：设这个角为，则它的余角为，它的补角为。由已知得：
　　　　。
　　　　解得：
　　　　即角的大小为。

　　6．已知，如图，点E、C、F在同一直线上，AC平分∠FCD，BC平分∠DCE，求∠ACB。
　　　　　　　　　　　　　　　　　　
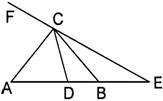
　　分析：整体表示成部分的和：∠ACB可以表示成∠DCA与∠DCB的和，利用角平分线的性质，∠ACB表示为∠ECF的一半。
　　解：∵ E、C、F在同一直线上，
　　　　∴ ∠ECF=∠FCD+∠DCE=180°．（平角的定义）
　　　　∵ AC平分∠FCD，BC平分∠DCE（已知），
　　　　∴ ∠DCB=∠DCE，∠DCA=∠DCF。（角平分线的性质）
　　　　∴ ∠ACB=∠DCA+∠DCB=∠DCE+∠FCD=(∠DCE+∠FCD)=90°。
　　　　∴ ∠ACB=90°。

　　7．已知：如图，∠AOB：∠BOC：∠COD：∠DOA=1：2：3：4，OE平分∠BOC，OF、OG三等分∠COD。
　　　　　　求：∠COD，∠EOG的度数．
　　　　　　　　　　　　　　　　　　
　　分析：一般给出比例式的形式时，通常设“一份”为x，利用方程进行求解。
　　解：∵ ∠AOB：∠BOC：∠COD：∠DOA=1：2：3：4，
　　　　∴ 设∠AOB=，∠BOC=，∠COD=，∠DOA=
　　　　∵ ∠AOB+∠BOC+∠COD+∠DOA=360°
　　　　∴
　　　　∴
　　　　∴ ∠COD=，
　　　　又∵OE平分∠BOC，
　　　　∴∠EOC=∠BOC=
　　　　∴ ∠EOG=∠EOC +∠GOC=
　　　　即∠COD=∠EOG=108°

　　8．∠AOB的顶点O为端点引射线OC，使∠AOC：∠BOC=3：2，若∠AOB=30°，求∠AOC的度数．
　　分析：∠AOB的顶点O为端点引射线OC使∠AOC：∠BOC=3：2，满足此条件的射线OC有两种可能：
　　⑴∠AOB的内部；⑵∠AOB的外部。注意此类几何题要先画图。
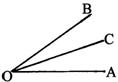　　解：①当射线OC在∠AOB内部时，
　　　　　∵ ∠AOC：∠BOC=3：2，
　　　　　∠AOB=∠AOC+∠BOC，
　　　　　∠AOB=30°，
　　　　　∴ ∠AOC=∠AOB=
　　　　②当射线OC在∠AOB外部时，
　　　　　∵ ∠AOC：∠BOC=3：2，
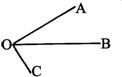
　　　　　∠AOB=∠AOC-∠BOC=∠AOC∠AOC=∠AOC，
　　　　　即有：∠AOC=3∠AOB
　　　　　又∵ ∠AOB=30°
　　　　　∴ ∠AOC=3∠AOB=90°
　　　　　综上所述，∠AOC=18°或90°

　　9．如图，∠AOC与∠AOB的和为180°，OM、ON分别是∠AOC与∠AOB的平分线，且∠MON=40°，试求∠AOC与∠AOB的度数。
　　　　　　　　　　　　　　　
　　证明：（法一）
　　　　　　∵ OM、ON分别平分∠AOC、∠AOB，
　　　　　　∴ ∠AOM∠AOC，∠AON∠AOB
　　　　　　∴ ∠MON=∠AOM∠AON=(∠AOC∠AOB)
　　　　　　∵ ∠MON=40°
　　　　　　∴ ∠AOC∠AOB=80°
　　　　　　又∵ ∠AOC+∠AOB=180°
　　　　　　∴ ∠AOC=130°，∠AOB=50°
　　（法二）设∠MOB=x°，
　　　　　　∵ ∠MON=40°，
　　　　　　∴ ∠NOB=∠MON∠MOB=(40x)°
　　　　　　∵ ON是∠AOB的角平分线
　　　　　　∴ ∠AOB=2∠NOB=2(40x)°=(802x)°
　　　　　　∵ OM是∠AOC角平分线
　　　　　　∴ ∠AOC=2∠AOM=2(∠MOB+∠AOB)=2(x+802x)°=(1602x)°
　　　　　　∵ ∠AOC+∠AOB=180°
　　　　　　∴ (1602x)°+(802x)°=180°
　　　　　　∴ x=15
　　　　　　∴ ∠AOC=，∠AOB=