一．例题讲解：
1．解方程
解：
，
，
，
，
2．若关于x的方程
有正整数解，求自然数k的值．解：
，
，∵
为正整数，且k为自然数，∴
为6的正约数，即k-4的值分别为l，2，3，6．当k-4=1时，k1=5；
当k-4=2时，k2=6；
当k-4=3时，k3=7；
当k-4=6时，k4=10．
答：自然数k的值分别为5，6，7，10．
3．解关于x的方程：
解：
当
，即
时，方程的解为
．当
，即m=1时，原方程变为0·x=0．这时原方程的解为任意有理数．4．有一个三位数的个位数字为1，如果把这个1移到最前面的位置上，那么所得的新三位数的2倍比原数多15，求原来的三位数．分析：此题属于数字问题，其中三位数如何用代数式表示是列方程的关键，一般来说，一个三位数，百位上的数为a，十位上的数为b，个位上的数为c，则这个三位数写成100a+10b+c．在题目中，如果把原三位数的前两位数字看成整体并设为x，则原三位数可表示为：10x+1．同样新三位数表示为100×1+x．
解：设原三位数的前两位数为x，则原三位数是10x+1，新三位数为100×1+x，
依题意得．2(100×1+x)-15=10x+1
解这个方程得x=23．
∴ 原三位数是10x+1=10×23+1=231．
答：原三位数为231．
6．某牛奶加工厂有鲜奶9吨，若在市场上直接销售鲜奶，每吨可获取利润500元，制成酸奶销售，每吨可获取利润1200元；制成奶片销售，每吨可获利润2000元，该工厂的生产能力是：如制成酸奶，每天可加工3吨；制成奶片每天可加工1吨，受人员限制，两种加工方式不可同时进行，受气温条件限制，这批牛奶必须在4天内全部销售或加工完毕．为此，该厂某领导提出了两种可行方案：方案1：尽可能多的制成奶片，其余直接销售鲜牛奶；
方案2：将一部分制成奶片，其余制成酸奶销售，并恰好4天完成，
你认为选择哪种方案获利最多，为什么?
解：（1）若选择方案1，依题意，
总利润=2000元×4+500元×(9-4)=10500元．
（2）若选择方案2．
设将x吨鲜奶制成奶片，则用(9-x)吨鲜奶制成酸奶销售，
依题意，得
，解这个方程，得
．当时，
．总利润=2000元×1.5+1200元×7.5=12000元．
∵ 12000>10500，
∴ 选择方案2较好．
答：选择方案2获利最多，只要在四天内用7.5吨鲜奶加工成酸奶，用1.5吨的鲜奶加工成奶片．
7．工程问题（工作时间×工作效率=工作量）甲、乙两人要各自在车间加工一批数量相同的零件，甲每小时可加工25个，乙每小时可加工20个．甲由于先去参加了一个会议，比乙少工作了1小时，结果两人同时完成任务，求每人加工的总零件数量．
【分析】相等关系：甲工作的时间=乙工作的时间
．解法一：设每人加工的总零件数量为x个，
由题意得，
，解得，x=100．答：每人加工的总零件数量为100个．
【分析】相等关系：甲加工的总零件数量=乙加工的总零件个数．
解法二：设甲的工作时间为x小时，则乙的工作时间为
小时．由题意得，
，解得，
．
个答：每人加工的总零件数量为100个．
8．收割一块水稻田，若每小时收割4亩，预计若干小时完成，收割
后，改用新式农机，工作效率提高到原来的
倍，因此比预计时间提早1小时完成，求这块水稻田的面积．【分析】相等关系：预计所用时间=实际所有时间+1．
解：设这块水稻田的面积为x亩．
由题意得，
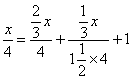，解得，
。答：这块水稻田的面积为36亩．
9．有一个蓄水池，装有甲、乙两个进水管和一个排水管，单独开甲管12h可把空池注满，单独开乙管16h可将空池注满，单独开排水管15h可把满池的水放完，现甲、乙两管同时开6h后关闭乙管，同时打开排水管，问再过几小时可把水放满?【分析】相等关系：甲、乙开6h的工作量+甲、排水管的工作量=1．
解：设再过x小时可把水放满．
由题意得，
，解得，
。答：再过7.5小时可把水放满．
10．甲、乙两辆汽车分别从A、B两站同时开出，相向而行，途中相遇后继续沿原路线行驶，再分别到达对方车站后立即返回，两车第二次相遇时距A站34km，已知甲车速度是70km／h，乙车速度是52km／h，求A、B两站间的距离．【分析】相等关系：甲车行驶的时间=乙车行驶的时间
解：设A、B两站间的距离为xkm．
由题意得，
，解得，
．答：A、B两站间的距离为122km．
11．某手表每小时比准确时间慢3min，若在清晨4点30分，与准确时间对准，则当天上午该手表指示时间为10点50分时，准确时间应该是________．【分析】相等关系：准确时间一慢的时间=10点50分．
解：设准确时间为x，
由题意得，
，解得，
．
点=11点10分．答：准确时间应该是11点10分．
12．国家规定个人发表文章，出版图书获得的稿费的纳税计算办法是：（1）稿费不高于800元的不纳税；（2）稿费高于800元又不高于4000元的应缴纳超过800元的那一部分稿费的14%的税；（3）稿费高于4000元的应缴纳全部稿费的11%的税，今知丁老师获得一笔稿费，并缴纳个人所得税420元，问丁老师的这笔稿费有多少元?解：∵ 4000元×11%=440元 > 420元，
∴ 丁老师的稿费低于4000元．
设丁老师的稿费是x元，依题意，
．解这个方程，得x=3800．
答：丁老师的这笔稿费是3800元．
13．某市居民生活用电基本价格为每度0.4元．若每月用电量超过a度，超过部分按基本电价的70%收取．（1）某户五月份用电84度，共交电费30.72元，求a是多少；
（2）若六月份的电费平均为每度0.36元，求六月份共用多少度电，应交纳多少电费?
解：（1）根据题意，得
．解这个方程，得a=60．
（2）设六月份共用电x度，据题意得
，解这个方程，得x=90，0.36x=32.4．
答：六月份共用90度，应交电费32.4元．
14．甲乙两车间共120人，其中甲车间人数比乙车间人数的4倍少5人．（1）求甲、乙两车间各有多少人?
（2）若从甲、乙两车间分别抽调工人，组成丙车间研制新产品，并使甲、乙、丙三个车间的人数比为
13：4：7，那么甲、乙两车间要分别抽调多少工人?
分析：（1）此题有两个未知数，它们之间存在一定的关系，通常设一个未知数为x，把另一个未知数用x的代数式表示出来，再根据相等关系列方程．
相等关系有：甲车间人数+乙车间人数=120人，
甲车间人数=4×乙车间人数-5人．
（2）可设一份为x，则甲、乙、丙三个车间人数分别为13x，4x，7x．再根据甲车间人数+乙车间人数+丙车间人数=120，这一相等关系列方程．
解：（1）设乙车间有x人，那么甲车间有
人，根据题意，得
，解这个方程，得x=25．
．（2）设甲、乙、丙三个车间人数比的一份为x人，
则这三个车间的人数依次为13x人、4x人、7x人．依题意
13x+4x+7x=120．
解得：x=5．
当x=5时，95-13x=95-13×5=30，
25-4x=25-4×5=5．
答：原甲、乙车间各有95人和25人．需分别从甲、乙两车间分别抽调30人和5人组成丙车间．
15．（1）某个商品的进价是500元，把它提价40%后作为标价．如果商家要想保住12%的利润率搞促销活动，请你计算一下广告上可写出打几折?分析：以进价500为基础，分别考虑折扣销售的实际价格如何用代数式表示．
解：设该商品打x折，依题意，则
。
．答：该商品的广告上可写上打八折．
（2）某件商品的标价是按获得25％的利润率计算出来的，后因库房积压和急需回收资金，决定降价出售．如果每件商品仍要获得10％的利润率．试问可按现行标价的几折出售?
分析：（1）与（2）的区别在于没有给出该商品的进价．从（1）的解题过程中我们可以看出进价的500元只是在列式子时起作用，对未知数的值没有影响．因此，解（2）时，为了便于列出方程等号两边的代数式，不妨设该商品的进价为a元（a >0）．
解：设该商品的进价为a元（a >0），按标价的x折出售．依题意，则
．答：该商品可按标价的八点八折出售。
二．巩固练习：
1．对方程
的下列变形中，正确的是（ ）A．
B．
C．
D．
2．甲能在11天内独立完成某项工作，乙的工作效率比甲高10%，那么乙独立完成这项工作的天数
为（ ）
A．10天 B．12.1天 C．9.9天 D．9天
3．一个长方形的周长为26cm，这个长方形的长减少1cm，宽增加2cm，就可成为一个正方形，设长方形
的长为x cm，设长方形的长为x cm，则可列方程（ ）
A．
B．
C．
D．
4．一件工作甲独做要a天完成，乙独做要b天完成，如果两人合作3天完成此工作的（ ）
A．
B．
C．
D．
5．某个体商贩在一次买卖中同时卖出两件上衣，每件售价均为135元，若按成本计算，其中一件盈利
25%，一件亏本25%， 则在这次买卖中他（ ）
A．不赚不赔 B．赚9元 C．赔18元 D．赚18元
6．单项式
的系数是________， 次数是________．7．
与是同类项， 则n=________．8．若
，则
________．9．已知2a与2-a互为相反数， 则a=________
10．已知关于x的方程ax+5=2-3a与方程x=-10的解相同，则a=________．
11．有一个两位数，个位数字与十位数字的和是9，如果将个位数字与十位数字对调后所得新数比原数
大9，则原来的两位数是________________．
12．先化简，再求值：
，其中
，，
13．
．14．
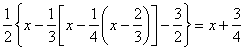．15．
．16．已知
是关于x的一元一次方程，求m的值．17．如果方程
与关于x的方程
的解相同，求
的值．18．A，B两地的路程为360千米，甲车从A地出发开往B地，每小时行驶72千米，甲车出发25分钟后，乙车从B地出发开往A地，每小时行驶48千米，两车相遇后，各车仍按原速度原方向继续行驶，直到两车相距100千米停止．问：甲车从出发开始到现在共行驶了多少小时?
19．某车间加工A型和B型两种零件，平均一个工人每小时能加工7个A型零件或3个B型零件．而且3个A型与2个B型配套，就可以包装进库房，剩余不能配套的只能暂时存放起来．如果B型零件单独存放，对环境的要求远高于A型零件．已知该车间原有工人69名．
（1）怎样分配工人工作才能保证生产出的产品及时包装运进库房?
（2）后来因为工作调动，有4名工人调离了该车间．那么你认为现在应该怎样分配工人工作最合适呢?
请通过计算说明你的依据．
20．夏季为了节约用电，常对空调采取调高设定温度和清洗设备两种措施。某宾馆先把甲、乙两种空调的设定温度都调高1摄氏度，结果甲种空调比乙种空调每天多节电27度；再对乙种空调清洗设备，使得乙种空调每天的总节电量是只将温度调高1摄氏度后节电量的1.1倍，而甲种空调的节电量不变，这样两种空调每天共节电405度。求只将温度调高1摄氏度后两种空调每天各节电多少度?
21．国外营养学家做了一项研究，甲组同学每天正常进餐，乙组同学每天除正常进餐外，每人还增加600毫升牛奶。一年后发现，乙组同学平均身高的增长值比甲组同学平均身高的增长值多2.01cm，甲组同学平均身高的增长值比乙组同学平均身高的增长值的
少0.34cm。求甲、乙两组同学平均身高的增长值．22．某停车场的收费标准如下：中型汽车的停车费为6元／辆，小型汽车的停车费为4元／辆。现在停车场有50辆中、小型汽车，这些车共缴纳停车费230元，问中、小型汽车各多少辆?
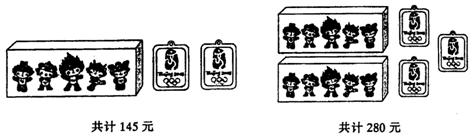
23．某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品，根据下图提供的信息，求一盒“福娃”玩具和一枚徽章的价格各是多少元?
24．某区中学生足球赛共赛8轮（即每队均参赛8场），胜一场得3分，平一场得1分，输一场得0分，在这次足球联赛中，猛虎足球队踢平的场数是所负场数的2倍，共得17分，试问该队胜了几场．
参考答案：
1．D 2．A 3．B 4．C 5．C
6．
7．4 8．-1 9．-2 10．
l1．45 12．713．
14．
15．
16．
17．
18．419.（1）分配27人生产A型零件，分配42人生产B型零件。
（2）分配26人生产A型零件，分配39人生产B型零件。
20．只将温度调高1℃后，甲种空调每天节电207度，乙种空调每天节电180度。
21．甲、乙两组同学平均身高增长值为4.67cm和6.68cm
22．中型汽车15辆，小型汽车35辆
23．一盒“福娃”玩具和一枚徽章的价格分别为125元和10元
24．该队踢胜5场
