|
寒假专题一(有理数)
综合练习:
一. 判断:
( ) ①一个数与它的相反数的商为-1
( ) ②任何一个有理数的平方都是非负数.
( ) ③若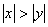 ,则x>y. ,则x>y.
( ) ④任何一个有理数都有相反数和倒数.
( ) ⑤ 两数之和为正数, 则这两个数一定都是正数
( ) ⑥有奇数个负因数的乘积为负数.
( ) ⑦-a表示负数.
( ) ⑧相反数等于它本身的数是0
( ) ⑨绝对值大于它本身的数是负数, 绝对值等于它本身的数是0
( ) ⑩若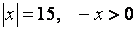 ,则x=-15. ,则x=-15.
二.选择题:
1.数a的倒数是( )
A.-a B. C. C.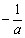 D. D. 或不存在 或不存在
2.已知四种说法:①a>0时,|a|=a; a<0时,|a|=-a;②|a|就是a与-a中较大的数;③|a|就是数轴
上a到原点的距离;④对于任意有理数,-|a|≤a≤|a|.其中说法正确的个数是( )
A.1 B.2 C.3 D.4
3. 有四个说法:①有最小的有理数;②有绝对值最小的有理数;③有最小的正有理数;④没有最大的
负有理数。上述说法正确的是( )
A.①② B.③④ C.②④ D.①②
4. 若|x-1|+|y+3|+|z-5|=0,则(x+1)(y-3)(z+5)的值是( )
A.120 B.-15 C.0 D.-120
5. 下列各对算式中,结果相等的是( )
A.-a6与(-a)6 B.-a3与|-a|3
C.[(-a)2]3与(-a3)2 D.(ab)3与ab3
6. 下列说法正确的是 ( )
A.近似数3.5和3.50精确度相同 B.近似数0.0120有3个有效数字
C.近似数7.05×104精确到百分位 D.近似数3千和3000的有效数字都是3
7. 下面结论中正确的是 ( )
A.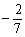 比 比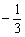 大 B. 大 B.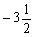 的倒数是 的倒数是 C.最小的负整数是 -1 D.0.5 > C.最小的负整数是 -1 D.0.5 > 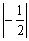
8. 下列计算正确的是 ( )
A. B. B.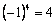 C. C. D. D.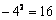
9. 有理数在数轴上的对应点位置如图所示:则( )

A.a+b>0 B.a+b<0 C.a-b=0 D.a-b>0
10. 若ab<0且a+b>0,那么( ) .
A.a>0 ,b>0 B.a<0,b<0
C.a、b异号且负数的绝对值较大 D.a、b异号且正数的绝对值较大
11. 计算 所得结果为( ). 所得结果为( ).
A.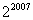 B. B.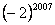 C. C.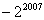 D.-2 D.-2
12. 出租汽车在东西方向路上行驶,约定向东为正,向西为负。当天行驶记录如下(单位:千米):
+16,-8,+4,-11,+17,-6,+7,-12.若出租车行驶每千米耗油量a升,则该天共耗油( )
A.7a升 B.81a升 C.23a升 D.57a升
13. 如图是一个三阶幻方,由9个数组成,并且每横行,竖行和对角线上的和都相等,则中间的数
为( )。
A.8 B.5 C.6 D.7
14.一根1m长的绳子, 第一次剪去一半, 第二次剪去剩下的一半, 如此剪下去, 第六次以后剩下的绳
子的长度为 ( )
A. m B. m B.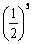 m C. m C. m D. m D.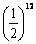 m m
 15.已知数 15.已知数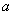 、 、 、 、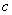 在数轴上的位置如图所示,化简 在数轴上的位置如图所示,化简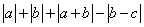 的结果是( ). 的结果是( ).
A.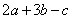 B. B.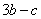
C.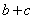 D. D.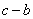
三.填空题
1.有理数- 的相反数是____________,绝对值是____________. 的相反数是____________,绝对值是____________.
2.从数轴上观察大于-4且小于3的整数有____________.
3.比较大小:-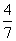 - -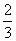 , -(-7)____________-│-7│. , -(-7)____________-│-7│.
4.若(a+1)2+|b-3|=0,则a=________,b=________,a+b=________,a-b=________.
5.用四舍五入法,求1.549的近似数(保留两个有效数字)是____________,7531000用科学记数法表
示的结果是____________.
6.甲地海拔高度-40m,乙地的海拔高度-10m,____________地比____________地高出____________m.
7.已知:a=3,则|-a|-|a+4|=____________.
8.甲、乙两数和为-23.6,乙数为-8.9,则乙数比甲数大____________.
9.不大于3.9的最大整数是____________,不大于-3.9的最大整数是____________.
10.当x=____________时,式子(x+2)2+5有最小值,最小值是____________.
11.已知|m| = 5, |n| = 2, |m-n| = n-m, 则m + n =___________.
12.观察下列各式,
-6×7=-42;
-66×67=-4422;
-666×667=-444222;
(-666×667=-2×3×111×667=-222×2001)
-6666×6667=-44442222.
则第六个式子的结果为____________,第 n个式子的结果为____________.
四、计算题
1.(-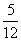 )÷ )÷ ×(-1.5)÷(- ×(-1.5)÷(-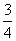 ) 2. ) 2.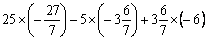
3.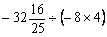 4. 4.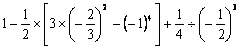
5.(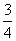 - -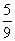 - - )÷ )÷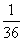 6.-(-32)-32÷23-(-4)2×5 6.-(-32)-32÷23-(-4)2×5
五、化简求值
已知有理数a,b,c在数轴上对应的点的位置如图所示:
化简:|3a-c|+|2a+b|-|c-b|
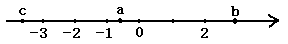
六、应用题
小王上周五在股市以收盘价(收市时的价格)每股25元买进某公司股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况(周六,周日不交易,单位:元).
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌(元) |
+2 |
-0.5 |
+1.5 |
-1.8 |
+0.8 | 根据上表回答问题
(1) 星期三收盘时,该股票每股多少元?
(2) 本周内该股票收盘时的最高价,最低价分别是多少?
(3) 已知买入股票与卖出股票均需支付成交金额的5‰的交易费。若小王在本周五以收盘价将全部股票
卖出去,它的收益情况如何?
参考答案:
一. 判断:
×,提示:注意0的相反数还是0,0不能作除数;
√,
×,如, ,但-5<3; ,但-5<3;
×,提示:0没有倒数;
×,如 -1+3=2,2>0,但-1<0;
×,提示:若其它因数有一个为0,则它们的乘积为0;
×,用字母表示数,a可以表示正数、负数或零;
√,提示:-a=a,则2a=0.故a=0;
×,提示:要求绝对值大于它本身,即|a|>a。当a≥0时,|a|=a;当a>0时,|a|>0>a,满足条件。
绝对值等于本身,即|a|=a。当a≥0时,|a|=a;当a<0时,|a|>0>a.故绝对值等于本身的
数为非负数。
√,提示:|x|=15,则x=15或x=-15。又-x>0,则x<0,故x=-15.
二. 选择题:
1、D,2、C,3、C,4、D,5、C,6、B,7、A,8、A,9、B,10、D
11、A;12、B;13、D;14、C;15、B
三.填空题
1. , , ; 2.-3,-2,-1,0,1,2; 3.﹥, ﹥; 4.-1,3,2,-4; ; 2.-3,-2,-1,0,1,2; 3.﹥, ﹥; 4.-1,3,2,-4;
5.1.5, 7.531×106; 6.乙,甲,30; 7.-4;
8.5.8; 9.3,-4; 10.-2,5; 11.-3或-7;
12.-666666×666667=-444444222222;
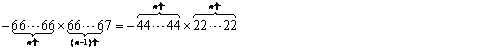
四、计算题
1、- ;2、 ;2、 ;3、 ;3、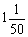 ; 4、 ; 4、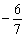 ;5、-14;6、-75 ;5、-14;6、-75
五、化简求值
5a
提示:由图所示,可得c<-3<-1<a<0<2<b.∴3a-c>0, 2a+b>0, c-b<0,
∵ |3a-c|+|2a+b|-|c-b|=(3a-c)+ (2a+b) -[-(c-b)]=3a-c+(2a+b)+(c-b)=3a-c+2a+b+c-b=5a.
∴原式=5a.
六、应用题
解:(1) 25+2-0.5+1.5=28(元)
所以星期三收盘时,该股票每股28元。
(2) 该股票每日收盘价格相比周五买入价25元的涨跌情况
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌(元) |
+2 |
+1.5 |
+3 |
+1.2 |
+2 | +1.2<+1.5<+2<+3,故本周内周四收盘价最低,周三收盘价最高;
即周三收盘时价格最高,此时每股为28元,周四收盘时价格最低,此时每股为26.2元;
(3) 小王买入价为(25×1000)元,此时交易费为(25×1000×5‰)元,
小王卖出价为(27×1000)元,此时交易费为(27×1000×5‰)元,故小王的收益为:
27×100-27×1000×5‰-25×1000×5‰-25×1000=1740(元)
所以共赚1740元
|