本章教学目标：
1．了解与三角形有关的线段（边、高、中线、角平分线）；理解三角形两边之和大于第三边，会根据
三条线段的长度判断它们能否构成三角形；会画出任意三角形的高、中线、角平分线；了解三角形
的稳定性．
2．了解与三角形有关的角（内角、外角），会用平行线的性质与平角的定义证明三角形内角和等于
180°，探索并了解三角形的一个外角等于与它不相邻的两个内角的和．
3．了解多边形的有关概念（边、内角、外角、对角线、正多边形），探索并了解多边形的内角和与外
角和公式．
4．通过探索平面图形的镶嵌，知道任意一个三角形、四边形或正六边形可以镶嵌平面，并能运用这几
种图形进行简单的镶嵌设计．
本章知识结构框图：
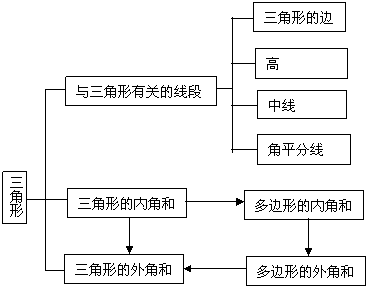
本章练习题：
练习一 与三角形有关的边
一、 选择题：
1. 已知三角形的两边长分别为2cm和7cm，第三边的长为ccm，则c的取值范围是（ ）．
A． 2＜c＜7 B． 7＜c＜9 C． 5＜c＜7 D ． 5＜c＜9
2. 在△ABC中，若AB＝AC，其周长为12，则AB的取值范围是（ ）．
A．AB＞6 B．AB＜3 C．4＜AB＜7 D．3＜AB＜6
3. 现有长度分别为2cm，3cm，4cm，5cm的木棒，从中任取三根，能组成三角形的个数为（ ）．
A．1 B．2 C．3 D．4
4. 如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，那么这个三角形是（ ）．
A．锐角三角形 B．钝角三角形
C．直角三角形 D．不能确定
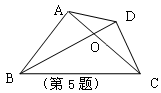
5. 如图，图中共有不同的三角形的个数是（ ）．
A．4 B．6 C．8 D．10
二、 填空题：
6.
△ABC中，AB＝AC，且BC＝8，BD是AC边长上的中线，分△ABC的周长为两部分，已知它们的差为2，则AB边的长为_____________．
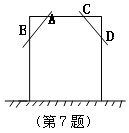
7. 工人师傅在做完门框后，为防止变形常常像右图中所示的那样上两条斜拉的木
条（即图中的AB、CD两根木条），这样做根据的数学道理是___________．
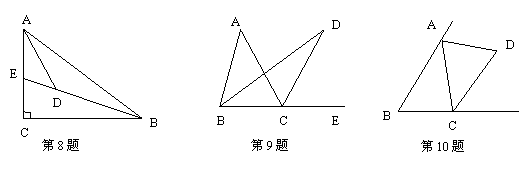
8. 已知，△ABC中，D、E分别为BC边上顺次两点，且BD=DE=EC，连结AD、AE，则
图中面积相等的三角形有____________对．
三、 解答题：
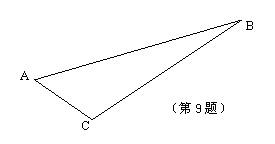
9. 已知，钝角△ABC，分别画出AC边上的高BD，BC边上的中线AE及△ABC的角平分线CF．
10. 在平面直角坐标系下描出下列各点，并求△ABC的面积：
（1）已知，A（－4，－5）、B（－2，0）、C（4，0）；
（2）已知，A（－5，4）、B（－2，－2）、C（0，2）．
11. 已知，AD、AE分别是△ABC的高和中线，AB＝6cm，BC＝10 cm，AC＝8 cm，∠CAB＝90º．求：
（1）AD的长；
（2）△ABE的面积；
（3）△ACE和△ABE周长的差．
12. 已知，如图，D为△ABC内任意一点，求证：AB+AC
BD+CD．
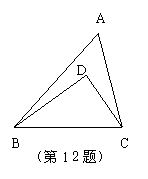
练习二 三角形的内角
一、选择题:
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形 B.钝角三角形; C.直角三角形 D.钝角或直角三角形
2.下列说法正确的是( )
A.三角形的内角中最多有一个锐角; B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角; D.三角形的内角都大于60°
3.已知三角形的一个内角是另一个内角的
,是第三个内角的
,则这个三角形各内角的度数分别为( )A.60°,90°,75° B.48°,72°,60°
C.48°,32°,38° D.40°,50°,90°
4.已知△ABC中,∠A=2(∠B+∠C),则∠A的度数为( )
A.100° B.120° C.140° D.160°
5.已知三角形两个内角的差等于第三个内角,则它是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.等边三角形
6.设α,β,γ是某三角形的三个内角,则α+β,β+γ,α+γ 中 ( )
A.有两个锐角、一个钝角 B.有两个钝角、一个锐角
C.至少有两个钝角 D.三个都可能是锐角
7.在△ABC中,∠A=
∠B=
∠C,则此三角形是( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
二、填空题:
8.三角形中,若最大内角等于最小内角的2倍,最大内角又比另一个内角大20°,则此三角形的最小内角的
度数是________.
9.在△ABC中,若∠A+∠B=∠C,则此三角形为_______三角形;若∠A+∠B<∠C,则此三角形是_____三角形.
10.已知等腰三角形的两个内角的度数之比为1: 2, 则这个等腰三角形的顶角为_______.
11.在△ABC中,∠B,∠C的平分线交于点O,若∠BOC=132°,则∠A=_______度.
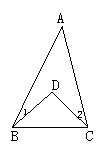
12.如图所示,已知∠1=20°,∠2=25,∠A=35°,则∠BDC的度数为________.
三、解答题:
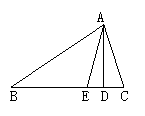
13.如图所示,在△ABC中,AD⊥BC于D,AE平分∠BAC(∠C>∠B),试说明∠EAD=
(∠C-∠B).
14.在△ABC中,已知∠B-∠A=5°,∠C-∠B=20°,求三角形各内角的度数.
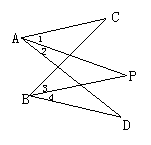
15.如图所示,已知∠1=∠2,∠3=∠4,∠C=32°,∠D=28°,求∠P的度数.
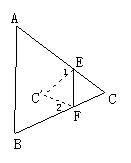
16.如图所示,将△ABC沿EF折叠,使点C落到点C′处,试探求∠1,∠2与∠C的关系.
练习三 三角形的外角
一、选择题:
1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法确定
2.如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数
为( )
A.30° B.60° C.90° D.120°
3.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90° B.110° C.100° D.120°
4.已知等腰三角形的一个外角是120°,则它是( )
A.等腰直角三角形; B.一般的等腰三角形; C.等边三角形; D.等腰钝角三角形
5.如图1所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°
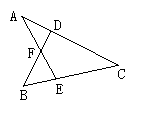
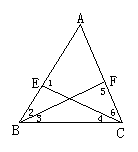
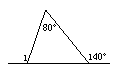
图1 图2 图3
6.如图2所示,在△ABC中,E,F分别在AB,AC上,则下列各式不能成立的是( )
A.∠BOC=∠2+∠6+∠A; B.∠2=∠5-∠A; C.∠5=∠1+∠4; D.∠1=∠ABC+∠4
二、填空题:
7.三角形的三个外角中,最多有_______个锐角.
8.如图3所示,∠1=_______.
9.如果一个三角形的内角和与一个外角的和是225°,则与这个外角相邻的内角是____度.
10.已知等腰三角形的一个外角为150°,则它的底角为_____.
11.如图4所示,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,
∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°, 则∠BOC=_______,∠D=_____,∠E=_______.
12.如图5所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.
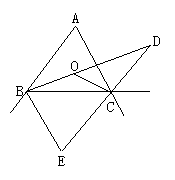
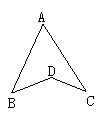
图4 图5
三、解答题:
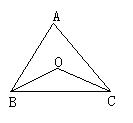
13.如图所示,在△ABC中,∠A=70°,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.
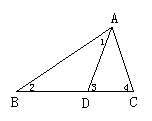
14.如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°, 求∠DAC的度数.
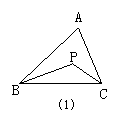
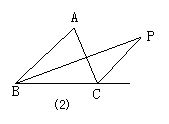
15.如图所示,在△ABC中,∠A=α,△ABC的内角平分线或外角平分线交于点P, 且∠P=β,试探求下列各图中α与β的关系,并加以说明.
练习四 多边形及其内角和
一、填空题：
1. 过五边形的一个顶点，可以作_________条对角线，把这个五边形分成_____________个三角形，则
五边形的内角和为_____________．
2. n（n≥3）边形的内角和为_____________，外角和为_____________．
3. 四边形的内角和为________，六边形的内角和为________，七边形的内角和为________，九边形的
内角和为_____________．
4. 一个多边形的内角和等于它的外角和的三倍，则这个多边形是_____________边形．
5. 一个多边形的内角和与它的外角和的总和为1080°，则它的边数是_____________．
6. 一个多边形的各内角都等于144°，则这个多边形是_____________边形.
7. 一个多边形的内角和为2340°，若每个内角都相等，则每个外角的度数是____．
8. 在四边形ABCD中，∠A=120°，∠D=90°，∠C=∠D，那么∠B=___．
9. 一个正多边形的内角和比一个五边形的内角和多540°，则这个多边形的每个外角的度数是_____．
10. 一个多边形，除去一个内角外，其余各角之和是3290°,则这个内角的度数是_____________．
二、选择题：
11. 若一个多边形从一个顶点，只能引出四条对角线，那么这个多边形是（ ）边形．
A．六 B．七 C．八 D．九
12. 六边形有（ ）条对角线．
A．7 B．8 C．9 D．10
13. 如果一个多边形的内角和等于它的外角和的两倍，则这个多边形是（ ）边形．
A．四 B．五 C．六 D．七
14. 如果一个多边形的边数增加1，那么它的内角和增加（ ）．
A．0° B．90° C．180° D．360°
三、解答题：
15. 四边形ABCD中，如果∠A+∠C=180°，∠A：∠B：∠C=2：3：7，
求∠A、∠B、∠C、∠D的度数．
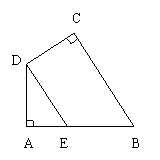
16. 已知，如图，四边形ABCD中，∠A=∠C=90°，E是AB上一点，且∠ADC=∠DEB，求证：（1）DE//BC；（2）∠EDC=90°．
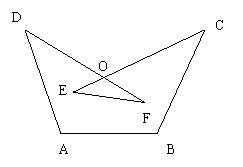
17. 如图，求∠A+∠B+∠C+∠D+∠E+∠F．
18.一个多边形的每一个内角都相等,一个内角与一个外角的度数之比为m:n,其中m,n是互质的正整数,求这个多边形的边数(用m,n表示)及n的值.
练习五 镶嵌
一、选择题:
1.用形状、大小完全相同的图形不能镶嵌成平面图案的是( )
A.等腰三角形 B.正方形 C.正五边形 D.正六边形
2.下列图形中,能镶嵌成平面图案的是( )
A.正六边形 B.正七边形 C.正八边形 D.正九边形
3.不能镶嵌成平面图案的正多边形组合为( )
A.正八边形和正方形 B.正五边形和正十边形
C.正六边形和正三角形 D.正六边形和正八边形
4.如图所示,各边相等的五边形ABCDE中,若∠ABC=2∠DBE,则∠ABC等于( )
A.60° B.120° C.90° D.45°
5.用正三角形和正十二边形镶嵌,可能情况有( )
A.1种 B.2种 C.3种 C.4种
6.用正三角形和正六边形镶嵌,若每一个顶点周围有m个正三角形、n 个正六边形,则m,n满足的关系式
是( )
A.2m+3n=12 B.m+n=8 C.2m+n=6 D.m+2n=6
二、填空题:
7.用正三角形和正六边形镶嵌,在每个顶点处有_______个正三角形和_____ 个正六边形,或在每个顶点
处有______个正三角形和________个正六边形.
8.用正多边形镶嵌,设在一个顶点周围有m个正方形、n个正八边形,则m=_____,n=______.
9.用一种正五边形或正八边形的瓷砖_______铺满地面.(填“能”或“不能”)
三、解答题:
10.计算用一种正多边形拼成平整、无隙的图案,你能设计出几种方案?画出草图.
11.用一个正方形、一个正五边形、一个正二十边形能否镶嵌成平面图案? 说明理由.
12．请你设计在每一个顶点处由四个正多边形拼成的平面图案, 你能设计出多少种不同的方案?
13．如图所示的地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出一种用多边形(不一定是正多边形)的材料铺地面的方案?把你想到的方案画成草图
14.用黑、白两种颜色的正六边形地砖按如图3所示的规律,拼成若干个图案.
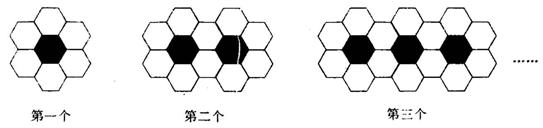
(1)第四个图案中有白色地砖_______块;
(2)第n个图案中有白色地砖________块.
练习六 三角形综合练习
一、选择题
1. 下列说法中正确的是（ ）．
A．三角形的外角大于任何一个内角
B．三角形的内角和小于外角和
C．三角形的外角和小于四边形的外角和
D．三角形的一个外角等于两个内角的和
2. △ABC中,若AB=2，BC=3，周长为偶数，则AC的长为（ ）．
A．1 B．2 C．3 D．4
3. 若一个多边形的内角和是外角和的2倍，则此多边形的边数是（ ）．
A．3 B．4 C．5 D．6
4. 三角形中最大的内角不能小于（ ）．
A．30° B．45° C．60° D．90°
二、填空题
5. 若一个三角形的三个内角的比为3：4：5，则这个三角形是_____________三角形．
6. 若等腰三角形的两边长为3和8，则它的周长是_____________．
7. 若等腰三角形的一个外角等于100°，则顶角等于_____________．
8. 如图，△ABC中，∠C=90°，∠CAB、∠CBA的平分线相交于D点，BD的延长线交AC于E，则∠ADE=___.
9. 如图，△ABC中，∠ABC的平分线与外角∠ACE的平分线交于点D，若∠D=20°，则∠A=________．
10.如图，△ABC中的两个外角平分线交于D点，若∠B=50°，则∠D=_____________．
三、解答题
11. 如图，D是△ABC的BC边上一点，∠B=∠BAD，∠ADC = 80°，∠BAC = 70°，求（1）∠B的度数；（2）∠C的度数．
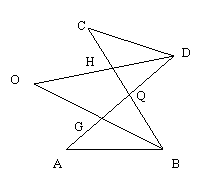
12. 如图，线段AD，BC交于Q，OD平分∠CDA且交BC于H，OB平分∠ABC且交AD于G，求(∠A+∠C)：∠O．
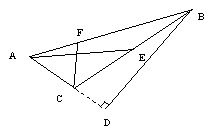
12. 如图，BE是∠ABD的平分线，CF是∠ACD的平分线，BE与CF交于点G，若∠BDC=140°，∠BGC=110°，求∠A．
14．（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A＝30°，则∠ABC＋∠ACB＝____________度，∠XBC＋∠XCB＝_____________度；
（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C，那么∠ABX＋∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX＋∠ACX的大小．
参考答案：
练习一
一、1、D 2、D 3、C 4、C 5、C
二、6、6或10 7、三角形的稳定性 8、4
三、9、如右图 10、 （1）15；（2）12
11、（1）4.8 cm，提示：面积法
（2）12
（3）2cm 12、提示：延长BD，与AC交于点E，则有AB+AE﹥BE=BD+DE，DE+CE﹥CD，所以AB+AE+DE+CE﹥BD+DE+CD，即AB+AC﹥BD+CD
练习二
一、1.A 2.C 3.B 4.B 5.C 6.C 7.B
二、8.40° 9.直角 钝角 10.36°或90° 11.84 12.80°
三、13.解：∵AD⊥BC,
∴∠BDA=90°,
∴∠BAD=90°-∠B,
又∵AE 平分∠BAC,
∴∠BAE=
∠BAC=(180°-∠B-∠C),∴∠EAD=∠BAD-∠BAE
=90°-∠B-
(180°-∠B-∠C)=90°-∠B-90°+
∠B+∠C=
∠C-∠B=
(∠C-∠B).14.∠A=50°,∠B=55°,∠C=75.
15.∠P=30°
16.解：∵∠1=180°-2∠CEF,∠2=180°-2∠CFE,
∴∠1+∠2=360°-2(∠CEF+ ∠CFE)
=360°-2(180°-∠C)
=360°-360°+2∠C=2∠C.
练习三
一、1.C 2.C 3.C 4.C 5.B 6.C
二、7.1 8.120° 9. 135° 10.30°或75° 11.120° 30° 60° 12.120°
三、13.∠BOC=125° 14.∠DAC=24°
15.
(说明略)练习四
一、1、2，3，540° 2、（n-2）·180°，360° 3、360°，720°，900°，1260° 4、八 5、6
6、十 7、24° 8、60° 9、45° 10、130°
二、11、B 12、C 13、C 14、C
三、15、∠A=40°、∠B=60°、∠C=140°、∠D=120°
16、提示：∠DEB=90°+∠ADE，∠ADC=∠EDC+∠ADE，
所以∠EDC=90°，所以DE//BC
17、360° 提示：连结CD.18、边数为
,n=1或2.（提示：充分利用边数是正整数，m,n是互质的正整数的条件）
练习五
一、1.C 2.A 3.C 4.A（提示：过B作AE的平行线，可证出四边形ACDE是菱形，从而得三角形ABC是等边三角形） 5.A 6.D
二、7.2 2 4 1 8.1 2 9.不能
三、10．略 11.略 12.略
13.(1)每个顶点周围有6个正三角形的内角,恰好组成一个周角.
(2)不能,因为正十边形的内角不能组成360°.
(3)能(图略)
14.(1)18 (2)4n+2.
练习六
一、1、B 2、C 3、D 4、C
二、5、锐角 6、19 7、80°或20° 8、45° 9、40° 10、65°
三、11、（1）40°；（2）70° 12、2 13、80°14、(1) 150°, 90°(2)不变，60°
