|
平面直角坐标系
学习目标：
1．通过实例认识有序数对，感受它在确定点的位置中的作用；
2．认识平面直角坐标系，了解点与坐标的对应关系；在给定的直角坐标系中，能根据坐标（坐标为整
数）描出点的位置，能由点的位置写出点的坐标（坐标为整数）；
3．能建立适当的平面直角坐标系描述物体的位置，体会平面直角坐标系在解决实际问题中的作用；
4．在同一平面直角坐标系中，能用坐标表示平移变换。通过研究平移与坐标的关系，看到平面直角坐
标系是数与形之间的桥梁，感受代数问题与几何问题的相互转换；
5．结合实例，了解可以用不同的方式确定物体的位置。
重点：
在给定的直角坐标系中，能根据坐标（坐标为整数）描出点的位置，能由点的位置写出点的坐标（坐标为整数）, 能用坐标表示平移变换。
内容解析：
1、平面直角坐标系：
在平面内画两条互相垂直，原点重合的数轴，组成平面直角坐标系。水平的数轴称为x轴或横轴，习惯上取向右为正方向；竖直的数轴称为y轴或纵轴，取向上为正方向，两坐标轴的交点为平面直角坐标系的原点。
2、象限的概念
建立了平面直角坐标系以后，坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分，分别叫做第一象限，第二象限，第三象限，第四象限，注意：坐标轴上的点不属于任何象限。
建立了平面直角坐标系的平面是坐标平面，坐标平面是由两条坐标轴和四个象限构成的，也就是说坐标平面内的点可以划分为六个区域：x轴，y轴，第一象限，第二象限，第三象限，第四象限，在这六个区域中，除了x轴与y轴有一个公共点（原点）外，其余区域之间均没有公共点。
3、点的坐标的概念
有了平面直角坐标系，平面内的每一个点就都可以分别用一个有序数对来表示。
若点A是平面直角坐标系中的一点，由点A向x轴作垂直线，垂足M在x轴上的坐标为a、由点A向y 轴作垂线，垂足N在y轴上的坐标为b，我们说点A的横坐标为a，纵坐标为b，合起来点A的坐标记为（a，b）。
平面内的点坐标是一个有序数对，当 a ≠ b 时，（a，b）和（b，a）分别是两个不同点的坐标，其顺序都是横坐标在前，纵坐标在后，中间用“，”分开，横、纵坐标的位置决不能颠倒（例如坐标（-2，1）和（1，-2）分别表示二象限和四象限内的点）。
反过来，若（a，b）是一个有序数对，以这个有序数对作为坐标，可以确定坐标平面内的一点A。这样，有了平面直角坐标系，我们就将几何中最基本的元素“点”与代数中最基本元素“有序数对”建立起一一对应的关系。
4、点的坐标特征
（1）x轴将坐标平面分为两部分，x轴上方的点的纵坐标为正数，x轴下方的点的纵坐标为负数，y轴把
坐标平面分为两部分，y轴左侧的点的横坐标为负数，y轴右测点的横坐标为正数。
（2）规定坐标原点的坐标为（0，0）。
（3）x轴上的点可记为（x，0），y轴上的点可记为（0，y）。
（4）坐标平面内的点p(x,y)的坐标有如下特征；
点P在第一象限 x＞0，且y＞0；
点P在第二象限 x＜0，且y＞0；
点P在第三象限 x＜0，且y＜;0；
点P在第四象限 x＞0，且y＜0；
（5）与y轴垂直的直线上的点的纵坐标相同。
（6）与x轴垂直的直线上的点的横坐标相同。
（7）一、三象限的角平分线上的点的横坐标等于纵坐标。
（8）二，四象限的角平分线上的点的横坐标与纵坐标互为相反数。
5、利用直角坐标系绘制区域内一些地点分布情况平面图
（1）建立坐标系，选择一个适当的参照点为原点，确定x轴，y轴的正方向；
（2）根据具体问题确定适当的比例尺，在坐标轴上标出单位长度；
（3）在坐标平面内画出这些点，写出各点的坐标和各个地点的名称。
在以上三个步骤中，步骤（1）十分关键，选择一个适当的参照点为原点尤为重要。原点的选取，x轴，y轴的确定，直接影响着计算的繁简程度，所以建立直角坐标系时，要以能简捷地确定平面内点的坐标为原则。
6、用坐标表示平移
在平面直角坐标系中，将点（x，y）向右（或向左）平移a个单位长度，可以得到对应点（x+a，y）（或（x-a，y））；将（x，y）向上（或向下）平移b个单位长度，可以得到对应点（x，y+b）（或（x，y-b））。
7、在坐标平面内，求三角形的面积。
（1）用坐标表示点到x轴（或y轴）的距离。
若点P的坐标为（a，b),则点P到x轴的距离为 ，点P到y的距离为 。
（2）用坐标表示x轴（或y轴）上两点间的距离。
已知两点P1(x1,0) 、P2(x2,0),则它们之间的距离P1P2= ；
已知两点M1(0,y1)、 M2（0，y2），则它们之间的距离M1M2＝ 。
3.用坐标表示与x轴平行（或垂直）的线段长。
已知三点P1(x1,y1) 、P2(x2,y2), 、P3(x3,y3).
（1）若P1P2∥x轴，则P1P2=，
（2）若P1P3⊥x轴，则P1P3= 。
例题解析：
 1、
(1)如图是一台雷达探测器测得的结果，图中显示，在ABCDE处有目标
出现。试用适当方式分别表示每个目标的位置.
(2)在直角坐标系中，A点的位置是（3，－2），B点的位置是
（－5，－2），则连接A、B两点所成的线段与_________平行.
(3)若点P的坐标为（a＋3,2a－4）,且P在x轴上，则a＝___________；
若P在y轴上，则a＝___________.
(4)已知点A(x,y).(1)若xy＝0，则点A在___________；(2) 若xy＞0，
则点A在___________；(3)若xy<0，则点A在___________.
(5)点P(－3,5)到x轴的距离为__________，到y轴的距离为_________.
(6)点P到x轴的距离为3，到y轴的距离为4，点P的坐标是_______________________.
(7)若P(a,b)在第四象限，则点P到x轴的距离是____________.
(8)已知点P(2－a,3a－2) 到两轴的距离相等，求P点坐标.
解：
(1)略；
(2)x轴；
(3)2；－3；
(4)坐标轴上；一、三象限；二、四象限；
(5)5；3；
(6)（4，3），（－4，3），（－4，－3），（4，－3）；
(7)－b；
(8)（1，1）或（2，－2）。
2、
(1)在平面直角坐标中，点A（1,2）平移后的坐标是A＇（－3,3），按照同样的规律平移其它点，
则（ ）变换符合这种要求.
A.（3，2）→（4，－2） B.（－1，0）→（－5，－4）
C.（2.5， ）→（－1.5， ） D.（1.2，5）→（－3.2，6）
(2)线段AB的两个端点坐标为A（1,3）、B（2,7），线段CD的两个端点坐标为C（2,－4）、D（3,0），
则线段AB与线段CD的关系是（ ）
A.平行且相等 B.平行但不相等 C.不平行但相等 D. 不平行且不相等
(3)将点P（ ,－5）向左平移 个单位，再向上平移4个单位后得到的坐标为 .
(4)将点P（m－2，n＋1）沿x轴负方向平移3个单位，得到 (1－m，2)，求点P坐标.
(5)已知长方形ABCD中，A（－4,1），B（0,1），C（0,3），求点D的坐标.
解：
(1)C；
(2)A；
(3)（2，－1）；
(4)（1，2）；
(5)（－4，3）.
3、已知：A（-5，4）、B（-2，-2）、C（0，2），求三角形ABC的面积。
分析：为了充分利用x轴与y轴互相垂直于原点O这个性质，可分别作AD⊥y轴于D点，作BE⊥y轴E点，则AD=5，BE=2，CD=2，EC=4，ED=6。
解：△ABC的面积＝梯形ABED的面积－ △CBE的面积－ △ACD的面积
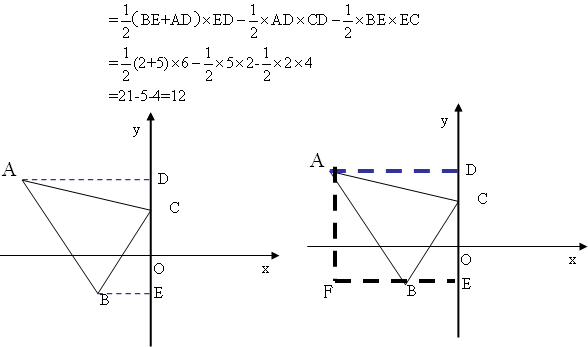
还可以这样解，
作AD⊥y轴于D点，过B点作FE ⊥y轴于E点，过A点作AF ⊥x轴，
则四边形AFED是长方形，AD＝5, CD＝2，EC=4,FB=3, BE=2.
△ABC的面积＝长方形AFED的面积－ △AFB的面积－ △CBE的面积－ △ACD的面积
|
