|
一、和差倍分问题
 1、甲队人数原为乙队人数的2倍,若从甲队调10人到乙队,则甲队人数比乙队人数的一半多3人,求原来两队的人数。 1、甲队人数原为乙队人数的2倍,若从甲队调10人到乙队,则甲队人数比乙队人数的一半多3人,求原来两队的人数。
解:设甲队原有x人,乙队原有y人。
依题意可列方程组:
解这个方程组得:
答:甲队原有24人,乙队原有12人。
 2、一个两位数,十位上的数字比个位上的数字小1,十位上的数字与个位上的数字的和是这个两位数的 2、一个两位数,十位上的数字比个位上的数字小1,十位上的数字与个位上的数字的和是这个两位数的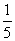 ,求这个两位数是多少? ,求这个两位数是多少?
解:设十位数字是x,个位数字是y
依题意可列方程组: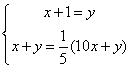
解这个方程组得: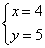
答:这个两位数是45。
 3、某厂为某学校生产校服,已知每3米长的某种布料可以做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用750米长的这种布料生产校服,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套? 3、某厂为某学校生产校服,已知每3米长的某种布料可以做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用750米长的这种布料生产校服,应分别用多少布料生产上衣和裤子才能恰好配套?共能生产多少套?
解:设用x米做上衣,y米做裤子。
依题意可列方程组: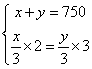
解这个方程组得: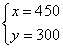
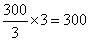 (套) (套)
答:用450米布料做上衣,用300米做裤子恰好配套。共能生产300套。
 4、学生90人编成三组参加义务劳动,甲组与乙组人数比为3:2,乙组与丙组人数的比为7:5,问各组有多少人? 4、学生90人编成三组参加义务劳动,甲组与乙组人数比为3:2,乙组与丙组人数的比为7:5,问各组有多少人?
解法一:设甲组x人,乙组y人,则丙组(90-x-y)人。
依题意可列方程组: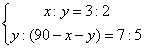
解这个方程组得: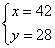
90-42-28=20(人)
答:甲组42人,乙组28人,丙组20人。
解法二:将条件“甲组与乙组人数比为3:2,乙组与丙组人数的比为7:5”中的比例化为“通比”,
即3:2=21:14,7:5=14:10,于是甲乙丙三组人数之比为21:14:10
设甲组21k人,乙组14k人,丙组10k人。
依题意可列方程:21k+14k+10k=90,k=2
 (人) (人)
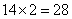 (人) (人)
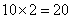 (人) (人)
答:甲组42人,乙组28人,丙组20人。
 5、一个长方形的长增加6厘米,宽减少2厘米,则面积增加8平方厘米,如果长减少6厘米,宽增加6厘米,则面积不变,求原来长方形的周长和面积。 5、一个长方形的长增加6厘米,宽减少2厘米,则面积增加8平方厘米,如果长减少6厘米,宽增加6厘米,则面积不变,求原来长方形的周长和面积。
解法一:设长x厘米,宽y厘米,依题意有:
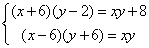
拆掉括号后发现每个等式两边都有 项,抵消掉后得: 项,抵消掉后得:
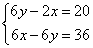
解这个方程组得: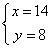
所以原长方形的周长为:2(14+8)=44cm, 面积为:14*8=112cm2
答:长方形周长44cm,面积112cm2
解法二:仔细分析第二个面积不变的条件,
由于面积不变,所以少了的面积等于多出的面积,如图
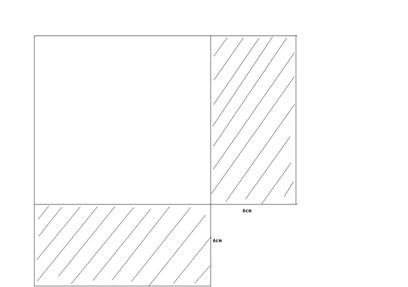
从而空白处为正方形,所以长宽之差为6。
设宽为x厘米,则长为(x+6)厘米。
再由第一个条件比较,少了的一块儿跟多出部分的差,
可得一元一次方程: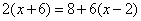
解得x=8
8+6=14(厘米)
所以原长方形的周长为:2(14+8)=44cm, 面积为:14*8=112cm2
答:长方形周长44cm,面积112cm2
二、行程问题:
 1、轮船在两个码头之间航行,顺流航行需6小时,逆流航行要8小时,水流速度为3千米/时,求轮船在静水中的速度及两码头之间的距离。 1、轮船在两个码头之间航行,顺流航行需6小时,逆流航行要8小时,水流速度为3千米/时,求轮船在静水中的速度及两码头之间的距离。
解:设船在静水中的速度为x千米/小时,两码头之间的距离为y千米。
依题意可列方程组: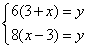
解这个方程组得: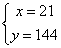
答:船在静水中的速度为21千米/小时,两码头之间的距离为144千米。
 2、甲乙二人练习赛跑,若甲让乙先跑12米,甲跑6秒钟,即可追上乙,若乙比甲先跑2.5秒,则甲跑5秒钟就能追上乙;问甲、乙两人每秒各能跑多少米? 2、甲乙二人练习赛跑,若甲让乙先跑12米,甲跑6秒钟,即可追上乙,若乙比甲先跑2.5秒,则甲跑5秒钟就能追上乙;问甲、乙两人每秒各能跑多少米?
解:设甲的速度为x米/秒,乙的速度为y米/秒。
依题意可列方程组: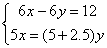
解这个方程组得:
答:甲的速度为6米/秒,乙的速度为4米/秒。
 3、已知某一铁桥长1000米,现有一列火车从桥上通过,测得火车从开始上桥到完全过桥共用1分钟,整列火车完全在桥上的时间是40秒,求火车的速度和长度。 3、已知某一铁桥长1000米,现有一列火车从桥上通过,测得火车从开始上桥到完全过桥共用1分钟,整列火车完全在桥上的时间是40秒,求火车的速度和长度。
解:设火车的速度为x米/秒,车长y米。
依题意可列方程组:
解这个方程组得:
答:火车的速度为20米/秒,车长200米。
 4、一条公路,从甲地到乙地是下坡,从乙地到丙地是平路,一人骑车以12千米/小时的速度下坡,而以9千米/小时的速度通过平路,到达丙地,共用55分钟,回来时,又以8千米/小时的速度行至乙地,以每小时4千米的速度由乙地到达甲地,共用1.5小时,问从甲地到丙地共有多少千米? 4、一条公路,从甲地到乙地是下坡,从乙地到丙地是平路,一人骑车以12千米/小时的速度下坡,而以9千米/小时的速度通过平路,到达丙地,共用55分钟,回来时,又以8千米/小时的速度行至乙地,以每小时4千米的速度由乙地到达甲地,共用1.5小时,问从甲地到丙地共有多少千米?
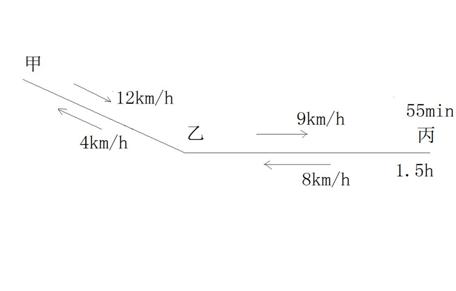
解法一:设甲乙段路程为x千米,乙丙段路程为y千米,
由时间条件可得:
整理得:
解之得: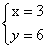
3+6=9(千米)
答:甲丙段共9千米。
解法二:由于下坡和上坡的速度比为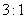 ,所以时间比为 ,所以时间比为 , ,
设甲到乙的时间为x小时,则乙到甲的时间为3x小时;
由题意,乙到丙的时间为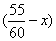 小时,丙到乙的时间为 小时,丙到乙的时间为 小时, 小时,
而平路往返路程相等,
则: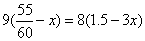
解得
甲乙路程: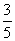 (千米) (千米)
乙丙路程: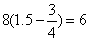 (千米) (千米)
全程:3+6=9(千米)
答:甲丙段共9千米。
 5、某人步行速度为10千米/小时,骑自行车速度为30千米/小时,他从甲地到乙地的 5、某人步行速度为10千米/小时,骑自行车速度为30千米/小时,他从甲地到乙地的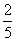 路程步行, 路程步行,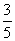 路程骑车,然后按照原路返回时的 路程骑车,然后按照原路返回时的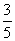 的时间骑车, 的时间骑车,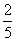 的时间步行,结果比去时快了半小时,求甲乙两地的距离。 的时间步行,结果比去时快了半小时,求甲乙两地的距离。
解:设距离为x千米,返回时间y小时。
依题意可列方程组: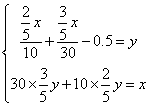
解这个方程组得: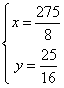
答:甲乙两地距离是 千米。 千米。
三、销售问题
(1)进价:购进商品时的价格(有时也叫成本价)。
(2)售价:在销售商品时的售出价(有时称成交价,卖出价)
(3)标价:在销售时标出的价(有时称原价,定价)
(4)利润:在销售商品的过程中的纯收入, 利润 = 售价 – 进价
(5)利润率:利润占进价的百分率,即利润率 = 利润 ÷进价×100%
(6)打折:卖货时,按照标价乘以十分之几或百分之几十,则称将标价进行了几折;或理解为:销售
价占标价的百分率。例如某种服装打8打即按标价的百分之八十出售。
四、选学内容
 1、某商场有一部自动扶梯匀速由下向上运动,甲、乙二人都急于上楼办事,因此在乘扶梯的同时匀速登梯,甲登了55级后到达楼上,乙登梯速度是甲的2倍(单位时间乙登楼梯级数是甲的2倍),他登了60级后到达楼上,问由楼下到楼上自动扶梯共有多少级? 1、某商场有一部自动扶梯匀速由下向上运动,甲、乙二人都急于上楼办事,因此在乘扶梯的同时匀速登梯,甲登了55级后到达楼上,乙登梯速度是甲的2倍(单位时间乙登楼梯级数是甲的2倍),他登了60级后到达楼上,问由楼下到楼上自动扶梯共有多少级?
解:设甲速度为x级/单位时间,则乙速度为2x级/单位时间,
设扶梯自身速度为y级/单位时间,扶梯共z级台阶。
依题意可列方程组: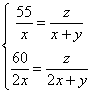
整理得:
于是: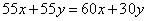
推出: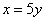
把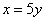 代入 代入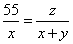 得:z=66 得:z=66
答:扶梯共66级。
|