1.解方程组:
1)
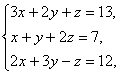 2)
2)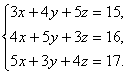
3)
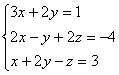 4)
4)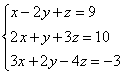
5)
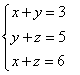 6)
6)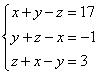
2.已知:y=ax2+bx+c,当x1=1时,y1=-1;当x2=0时,y2=1,当x3=-1时,y3=13.
1)求a、b、c的值;
2)当x=-2时,求y的值.
3.若x1, x2, x3, x4和x5满足方程组
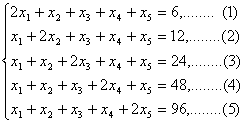 ,试确定3x3+2x4-x5的值.
,试确定3x3+2x4-x5的值.参考答案:
1. 1)
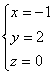
4)
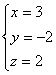 5)
5)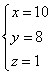
2.1)a=5,b=-7,c=1,即y=5x2-7x+1;
2)当x=-2时,y=35.
3.
解:(1)+(2)+(3)+(4)+(5),得6(x1+x2+x3+x4+x5)=186,
即x1+x2+x3+x4+x5=31, (6)
(3)-(6),得x3=-7
(4)-(6),得x4=17
(5)-(6),得x5=65.
∴ 3x3+2x4-x5=-21+34-65=-52.
