学法指导：
这一部分知识与小学知识联系密切，大多数图形、概念在小学都接触过，但小学的要求是能区分直线、射线、线段的概念并体会它们的一些性质，层次要求较低。本章是空间与图形的起始章，涉及的概念比较多，许多概念之间都有着密切的联系和区别，把握了这些联系和区别，就能更好的理解这些概念。例如，直线、射线、线段三个概念联系密切，它们都是直的，正是因为此，在以后讲平行、垂直时，定义了直线与直线平行、垂直后，就不再定义直线与射线、线段的平行、垂直了；同时它们之间又有区别，端点个数不同，因而长度有有限与无限之分。对于作图能力的要求，在教科书上已经给出了作一条线段等于已知线段。同时，要注意概念的定义和性质的表述，逐步懂得几何语句的意义并能建立几何语句与图形之间的联系。这些不仅是学习好本节的关键，同时对于学好以后各节也是很重要的。
知识点讲解：
一、直线
1．直线的概念
（1）点和直线都是几何学的基本（或原始）概念、不定义．
直线是向两个方向无限延伸的．
（2）点的表示：用一个大写字母
例如：点A、点P
（3）直线的表示：用一个小写字母或用直线上两个点表示
例如：直线l、直线AB
2．点与直线的位置关系
（1）点与直线有两种位置关系，即点在直线外（或称直线不经过这个点）及点在直线上（或称直线经
过这个点）．
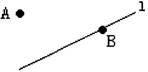
（2）“点A在直线l上”等价说法“直线l经过点A”，
“点A在直线l外”等价说法“直线l不经过点A”，
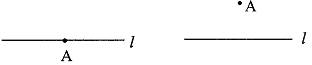
（3）“点A在直线l外”分为两种情形：
①点在直线l的上侧
②点A在直线l的下侧
3．直线的特性
直线的本质属性是用公理给出的，即：经过两点有一条直线，并且只有一条直线．简称“两点确定一条直线”．
对比：经过A、B两点的直线有一条（存在性），且只有一条（唯一性）；
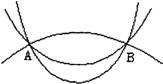
经过A、B两点的曲线有（存在）一条，但不唯一．
4．两条直线的位置关系
（1）在同一平面内，两条不同的直线可能没有公共点，这时称这两条直线平行；两条不同的直线如果
有公共点，只能有一个公共点，这时称这两条直线相交．这是因为：在同一平面内假设两条不同
的直线有两个公共点，这样过这两点有两条不同的直线，与直线公理矛盾。所以假设错误。因此
两条不同的直线最多只能有一个公共点。
（2）在空间，两条不同的直线的位置除了平行、相交以外，还有异面，如图所示
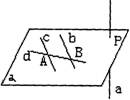
二、射线
1．在直线上的一点和它一旁的部分叫做射线，这一点叫做射线的端点．
2．射线用一个小写字母或用端点和射线上另一个点表示
例如：射线l、射线AB（左边字母为射线端点）
三、线段
1．定义：
直线上两个点和它们之间的部分叫做线段，这两点叫做线段的端点。
2．表示方法：
线段用一个小写字母或用线段的两个端点的字母表示， 例如：线段l、线段AB
3．直线、射线、线段的区别：
| 图形 | 端点个数 | 延伸方向个数 | 长度 | |
| 直线 |  |
0个 | 2个 | 无限 |
| 射线 |  |
1个 | 1个 | 无限 |
| 线段 |  |
2个 | 0个 | 有限 |
4. 直线、射线、线段的联系：
射线、线段的概念是利用直线来定义的，它们都是直线的一部分，其中线段是直线的有限部分．
5．线段的性质
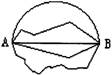
线段的性质也是用公理给出的即线段公理：在所有连接两点的线中，线段最短。连结两点线段的长度叫做这两点间的距离。用这条线段的长度定义距离的合理性表现在线段公理保证了这样的线段是唯一的并且是长度最短的。
6．线段的度量
（1）直接用刻度尺或圆规和刻度尺结合使用
（2）表示法：AB=7cm
7．线段长短的比较
（1）重叠比较法：一端重合，观察另一端位置
例如：
∴ AB<CD
（2）数量比较法：用刻度尺量出长度，将长度进行比较
8．线段的和差及画法
例：已知：如图，线段a和线段b
求作：线段AB和线段CD，使得AB=a+b，CD=a-b
作法：（1）作射线AN，在射线AN上顺次截取AP=a，PB=b，则线段AB即为所求；
（2）作射线CM，在射线CM上截取CA=a，在线段CA上反向截取AD=b，则线段CD即为所求。
9．线段的画法的书写要求
例1：已知：点A、B
求作：（1）在A，B两点间画一条线段，画法说成“连结AB”。
（2）经过A，B两点画一条直线，画法说成“过A，B两点作直线”或“作直线A，B”。
（3）作射线以A为端点，而经过B点，画法说成“作射线AB”。
（4）作线段AB的延长线，画法说成“延长线段AB”或“反向延长线段BA”。
（5）线段AB的延长线，使它和直线CD交于O点,画法说成“延长线段AB，使它和直线CD交于O点”
（6）作射线AB的反向延长线，画法说成“反向延长射线BA”
例2：已知：线段a，b
求作：（1）AB=a； （2）AB=2a；（3）AB=2a-b
画法：（1）1．画射线AC．
2．在射线AC上截取AB=a．
线段AB就是所要画的线段．
（2）1. 画射线AD．
2．在射线AD上顺次截取AC=CB=a．
线段AB就是所要画的线段．
（3）1．画射线AE；
2．在射线AE上顺次截取AC=CD=a；
3．在线段AD上截取DB=b．
线段AB就是所要画的线段．
10．线段的中点：
将一条线段分成两条相等的线段的点，叫做这条线段的中点。
∵ 点C是线段AB的中点．
∴ AB=2AC，AB=2CB；AC=CB；AC=
AB，CB=AB 
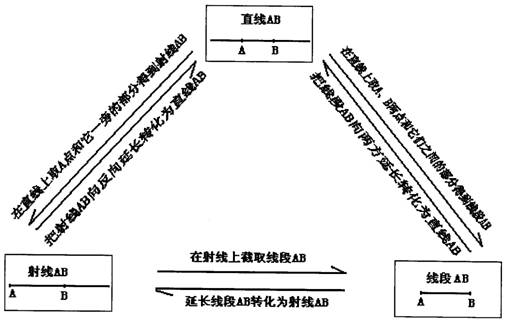
11. 知识体系图：
经典例题：
一、数条数或个数
1．（1）过两点可以画几条直线?过三点呢?过四点呢?答案：1；1或3；1或4或6
（2）平面上有n个点，其中每三个点都不共线，共可以画多少条直线?
答案：
（3）两条直线相交，有几个交点？三条直线呢？四条直线呢？
答案： 1；1或3；1或4或6
（4）n条直线两两相交，有几个交点？
答案：
（5）一条直线上有n个点时，以这些点为端点的射线、线段有多少条?
答案：
；二、线段和差倍分的计算
2．如图，已知C为AB中点，D为BC的中点，BD=6cm，求AB的长．
解：∵ D为BC中点
∴ BC=2BD
∵ BD=6cm
∴ BC=12cm
∵ C为AB中点
∴ AB=2BC=24cm
3．如图，已知线段AD=6cm，线段AC=BD=4cm，E、F分别是线段AB、CD的中点，求EF．
解：∵ AC=BD
∴ AD-BD=AD-AC 即AB=CD=6-4=2
∵ E、F分别是线段AB、CD的中点
∴ AE=
AB=1 FD=CD=1∴ EF=AD-AE-FD=6-1-1=4（cm）
注：简单的等式性质和等量代换应该有所涉及。
4．已知AB=8cm，在直线AB上有一点C，且BC=4cm，M是线段AC的中点，求线段AM的长．解：（1）当点C在线段AB上时，如下图：
AC=AB-BC=8-4=4
∵ M是AC中点，
∴ AM=
AC=2（cm）。（2）当点C在线段AB的延长线上时，如下图：
AC=AB+BC=8+4=12
同理，∴ AM=
AC=6（cm）三、代数方法解决几何问题
5．如图，
B、C两点把线段AD分成4：5：7三部分，若CD=14cm，
求：AD的长。
解：∵ B、C两点把线段AD分成4：5：7三部分
∴ 设AB=4k，BC=5k，CD=7k，
∵ CD=14cm
∴ 7k=14，解得k=2
∴ AD=AB+BC+CD=4k+5k+7k=16k=32（cm）
注：强调用代数方法解决几何问题的思路及规范表述。
6．如图，延长线段AB到C，使BC=AB，D为AC的中点，DC=2，求AB的长。
解：设AB长为x，由BC=
AB，得BC=
∵ D为AC的中点，DC=2，
∴ AC=2DC=4
∵ AB+BC=AC，
∴
解得，
，所以
注：本题也可以不设未知数，直接用线段AB来计算，作用是一样的。初始阶段设未知数相对好理解一点，慢慢过渡到直接用线段列方程计算。
