一、巩固提高
(一)带字母系数的一元一次不等式(组)
带字母系数的一元一次不等式(组)问题相对比较复杂,在中考与数学竞赛中经常遇到,在解决这类问题时,须注意分类讨论。
分析:“对于
解:由
∵
示意图:

∴
∴
分析:我们不妨从会的地方入手,由前面给出的两个关于a、b、c的三元一次方程,可以消去两个未知数,即可用a、b、c中的一个字母表示另两个字母,那么m也可用这个字母表示出来。又由题目已知的a、b、c是三个非负数,可知对于一个字母的三个限制进而得到这个字母的较具体的范围,也就得到了m的范围。
解:由
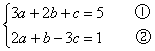
②×2
③-①
代入②
∴
∵
∴
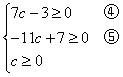
由④
由⑤
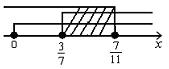
∴
∴
即
∴
∴
解:∵
∴
(1)当
(2)当
(3)当
原式化为
注意:由于不知道

解:由①
(注意:由于不知道a的正负,因而不要随意将系数a除到右边去)
由②
(1)当
(须注意的是,不可以直接写出结果为
∵
∴
∴

∴
(2)当
∵
∴
∴
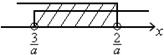
∴
(3)当
此不等式组无解
综上,当
当
当
(二)含绝对值的一元一次不等式(组)
解决这类问题的关键,在于根据绝对值的定义或性质,去掉绝对值符号,将其化为常规的不等式(组),在其中经常使用到的方法,是将数轴分段进行讨论,即使用“零点分段法”以去掉绝对值符号。
分析:这里有两个绝对值,对于多个绝对值的问题,我们一般采用“零点分段法”,即,先确定
解:令
令
即5与-7分别是
(1)
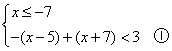
由①
∴不等式组无解
(2)
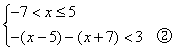
由②,
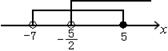
∴
(3)
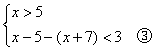
由③
∴
综上,
原不等式的解集为
二、列一元一次不等式(组)解应用题
根据等量关系列方程是我们解应用题的常用方法.但有的应用题中的数量是不等关系,我们可以仿照列方程的方法,根据题目中的不等关系列出不等式也可使问题得解.
解:设他答对x道题
据题意,列10x-5(20-x)>90
10x-100+5x>90
15x>190
∵ x为整数 ∴ x≥13
答:他至少答对13道题。
注意:为什么使用不等式来解决问题?为什么不设他至少答对x道题?
请注意不等式与方程的异同:
(1)不等式自身带不等关系,易于说明;
(2)方程需搭配分析
对比在此问题上运用方程和运用不等式各自的优缺点,从而初步概括归纳运用一元一次不等式解决实际问题的基本思路。
列一元一次不等式组解应用题的一般步骤如下:
1、审:审清题意,弄懂已知什么,求什么,以及各个数量之间的关系。
2、设:只能设一个未知数,一般是与所求问题有直接关系的量。
3、找:找出题中所有的不等关系,特别是隐含的数量关系。
4、列:列出不等式组。
5、解:分别解出每个不等式的解集,再求其公共部分,得出结果。
6、答:根据所得结果作出回答。
(1) 用含x的代数式表示m;
(2) 求出该校的获奖人数及所买课外读物的本数.
解:
(1) m=3x+8,
(2)依题意,得0≤3x+8-5(x-1)<3
0≤-2x+13<3
-13≤-2x<-10
∵x为正整数,∴ x=6.
把x=6代入m=3x+8, 得m=26.
答:该校获奖6名,购买26本课外读物.
注意:当问题要求取所列不等式的正整数解时,答案就可能变得具体、唯一.
分析:在能构建不等式的题目中往往有表示不等关系的词语,如大于、小于、不大于、不小于、超过、不超过等。我们只有先找到这些关键信息,才能列出正确的不等式组。本题数量关系不算复杂,根据题意可直接列出两个不等式构成不等式组。
解:设可能有x间宿舍,则有(4x+19)名学生
据题意,列
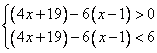

∴
∴ 当房间有10间时,人数为59人.
∴ 当房间有11间时,人数为63人.
∴ 当房间有12间时,人数为67人.
