教学目标:
1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检
验结果”的过程,体会方程组是刻画现实世界中含有多个未知数的问题的数学模型.
2.了解二元一次方程组及其相关概念,能设两个未知数,并列方程组表示实际问题中的两种相关的等
量关系.
3.了解解二元一次方程组的基本目标:使方程组逐步转化为x=a,y=b的形式,体会“消元”思想,掌
握解二元一次方程组的代入法和加减法,能根据二元一次方程组的具体形式选择适当的解法.
4.了解三元一次方程组及其解法,进一步体会“消元”思想,能根据三元一次方程组的具体形式选择
适当的解法.
5.通过探究实际问题,进一步认识利用二(三)元一次方程组解决问题的基本过程,体会数学的应用价
值,提高分析问题、解决问题的能力.
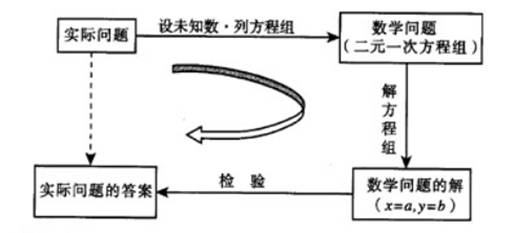
教学内容解析:

练习题:
练习一
1.在下列各式中①5x-y+3; ②xy+y=8; ③2x+5=0; ④
⑥2x+3y=4+2x; ⑦x2+x=2x2-(x2+y),是二元一次方程的有( ).
A.2个 B.3个 C.4个 D.5个
2.判断下列方程组是否是二元一次方程组,并说明理由.
(1)
3.下列结论正确的是( )
A.方程
B.方程
C.方程组
D.方程组
4.判断下列两组数值是否是方程组
(1)
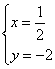 (2)
(2)5.已知
6.已知
7.已知
8.已知关于x、y的二元一次方程组
9.已知
练习二
1.若
2.已知
3.
4.解方程组
5.解方程组
6.解方程组
7.解方程组
8.解方程组
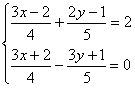
9.解方程组:
10.方程组
11.已知方程组
练习三
1.
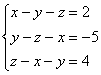 2.
2.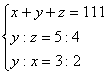
3.
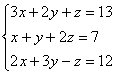 4.
4.
5.
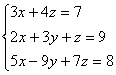 6.
6.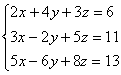
7.已知:2x-3y-z=0 ,x+3y-14z=0且x、y、z不全为0,求
8.如果方程组
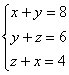 的解使代数式kx+2y-z的值为10,求k的值.
的解使代数式kx+2y-z的值为10,求k的值.9.三个同学对问题“若方程组
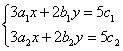 的解.”
的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规
律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方
法来解决”.参考他们的讨论,你认为这个题目的解应该是____________.
10. 一个布袋中装有红、黄、蓝三种颜色的大小相同的木球,红球上标有数字1,黄球上标有数字2,
蓝球上标有数字3,小明从布袋中摸出10个球,它们上面所标数字的和等于21,则小明摸出的球中
红球的个数最多不超过______.
练习四
1.已知一个两位数,它的个位数字比十位数字大3,若将这个两位数的个位数字和十位数字对调,则得
到的新数与原数的和为99,求这个两位数.
2.用白铁皮做罐头盒,每张铁皮可制盒身16个,或制盒底43个,一个盒身与两个盒底配成一套罐头盒
,现有150张白铁皮,用多少张制盒身、多少张制盒底,可以正好制成整套罐头盒?
3.买甲、乙两种纯净水共用去250元,其中甲种水每桶8元,乙种水每桶6元,并且乙种水的桶数是甲种
水的桶数的75%. 问:甲、乙两种纯净水各买了多少桶?
4. 一项工程,甲队单独做要12天完成,乙队单独做要15天完成,丙队单独做要20天完成,按原计划,
这项工程要在7天内完成,现在甲、乙两队先合做若干天,以后为加快速度,丙队也同时加入了这项
工作,这样比原计划提前一天完成,问:甲、乙两队合做了多少天?丙队加入后又做了多少天?
5.甲乙两码头相距60千米,某船往返两地,顺流时用3小时,逆流时用3小时45分,求船在静水中的速
度及水流的速度.
6.A、B两地之间的路为20千米,甲从A地,乙从B地同时出发,相向而行,2小时后在C点相遇,相遇后
甲原速返回A地,乙仍向A地前进,甲返回到A时,乙离A地还有2千米,求甲、乙两人的时速.
7.在“十一”旅游黄金周期间,某超市打折促销.已知A商品7.5折销售,B商品8折销售.买20件A商品与
10件B商品,打折前比打折后多花460元.打折后买10件A商品和10件B商品共用1090元.求A、B商品打折
前的价格.
8.学校的篮球数比排球数的2倍少3个,足球数与排球数的比是2:3,三种球共41个,求三种球各有多
少 ?
9. 学校举办“迎奥运”知识竞赛,设一、二、三等奖共12名,奖品发放方案如下表
| 一等奖 | 二等奖 | 三等奖 |
| 1盒福娃和1枚徽章 | 1盒福娃 | 1枚徽章 |
息:
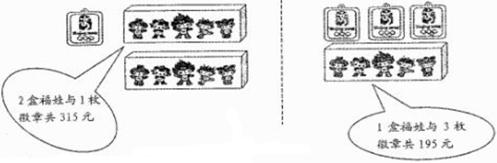
(1)求一盒“福娃”和一枚徽章各多少元?
(2)若本次活动设一等奖2名,则二等奖和三等奖应各设多少名?
10.足球比赛记分规则如下:胜1场得3分,平1场得1分,负1场得0分.某球队已参加了12场比赛,得
21分,请你判断该队胜、平、负各几场.
参考答案:
练习一
1.A 2.解:(1)不是;(2)是;(3)是 3. D
4. 解:(1)不是 ,(2)是;
5. a=-1,b=2, (a+b)(a-b)=-3
6. x=4, y=2,
7. a=-2/7, b=8/7, c=11
8. 8
9. 1
练习二
1.x=1,y=5 2.a=2,b=1,2a+b=5 3.a=9,b=-3 4.x=3,y=2
5.x=1/3,y=-3 6.x=6,y=-1/2 7.x=650, y=50 8.x=2 ,y=3
9.x=5, y=3 10.m=-5 11.a=14,b=2
练习三
1.x=1/2,y=-3,z=3/2 2.x=30,y=45,z=36 3.x=2,y=3,z=1 4.x=10,y=9,z=7
5.x=5,y=1/3,z=-2 6.x=-16,y=1/2,z=12 7.26/23 8.k=1/3
9.x=5,y=10 10. 4
练习四
1.36; 2. 身:86,底:64 ; 3. 甲:20,乙:15 ;
4. 甲乙合做:4,丙:2 ; 5. 静:18 水:2; 6.甲:5.5 乙:4.5 ;
7.A:60 B:80; 8. 篮球:21, 排球:12, 足球:8;
9.解:(1)答:一盒“福娃”150元,一枚徽章15元.
(2)设二等奖
10. 解:设该队胜x场,平y场,则由已知得
 由①知y=21-3x代入②,得x+21-3x≤12.∴x≥
由①知y=21-3x代入②,得x+21-3x≤12.∴x≥又y≥0,由①知3x≤21.∴x≤7.即
又x为整数,∴x=5,6,7.故
答:该队胜5场,平6场,负1场;或胜6场,平3场,负3场;或胜7场,平0场,负5场.
