|
巧记硬背学数学
适用对象:学习数学有困难的同学。
诊病开方:
数学中有不少知识是需要熟记的,经实战检验较有效的硬背巧记方法有:数码法、列表法、图形法、联想法、“备忘录”法和谐音法等。
众所周知,数学是一门研究数和形的科学,中学数学各章节各分科的内容都是依从于一个概念到另一个概念,一个关系到另一个关系的推演。学习数学就是要学会通过逻辑推理或运算来沟通问题的假设条件和结论,而其基础就是要充分并恰当地借助有关数学的重要定理、公式、法则和基本成题。为此必须牢固记忆重要定理、公式和法则,因为公式、定理和法则是反映数字对象属性之间关系的,只有概念清晰,定理和公式、法则熟悉才有正确的思维基础,才能形成推理论证的能力和运算的技能技巧。
那么,怎样才能记住众多的数学定理、公式、法则呢?从中学教学实践看,有一些内容可以巧记,但有些内容恐怕只有硬背了。归纳起来,大致有以下一些方法。
一、数码法
即将相关知识用数码进行编组的方法。例如:小结三角基础知识时用“一、二、三、四、……”编号。数码可用自然数,也可用特征数码。如:
一组推广:锐角三角函数→任意角三角函数。
二类问题:①求值:给角求值与给值求值问题。②求角:给值求角与三角方程问题。
三套公式:同角公式、诱导公式、加法定理。
四个图像:正弦、余弦、正切、余切函数图像和性质。
二、列表法
例如,上海市第一中学的俞琤同学,便是一位善于利用此法的高手。他说:我在学数学时,常常运用列表的方法来加深自己对某些概念的印象。例如,学习代数中的函数部分,我用下表来归纳指数和对数函数的性质与关系:
| |
指数函数 |
对数函数 |
性
质 |
a>1 |
0<a<1 |
a>1 |
0<a<1 |
1)y>0
2)x=0时y=1 |
|
1)x>0
2)x=1时y=0 |
|
3)x>0时y>1
x<0时0<y<1
4)是增函数 |
x>0时0<y<1
x<0时y>1
是减函数 |
3)x>1时y>0
0<x<1时y<0
4)是增函数 |
x>1时y<0
0<x<1时y>0
是减函数 |
| 关系 |
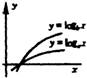
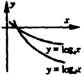
互为反函数 | 在此表中,我把两种函数的关系作了确定。根据对数函数的性质,我又得出了下图:
| 图形 |
 |
 |
 |
| 底数大小 |
a>b>1 |
0<c<d<1 |
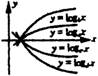
a>b>1>d>c>0 | 图中(一)和(二)是我在实际作图时发现的规律,之后我又得出了图中(三)的规律,把不同类型的对数函数的底数大小作了确定。
俞琤同学说,学习几何时,也应多多列表,几何论证定理的文字太多,全部归入表中很费时间。在列表时不妨作一些改动,比如有一条证明三角形全等的定理为:在两个三角形中,如果它们的两个角和一条夹边对应相等,那么这两个三角形全等。这句话要很快理解并不容易,可用字母和等式来代替条件,定理就变为:△ABC和△DEF中,如果AB=DE,∠A=∠D,∠B=∠E,那么△ABC全等于△DEF。这样一来,定理便简明易懂,还可节省学习时间。
俞琤同学说:“表列好后,还应经常翻阅。只在考试前临时抱佛脚地看一下是不会有多大作用的。最好是每天在做作业前看一遍,这样可以及时回顾以前学过的内容,理清头绪,减少作业的错误。还可将当天的上课内容补充进表中,倘若练习中出现了一些典型题例,也要补充进去。”
三、图形法
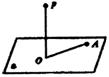
例如画出立体几何定理的图形,回忆定理的条件和结论。
(1)线面平行判定定理
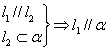 
(2)线面平行性质定理
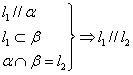 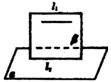
(3)线面垂直判定定理
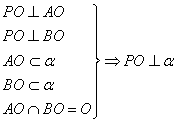 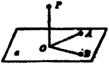
(4)线面垂直性质定理
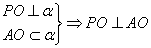 
四、联想法
靠联想来启发记忆,加强记忆,可用性状接近联想和关系对比联想。
例如:从等差数列的通项公式和前n项和公式联想等比数列;从等比数列前n项和公式联想无穷递缩等比数列各项和。又如从平面几何联想到立体几何:平面几何中讲到“直线上的一点只能作一条直线和已知直线垂直。”但在立体几何中就不是这样,等等。
五、“备忘录”法
随身带一个小本本,将易遗忘的公式摘录备查,把自己的小结记录备用,把典型成题和解题方法摘抄整理,把自己易错的概念和作业订正记载,引以为戒……
六、谐音法
在数学计算中,有一些数据是常用的、必记的。可这些数据又没有什么规律,很不好记。为此,云南省一些重点学校的教师想到了谐音记忆法:利用谐音,自编口诀,以帮助自己记住一些常用的数据。实战效果非常好。例如:
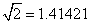 意(1)思(4)意(1)思(4)而(2)已(1) 意(1)思(4)意(1)思(4)而(2)已(1)
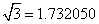 一(1)起(7)扇(3)儿(2)灵(0)不(5)灵(0) 一(1)起(7)扇(3)儿(2)灵(0)不(5)灵(0)
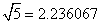 量(2)量(2)山(3)路(6)领(0)路(6)去(7) 量(2)量(2)山(3)路(6)领(0)路(6)去(7)
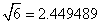 粮(2)食(4)是(4)酒(9)是(4)白(8)酒(9) 粮(2)食(4)是(4)酒(9)是(4)白(8)酒(9)
 山(3)巅(.)一(1)狮(4)一(1)虎(4)救(9)二(2)牛(6) 山(3)巅(.)一(1)狮(4)一(1)虎(4)救(9)二(2)牛(6)
log2=0.3010 老哥二(log2)藏在山(3)岭(0)一(1)洞(0)里
log3=0.4771 老哥三(log3)带领(0)司(4)机(7)起(7)义(1)
谐音助记法在英语、语文乃至历史、地理等学科中,运用较广,但似乎很少有人将这一方法用在数学中。这大概是因为许多人认为数学要记的主要是一些公式,而公式是不宜用谐音助记法来帮助记忆的。岂不知数学中除了公式外,还有大量常用数据需要记忆。
1997年高考云南省理工科状元朱寰同学就曾颇有感触地说:“平时多注意记一点常数,如原子量之类的,到时可以大大提高计算速度而且节约时间。”然而这些数据不像公式,无任何逻辑可言,又要求准确记忆,实在让人头疼。据江苏省某县重点中学对历届作弊学生的统计,其中约23%是因记不住某一数据而违纪翻阅课本、笔记。可见在学习数学的时候,重点数据的记忆是一个不容忽视的大问题。这些重点数据,不恰恰是可以用谐音助记法来记忆的吗?
专家点评:
很多人可能认为文科的学习需要记忆,而理科则不必去记。然而事实并非如此,文科需要记忆自不必说,同样理科也是需要记忆的。这里所说的记并不是单指公式和定理(这当然是要记的),也是指要熟悉各个知识点的考查方法和典型题型。做题多了,大家都会体会到,对于同一个知识点其考查方法往往是类似的,所谓“万变不离其宗”。只要掌握了最根本的内容,无论如何来考,都可以应付自如。这里要记的就是各个知识点基本内容及其常见考查点,如果这些都熟悉了,那么遇到具体题目就是简单地应用而已了。这里说的“记”,实则仍然是在理解中掌握,否则,单凭你去背一道题目,这是无法奏效的。
为什么说学习理科一定得死记硬背一些东西,除了上面已经谈到的以外,在此我们还可再补充三点理由。
第一,中学时代,正是一个人记忆力最好的时候,应趁此多记一些东西。著名数学家陈景润先生在回忆他的中学时代学习生活时就曾说过:“当时我能把数理化的许多概念、公式、定理、定律,一一装进自己的脑海里,随时拈来应用。有一次化学老师要同学们把一本书背下来,同学们都感到很困难,但我却觉得:这一点很容易,多花点功夫就可以记下来,怕什么?果然没几天,我就把全书背诵记牢了。当时我认为,我们青年人,知识面有限,理解能力较差,记忆力特别强,必须背诵许多的知识,将来使用时就会左右逢源,一呼百应,十分得心应手了。”学生时代是我们一生中记忆力最强的时期。我们一定要利用记忆力强的优势,多记多背一些东西。数学自然也不应例外。
第二,有些高考试题就是要求同学们背出定理、公式和法则;有的不过是进而要求推导或证明;有的则是教材中例题或习题的变形。例如1982年高考第四大题(计12分)实际上是统编教材第58页例3。1984年高考第四大题(计12分)即统编教材第二册第99页复习题五中的第一题。1986年高考第三大题(计10分)即统编教材第二册第100页第八题……以上仅是不完全的统计,实际上只有背诵更多的知识,才会左右逢源,一呼百应,得心应手。
第三,为了记忆,有时需要将知识进行整理、归纳。如上述口诀法、数码法、列表法等,便是如此。这实际上就是一种很好的总结和提高。
|