|
一、填空题
1、1 2、(–11, 10) 3、10 4、3n 5、4x+3y–20=0 6、–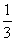 或3 或3
7、8 8、2 9、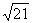 10、 10、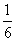 11、 11、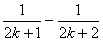
二、选择题
12、D 13、A 14、C 15、B
三、解答题
16、因为在ΔABC中A(–1, –1)、B(5, 5),垂心H(4, –1),AH⊥BC,BH⊥AC,
所以直线AH的斜率为0,则直线BC的斜率不存在,
故BC的方程为:x=5,………………………………………………………2分
直线BH的斜率为6,则直线AC的斜率为 –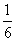 , ,
故直线AC的方程为:y=–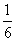 (x+1)–1,……………………………………4分 (x+1)–1,……………………………………4分
令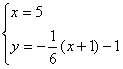 ,………………………………………………………5分 ,………………………………………………………5分
解之得: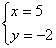 ……………………………………………………………7分 ……………………………………………………………7分
所以C点的坐标为(5,–2) ……………………………………………………8分
17、因为向量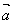 =(1, 2), =(1, 2),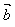 =(x,1), =(x,1),
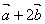 =(1+2x, 4), =(1+2x, 4),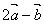 =(2–x, 3) …………………………………………2分 =(2–x, 3) …………………………………………2分
因为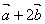 与 与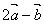 平行,所以 平行,所以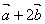 =k( =k(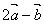 )…………………………3分 )…………………………3分
即: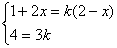 ,所以x= ,所以x=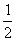 ,………………………………………4分 ,………………………………………4分
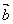 =( =(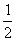 ,1);……………………………………………………………………5分 ,1);……………………………………………………………………5分
(2)已知点A(3 ,–1),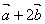 =(2,4),向量 =(2,4),向量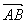 与 与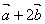 垂直, 垂直,
即直线AB的法向量为(2, 4),………………………………………………6分
所以直线AB的点法向式为2(x–3)+4(y+1)=0,
其一般式方程为x+2y–1=0…………………………………………………8分
18、(1)因为向量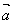 =(x+3, x–2),向量 =(x+3, x–2),向量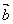 =(1–x, 4),其中0≤x≤5 =(1–x, 4),其中0≤x≤5
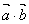 =(x+3)(1–x)+4(x–2)= –x2+2x–5,(0≤x≤5) ……………………………3分 =(x+3)(1–x)+4(x–2)= –x2+2x–5,(0≤x≤5) ……………………………3分
(2) 设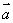 、 、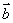 夹角为a, 夹角为a,
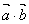 = –x2+2x–5= –(x–1)2–4,(0≤x≤5) ……………………………………4分 = –x2+2x–5= –(x–1)2–4,(0≤x≤5) ……………………………………4分
所以当x=1时,(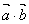 )max= –4,此时x=1,向量 )max= –4,此时x=1,向量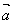 =(4, –1),向量 =(4, –1),向量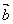 =(0, 4) =(0, 4)
cosa= –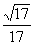 , ,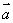 、 、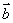 夹角的大小为π–arccos 夹角的大小为π–arccos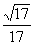 ,……………………6分 ,……………………6分
当x=5时,(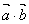 )min= –20,此时x=5,向量 )min= –20,此时x=5,向量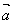 =(8, 3),向量 =(8, 3),向量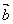 =(–4, 4) =(–4, 4)
cosa= –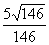 , ,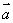 、 、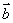 夹角的大小为π–arccos 夹角的大小为π–arccos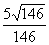 。………………8分 。………………8分
19、D=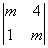 =(m+2)(m–2),Dx= =(m+2)(m–2),Dx=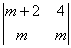 =m(m–2), =m(m–2),
Dy=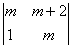 =(m+1)(m–2) …………………………………………………3分 =(m+1)(m–2) …………………………………………………3分
(1)当m ¹ ±2时,D ¹ 0,原方程组有唯一组解,即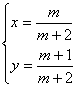 …………6分 …………6分
(2)当m = –2时,D=0,Dx=8 ¹ 0,原方程组无解;………………………8分
(3)当m=2时,D=0,Dx=0,Dy=0,原方程组有无穷组解。……………9分
20、(1)因为a1=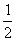 ,an+1= ,an+1=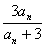 ,所以a2= ,所以a2=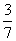 , a3= , a3=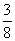 ,a4= ,a4=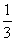 ……………3分 ……………3分
(2)猜测:an=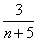 ,…………………………………………………………4分 ,…………………………………………………………4分
(3)当n=1时,a1=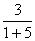 = =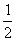 ,等式成立,…………………………………5分 ,等式成立,…………………………………5分
假设当n=k时等式,即:ak=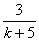 ,………………………………………6分 ,………………………………………6分
则当n=k+1时,ak+1=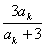 = =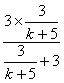 = =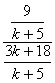 = =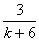 …………………8分 …………………8分
即当n=k+1时,等式也成立,………………………………………………9分
所以由上述可知,等式an=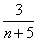 对nÎN*都成立。………………………10分 对nÎN*都成立。………………………10分
21、(1)由于当n≥2时,a2+a3+…+an=2n+p(p为常数),
a2+a3+…+an+an+1=2n+1+p
两式相减得:an+1=2n,因为数列{an}为等比数列,所以a1=1,a2=2,…1分
由条件可得p=–2,an=2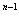 ,(n∈N ,(n∈N );…………………………………2分 );…………………………………2分
(2)因为数列{bn}的前n项和为Sn,b1=2,
n bn+1=Sn+n(n+1),(n–1)bn=Sn–1+(n–1)n
两式相减得:nbn+1–nbn+bn=bn+2n,(n≥2)
bn+1–bn=2,(n≥2),…………………………………………………………4分
即{bn}是从第二项起为公差是2的等差数列,b2=S1+1(1+1)=4
因为b1=2,所以{bn}是公差是2的等差数列,
bn=2n,(n∈N );……………………………………………………………5分 );……………………………………………………………5分
Sn=n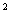 +n;…………………………………………………………………6分 +n;…………………………………………………………………6分
(3)因为Tn=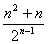 ,若Tn= ,若Tn= 对一切正整数n,均有Tn ≤ C恒成立,则需C大于或等于Tn的最大值,……………………………………………………7分 对一切正整数n,均有Tn ≤ C恒成立,则需C大于或等于Tn的最大值,……………………………………………………7分
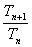 = =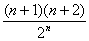 ´ ´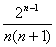 = = , ,
令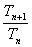 ≥1得:n≤2, ≥1得:n≤2,
即有:T1=2≤T2=3=T3=3≥T4=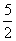 ≥T5= ≥T5=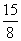 ≥…≥Tn≥…,即数列{Tn}是先增后减的数列,且Tn的极限是0, ≥…≥Tn≥…,即数列{Tn}是先增后减的数列,且Tn的极限是0,
故有Tn的最大值为T2=T3=3,……………………………………………9分
又对一切正整数n,均有Tn≤C恒成立,∴C≥3…………………………10分
|