|
轴对称复习
一、知识点回顾
1.主要概念
轴对称与轴对称图形的联系与区别.
轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称.两个图形关于某直线对称,也称为轴对称.这条直线就是它的对称轴.
轴对称图形:如果一个图形沿一条直线对折,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线就是它的对称轴.
区别:轴对称图形是说一个具有特殊性质的图形,是对一个图形说的;
轴对称是指两个图形之间的位置关系,是对两个图形说的.
联系:轴对称与轴对称图形都有对称轴,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对
称图形;如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成轴对称.
2.重要结论
(1)轴对称性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的____(垂直平分线)
(2)线段垂直平分线的性质:线段垂直平分线上的点与这条线段两个______距离_____(端点,相等)
(3)线段垂直平分线的判定:与一条线段两个端点距离___________的点,在这条线段的
___________(相等,垂直平分线上)
(4)作轴对称图形:几何图形都可以看作由___________组成,只要分别作出这些___________关于对
称轴的对应点,再连接这些对应点,就可以得到原图形的轴对称图形(点,点)
(5)用坐标表示轴对称:点(x,y)关于x轴对称的点的的坐标是__________;关于y轴对称的点的的
坐标是___________((x,-y),(-x,y))
(6)等腰三角形的性质:如果一个三角形有两条___________相等,那么这两条___________所对的角
也相等(简写作“___________”)(边,边,等边对等角)
(7)等腰三角形的判定:如果一个三角形有两个___________相等,那么这两个___________所对的边
也相等(简写成“___________”).(角,角,等角对等边)
(8)等边三角形的性质:等边三角形的三个内角都___________,并且每一个角都等于___________.
(相等,60度)
(9)等边三角形的判定:三个角都___________的三角形就是等边三角形;有一个角是__________
的___________三角形就是等边三角形.(相等,60度,等腰)
(10)直角三角形的性质:在直角三角形中,如果一个锐角等于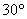 ,那么它所对的___________边等 ,那么它所对的___________边等
于__________的__________.(直角,斜边,一半)
二、方法思想
1.对称思想:利用轴对称可创造平衡、和谐、完美,是探索图形性质及发现图形关系的手段之一,利
用轴对称常可巧妙解决有关问题.
2.转化思想:解决轴对称问题、进行轴对称作图、设计图案等,都可转化为点与点之间的轴对称问
题.另外根据轴对称的性质可将“线段之和最小”的问题转化为两点之间的最短距离问题.
3.分类讨论思想:在涉及等腰三角形的边或角问题时,常常需分情况讨论,且根据三角形三边关系或
三角形内角和为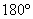 检验是否成立. 检验是否成立.
4.构造思想:添加辅助线构造线段垂直平分线性质的基本图形,构造等腰三角形或构造等腰三角形性
质的基本图形可巧妙解决有关问题.
三、考点解析
【轴对称】
1.轴对称图形的识别
 1.(1)下列四个图形中,不是轴对称图形的是( ). 1.(1)下列四个图形中,不是轴对称图形的是( ).
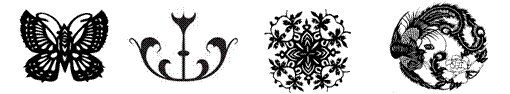
A. B. C. D.
答案:D
(2)下列图形是轴对称图形的是( ).

A. B. C. D.
答案:A
(3)请同学们写出两个具有轴对称性的汉字___________.
参考答案:羊,串
2.对称轴的考察
 2.(1)在下列对称图形中,对称轴的条数最少的图形是( ). 2.(1)在下列对称图形中,对称轴的条数最少的图形是( ).
A.圆 B.等边三角形 C.正方形 D.正六边形
答案:B
(2)易错点———角的对称轴是___________.
答案:角平分线所在直线
3.轴对称和轴对称图形的性质
共同的特征:对折后的两部分是完全重合的,即对应线段相等,对应角相等.
性质:(1)关于某条直线成轴对称的两个图形全等;
(2)对称轴是对应点所连线段的垂直平分线.
 3. 3.
(1)如图,△ABC与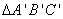 关于直线l对称,且∠A=98°,∠C`=28°,则∠B的度数为( ). 关于直线l对称,且∠A=98°,∠C`=28°,则∠B的度数为( ).
A.48° B.54° C.74° D.78°
(2)如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则
 ( ). ( ).
A.40° B.30° C.20° D.10°
(3)如图,等边△ABC的边长为1 cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点
A′处,且点在△ABC外部,则阴影部分图形的周长为___________cm.
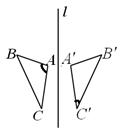 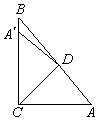 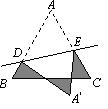
第(1)题图 第(2)题图 第(3)题图
答案: (1)B; (2)D; (3)3
4.利用轴对称设计图案
 4.在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示). 4.在学习“轴对称现象”内容时,王老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).

A B C
(1)小明的这三件文具中,可以看做是轴对称图形的是___________(填字母代号);
(2)请用这三个图形中的两个拼成一个轴对称图案,在答题卡的指定位置画出草图(只须画出一种);
答案:(1)B、C (2)略。
5.运用轴对称的性质解决几何问题
 5.(1)如图所示的矩形纸片,先沿虑线按箭头方向向右对折,接着将对折后的纸片沿虑线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个( ) 5.(1)如图所示的矩形纸片,先沿虑线按箭头方向向右对折,接着将对折后的纸片沿虑线剪下一个小圆和一个小三角形,然后将纸片打开是下列图中的哪一个( )
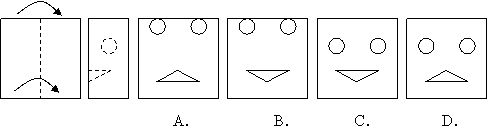
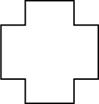
*(2)用一个正方形纸想剪出如图所示的图形,应先将纸怎样折叠,才能使剪的次数最少?
答案:(1)C
(2)解:如图,折叠三次后剪1刀。
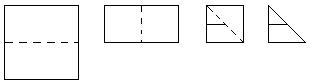
【线段垂直平分线】
线段的垂直平分线的知识是研究几何的基础,许多与之相关的问题,若能巧妙的运用线段垂直平分线的知识,既能省去一次三角形全等的证明,而且还使得求解过程更为简洁.
1.求图形的角度
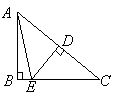  1.如图,在 1.如图,在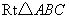 中, 中,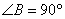 , , 是 是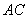 的垂直平分线,交 的垂直平分线,交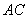 于点 于点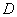 ,交 ,交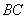 于点 于点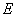 .已知 .已知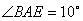 ,则 ,则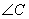 的度数为( ). 的度数为( ).
A.30° B.40° C.50° D.60°
答案:B
解析:∵ 是 是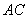 的垂直平分线,交 的垂直平分线,交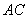 于点 于点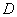 ,交 ,交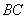 于点 于点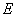 . .
∴AE=CE
∴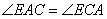
∵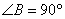 , ,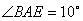
∴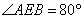
∴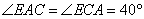
2.求线段的长度
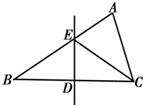  2.如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为 . 2.如图,在△ABC中,BC边上的垂直平分线DE交边BC于点D,交边AB于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为 .
答案:6
解析:∵BC边上的垂直平分线DE交边BC于点D,交边AB于点E
∴BE=CE,BD=CD
∵DE+EC+CD=24,即DE+BE+BD=24………①
又∵BD+BE-DE=12………②
由①-②得:2DE=12
∴DE=6
3.求图形周长
 3.如图,等腰△ABC的周长为21,底边BC = 5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( ). 3.如图,等腰△ABC的周长为21,底边BC = 5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( ).
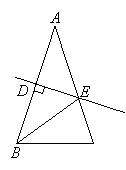
A.13 B.14 C.15 D.16
答案:A
*4.证明直线是线段的垂直平分线
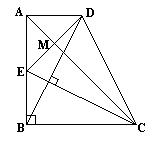  4.如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD. 4.如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
证明:(1)∵∠ABC=90°,BD⊥EC,
∴∠1与∠3互余,∠2与∠3互余,
∴∠1=∠2
∵∠ABC=∠DAB=90°,AB=BC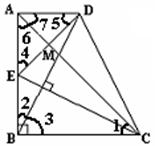
∴△BAD≌△CBE
∴AD=BE
(2)∵E是AB中点,
∴EB=EA
由(1)AD=BE得:AE=AD
∵AD∥BC
∴∠7=∠ACB=45°
∵∠6=45°
∴∠6=∠7
由等腰三角形的性质,得:EM=MD,AM⊥DE。
即AC是线段ED的垂直平分线。
(3)△DBC是等腰三角(CD=BD)
理由如下:
由(2)得:CD=CE
由(1)得:CE=BD
∴CD=BD
∴△DBC是等腰三角形。
5.运用线段垂直平分线的性质解决几何问题
 5.(1)如图所示,点A和点B关于某条直线成轴对称,你能作出这条直线吗? 5.(1)如图所示,点A和点B关于某条直线成轴对称,你能作出这条直线吗?

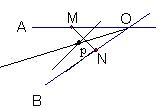
(2)如图,某地有两所大学和两条交叉的公路,点M、N表示大学,OA、OB表示公路,现计划修建一座物资仓库,希望仓库到两所大学的距离相同,到两条公路的距离也相同,你能确定出仓库应该建在什么位置吗?请在图中画出你的设计.
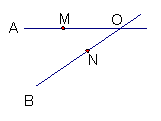
解:(1)如下图,连结AB,作线段AB的垂直平分线CD,则直线CD为所求。
(2)如下图,连结MN,作线段MN的垂直平分线,交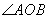 的平分线于点P,则点P即为所求。 的平分线于点P,则点P即为所求。
【轴对称变换】
由一个平面图形得到它的轴对称图形叫做轴对称变换.轴对称变换同旋转变换、平移变换一样,都是图形变换的一种,轴对称变换的实质就是图形的翻折,而翻折问题往往可以看作是图形的全等问题,解这类问题的关键是利用图形的全等,找出对应线段对应角,挖掘题目的隐含条件,再利用结论使问题获解.
注意:经过变换以后,只是位置发生了变化,图形的形状和大小并未改变.
1.作图
 1.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形. 1.如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
解:分别作出点A、B、C关于直线l的对称点A′、B′、C′,
作△A′B′C′,即为所求。

2.坐标系中的轴对称变换
点A(x1,y1)与B(x2,y2)关于x轴对称 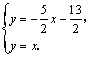
点A(x1,y1)与B(x2,y2)关于y轴对称 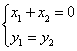
点A(x1,y1)与B(x2,y2)关于原点对称 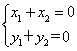
 2.(1)点P(3,-5)关于 2.(1)点P(3,-5)关于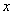 轴对称的点的坐标为( ) 轴对称的点的坐标为( )
A.(-3,-5) B.(5,3) C.(-3,5) D.(3,5)
(2)如图,在正方形网格纸上有一个△ABC
①作△ABC关于直线MN的对称图形;
②若网格上最小正方形边长为1,求△ABC的面积.
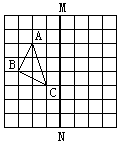
答案:(1)D; (2)①略 ②2.5
【综合运用】
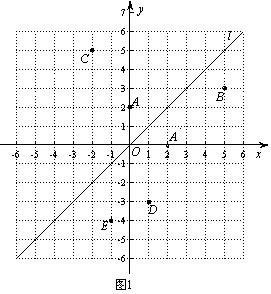
 1.(湖北省咸宁市)如图1,在平面直角坐标系中,直线l是第一、三象限的角平分线. 1.(湖北省咸宁市)如图1,在平面直角坐标系中,直线l是第一、三象限的角平分线.
实验与探究:
(1) 由图1观察易知A(0,2)关于直线l的对称点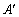 的坐标为(2,0),请在图中分别标明B(5,3) 、 的坐标为(2,0),请在图中分别标明B(5,3) 、
C(-2,5) 关于直线l的对称点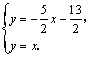 、 、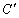 的位置,并写出他们的坐标: 的位置,并写出他们的坐标:
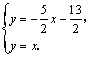 ___________、 ___________、  ____________; ____________;
归纳与发现:
(2) 结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平
分线l的对称点 的坐标为___________(不必证明); 的坐标为___________(不必证明);
运用与拓广:
(3) 已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求
出Q点坐标.
 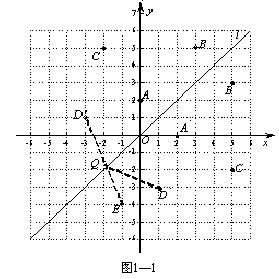
解:(1)如图1—1: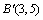 , ,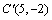
(2)(b,a)
(3)由(2)得,D(1,-3) 关于直线l的对称点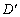 的坐标为(-3,1), 的坐标为(-3,1),
连接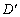 E交直线l于点Q,此时点Q到D、E两点的距离之和最小 E交直线l于点Q,此时点Q到D、E两点的距离之和最小 , ,
设过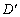 (-3,1) 、E(-1,-4)的设直线的解析式为 (-3,1) 、E(-1,-4)的设直线的解析式为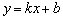 ,则 ,则
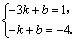 ∴ ∴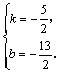
∴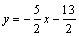 . .
由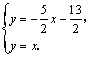 得 得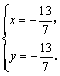
∴所求Q点的坐标为(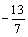 , ,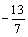 ) )
说明:由点E关于直线l的对称点也可完成求解.
|