|
一元二次方程的根的判别式
知识要点:
要点1.对于一元二次方程ax2+bx+c=0(a≠0)
当b2-4ac>0时,方程有两个不相等的实数根:

当b2-4ac=0时,方程有两个相等的实数根:
当b2-4ac<0时,方程没有实数根。
我们把b2-4ac叫做一元二次方程ax2+bx+c=0根的判别式,记作△=b2-4ac.
要点2.一元二次方程ax2+bx+c=0(a≠0) 有两个实数根x1、x2,则有

例题分析:
一、要点1的应用
 1. 不解方程,判定下列各方程根的情况 1. 不解方程,判定下列各方程根的情况
(1)2x2-6x-5=0;(2)2x2-12x+18=0; (3)3x2-5x+4=0; (4)x2-2x+k=0
解:(1)2x2-6x-5=0
∵a=2,b=-6,c=-5
∴△=b2-4ac=(-6)2-4×2×(-5)=36+40=76>0
∴2x2-6x-5=0有两个不相等的实数根
(2)2x2-12x+18=0,化简得:x2-6x+9=0
∵a=1,b=-6,c=9 ∴△=(-6)2-4×1×9=36-36=0
∴2x2-12x+18=0有两个相等的实数根
(3)3x2-5x+4=0
∵a=3,b=-5,c=4 ∴△=(-5)2-4×3×4=25-48=-23
∴3x2-5x+4=0没有实数根,即在实数范围内无解。
(4)x2-2x+k=0
∵a=1,b=-2,c=k ∴△=(-2)2-4×1×k=4(1-k)
∴当1-k>0时,即k<1时,△>0,方程x2-2x+k=0有两个不相等的实数根,
当1-k=0时,即k=1时,△=0,方程x2-2x+k=0有两个相等的实数根,
当1-k<0时,即k>1时,△<0,方程x2-2x+k=0无实根。
 2.已知:关于x的方程 2.已知:关于x的方程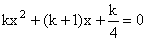 有两个不相等的实数根。 有两个不相等的实数根。
求k的取值范围。
解:∵关于x的方程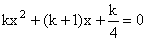 有两个不相等的实数根。 有两个不相等的实数根。
∴此方程中二次项的系数k≠0并且△>0
即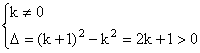
解得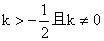
 3.已知:关于x的方程 3.已知:关于x的方程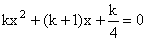 有实根,求k的取值范围。 有实根,求k的取值范围。
分析:当k≠0时,该方程是关于x的二次方程,它有实根,则△≥0;
当k=0时,原方程化为x的一元一次方程。
解: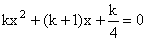
(1)当k=0时,原方程化为x=0;
(2)当k≠0时,△=(k+1)2-k2=2k+1≥0
解得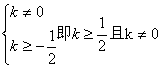
由(1)、(2),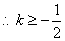
二、要点2的应用
 4.已知关于x的方程 kx2-2 (k+1) x+k-1=0 有两个不相等的实数根, 4.已知关于x的方程 kx2-2 (k+1) x+k-1=0 有两个不相等的实数根,
(1) 求k的取值范围;
(2) 是否存在实数k,使此方程的两个实数根的倒数和等于0 ?
若存在,求出k的值;若不存在,说明理由.
解: (1) ∵方程有两个不相等的实数根,
∴Δ=[-2(k+1)]2-4k(k-1)>0,且k≠0,解得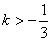 ,且k≠0 . ,且k≠0 .
即k的取值范围是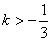 ,且k≠0 . ,且k≠0 .
(2) 假设存在实数k,使得方程的两个实数根x1 , x2的倒数和为0.
则x1 ,x2不为0,且 ,即 ,即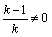 ,且 ,且 ,解得k=-1 . ,解得k=-1 .
而k=-1 与方程有两个不相等实根的条件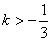 ,且k≠0矛盾, ,且k≠0矛盾,
故使方程的两个实数根的倒数和为0的实数k不存在.
 5.关于x的方程x2-(2k+1)x+k2=0。 5.关于x的方程x2-(2k+1)x+k2=0。
(1) 如果方程有实数根,求k的取值范围。
(2)设x1、x2是方程的两根,且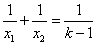 ,求k的值。 ,求k的值。
解:(1) ∵方程有实数根 ∴△≥0 即 [(2k+1)]2-4k2≥0
4k2+4k+1-4k2≥0 ∴4k+1≥0 ∴k≥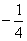
(2) 解:∵x、x2是方程的两根 ∴x1+x2=2k+1,x1·x2=k2
∵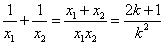 又∵ 又∵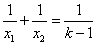 ∴ ∴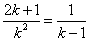
∴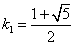 , ,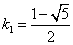 又∵k≥ 又∵k≥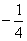 ∴ ∴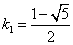 应舍去,k= 应舍去,k=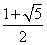
三、综合要点1,2的应用
 6.已知: x1、x2是关于x的方程x2+(2a-1)x+a2=0的两个实数根,且(x1+2)(x2+2)=11,求a的值。 6.已知: x1、x2是关于x的方程x2+(2a-1)x+a2=0的两个实数根,且(x1+2)(x2+2)=11,求a的值。
解:∵x1、x2是方程x2+(2a-1)x+a2=0的两个实数根,
∴x1+x2=1-2a,x1﹒x2=a2
∵(x1+2)(x2+2)=11, ∴x1x2+2(x1+x2)+4=11
∴a2+2(1-2a)-7=0,即a2-4a-5=0。
解得a=-1,或a=5。
又∵Δ=(2a-1)2-4a2=1-4a≥0,
∴a≤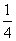 。 ∴a=5不合题意,舍去。 。 ∴a=5不合题意,舍去。
∴a=-1
 7.已知:关于x的一元二次方程x2+2(2-m)x+3-6m=0 7.已知:关于x的一元二次方程x2+2(2-m)x+3-6m=0
求证:无论m取什么实数,方程总有实数根。
证明:∵△=[2(2-m)]2-4(3-6m)=4[(2-m)2-(3-6m)]
=4(m2-4m+4-3+6m) =4(m2+2m+1)
=4(m+1)2≥0
∴无论m取什么实数,方程总有实数根。
 8.已知:a、b、c为实数, 8.已知:a、b、c为实数,
求证:关于x的一元二次方程(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0恒有实数根。
证明:原方程化为:3x2-2(a+b+c)x+(ab+bc+ca)=0
∴△=[-2(a+b+c)]2-12(ab+bc+ca)
=4(a2+b2+c2-ab-bc-ca)
=2[(a2-2ab+b2)+(b2-2bc+c2)+(c2-2ca+a2)]
=2[(a-b)2+(b-c)2+(c-a)2]
∵a、b、c为实数
∴(a-b)2≥0,(b-c)2≥0,(c-a)2≥0
∴△≥0
∴原方程恒有实数根。
 9.求函数 9.求函数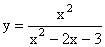 中y的取值范围。 中y的取值范围。
解: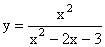
∴y(x2-2x-3)=x2
∴(y-1)x2-2yx-3y=0
(1)当y=1时,方程化为2x+3=0,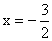
(2)当y≠1时,
△=4y2+12y(y-1)=4y(4y-3)≥0
即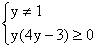 解得y≤0或 解得y≤0或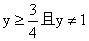
由(1)、(2),∴y的取值范围是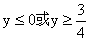 . .
|