|
八年级第二学期数学期末复习――代数部分
一.复习范围及知识要点:
1.分式方程的应用:
会列分式方程解应用问题。对于分式方程的考查,难度应控制在课本的范围内。
2.反比例函数:
反比例函数的概念,反比例函数的图象和性质,用反比例函数知识解决现实生活中的实际问题;能用反比例函数解决某些实际问题。
正确理解反比例函数概念是基础,结合图像掌握其性质是重点,利用反比例函数解决实际问题是难点。
3.数据的分析:
会计算一组数据的平均数(主要是加权平均数),中位数,众数以及极差,方差;
能通过对数据的分析 ,作出合理的判断,认识统计对决策的作用,能比较清晰地表达自己的观点。根据统计图、表,通过计算分析解决实际问题.
4.二次根式:
了解二次根式的概念,会确定二次根式有意义的条件,了解最简二次根式的概念,会利用二次根式的性质进行化简,理解二次根式的加、减、乘、除运算的运算法则,会进行二次根式的混合运算;二次根式在几何问题中的应用。
5.一元二次方程的解法:
一元二次方程的一般形式及其解法;会准确熟练的求解一元二次方程。
二、具体复习建议
1.夯实基础,狠抓落实
弄清主要的一些概念、定理有哪些?内容是什么?因、果关系是什么;
整理所学知识,形成知识网络及方法系统;
对各部分知识的难、易,以及自己的学情要有基本的认识,了解易错点,抓住易错点,通过练习,不断纠正、巩固;
2.应制定好整体的复习安排,循序渐进
对重要内容,但是有一定难度的知识及思想方法,要贯穿在整个复习之中,以期提升复习效果。
3.复习例题及习题的选用应有明确的目的
精选例题及习题,例题的选择,要明确针对易出现的错误类型,使知识的复习达到再现和纠错的目的,对再次出现的问题应重复训练巩固。
三.例题分析:
 1.甲、乙两艘旅游客轮同时从台湾省某港出发来厦门。甲沿直航线航行180海里到达厦门;乙沿原来航线绕道香港后来厦门,共航行了720海里,结果乙比甲晚20小时到达厦门。已知乙速比甲速每小时快6海里,求甲客轮的速度(其中两客轮速度都大于16海里/小时)? 1.甲、乙两艘旅游客轮同时从台湾省某港出发来厦门。甲沿直航线航行180海里到达厦门;乙沿原来航线绕道香港后来厦门,共航行了720海里,结果乙比甲晚20小时到达厦门。已知乙速比甲速每小时快6海里,求甲客轮的速度(其中两客轮速度都大于16海里/小时)?
解:设甲客轮速度为每小时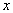 海里,根据题意得: 海里,根据题意得:
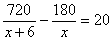
整理,得: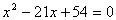 解得: 解得: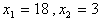
经检验,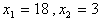 都是所列方程的解。 都是所列方程的解。
但速度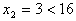 不合题意,所以只取 不合题意,所以只取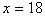 。 。
答:甲客轮的速度为每小时18海里。
 2.“丽园”开发公司生产的960件新产品,需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元。 2.“丽园”开发公司生产的960件新产品,需要精加工后,才能投放市场。现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天,而乙工厂每天比甲工厂多加工8件产品,公司需付甲工厂加工费用每天80元,乙工厂加工费用每天120元。
(1)求甲、乙两个工厂每天各能加工多少件新产品。
(2)公司制定产品加工方案如下:可以由每个厂家单独完成;也可以由两个厂家同时合作完成。在加
工过程中,公司需派一名工程师每天到厂进行技术指导,并负担每天5元的误餐补助费。
请你帮助公司选择一种既省时又省钱的加工方案,并说明理由。
解:(1)设甲工厂每天能加工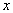 件产品, 件产品,
则乙工厂每天能加工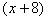 件产品。 件产品。
根据题意,得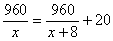
整理,得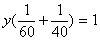
解得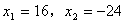 。 。
经检验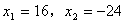 都是原方程的根。但是每天能加工的产品数不能为负数, 都是原方程的根。但是每天能加工的产品数不能为负数,
所以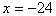 舍去,只取 舍去,只取 。 。
当 时, 时,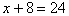 。 。
答:甲、乙两个工厂每天各能加工16件和24件新产品。
(2)甲工厂单独加工完这批新产品所需的时间为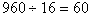 (天), (天),
所需要费用为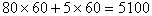 (元)。 (元)。
乙工厂单独加工完这批新产品所需的时间为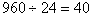 (天), (天),
所需费用为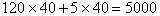 (元); (元);
设他们合作完成这批新产品所用的时间为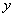 天,于是 天,于是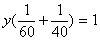 , ,
解得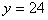 (天),所需费用为 (天),所需费用为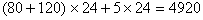 (元)。 (元)。
因为甲、乙两家工厂合作所用时间和钱数都最少,
所以选择甲、乙两家工厂合作加工完这批新产品比较合适。
 3.已知:反比例函数 3.已知:反比例函数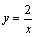 和 和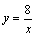 在平面直角坐标系xOy第一象限中的图象如图1所示,点A在 在平面直角坐标系xOy第一象限中的图象如图1所示,点A在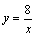 的图象上,AB∥y轴,与 的图象上,AB∥y轴,与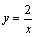 的图象交于点B,AC、BD与x轴平行,分别与 的图象交于点B,AC、BD与x轴平行,分别与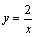 、 、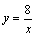 的图象交于点C、D. 的图象交于点C、D.
(1)若点A的横坐标为2,求梯形ACBD的对角线的交点F的坐标;
(2)若点A的横坐标为m,比较△OBC与△ABC的面积的大小,并说明理由;
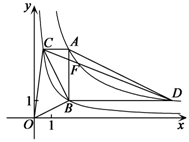
图1
解:(1)如图2,当点A的横坐标为2时,点A、B、C、D的坐标分别为 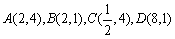 . .
直线CD的解析式为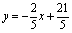 . .
∵ AB∥y轴,F为梯形ACBD的对角线的交点,
∴ x=2时,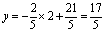 . .
∴ 点F的坐标为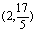 . .
(2)如图3,作BM⊥x轴于点M.作CN⊥x轴于点N.当点A的横坐标为m时,
点A、B、C、D的坐标分别为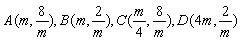 . .
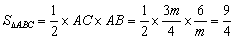 . .
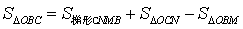
 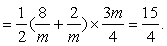
∴ 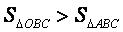 . .
 
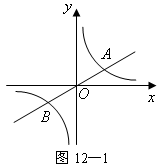
 4.如图12—1已知直线 4.如图12—1已知直线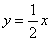 与双曲线 与双曲线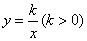 交于 交于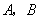 两点,且点 两点,且点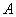 的横坐标为 的横坐标为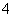 . .
(1)求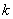 的值; 的值;
(2)若双曲线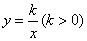 上一点 上一点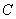 的纵坐标为8,求 的纵坐标为8,求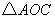 的面积; 的面积;
(3)过原点 的另一条直线 的另一条直线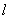 交双曲线 交双曲线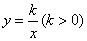 于 于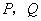 两点( 两点(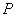 点在第一象限),若由点 点在第一象限),若由点
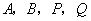 为顶点组成的四边形面积为 为顶点组成的四边形面积为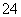 ,求点 ,求点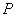 的坐标. 的坐标.
解:(1)∵点A横坐标为4 , ∴当 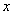 = 4时, = 4时,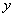 = 2 . = 2 .
∴ 点A的坐标为( 4,2 ).
∵ 点A是直线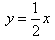 与双曲线 与双曲线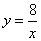 (k>0)的交点 , (k>0)的交点 ,
∴ k = 4 ×2 = 8 .
(2)如图12—2,
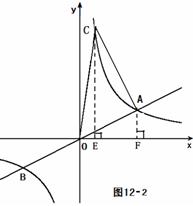 过点 C、A分别做 过点 C、A分别做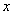 轴的垂线,垂足为E、F, 轴的垂线,垂足为E、F,
∵ 点C在双曲线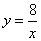 上,当 上,当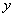 = 8时, = 8时,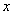 = 1 . = 1 .
∴ 点C的坐标为 ( 1, 8 ).
∵ 点C、A都在双曲线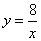 上 , 上 ,
∴ S△COE =S△AOF =4 。
∴ S△COE +S梯形CEFA = S△COA + S△AOF .
∴ S△COA =S梯形CEFA .
∵ S梯形CEFA = 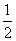 ×(2+8)×3 = 15 , ×(2+8)×3 = 15 ,
∴ S△COA = 15 .
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
∴ OP=OQ,OA=OB .
 ∴ 四边形APBQ是平行四边形 . ∴ 四边形APBQ是平行四边形 .
∴ S△POA = 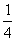 S平行四边形APBQ = S平行四边形APBQ = 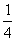 ×24 = 6 . ×24 = 6 .
设点P的横坐标为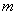 ( (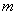 > 0且 > 0且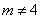 ), ),
得P ( 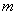 , ,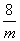 ) . ) .
过点P、A分别做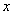 轴的垂线,垂足为E、F, 轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4 .
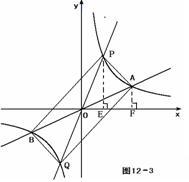
若0<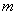 <4,如图12-3, <4,如图12-3,
 ∵ S△POE + S梯形PEFA = S△POA + S△AOF, ∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6 .
∴ 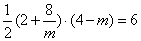 . .
解得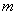 = 2, = 2,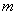 = - 8(舍去) . = - 8(舍去) .
∴ P(2,4).
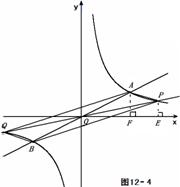
若 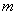 > 4,如图12-4, > 4,如图12-4,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∴ S梯形PEFA = S△POA = 6 .
∴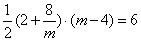 , ,
解得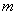 = 8, = 8,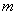 = - 2 (舍去) . = - 2 (舍去) .
∴ P(8,1).
∴ 点P的坐标是P(2,4)或P(8,1).
 5.国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图5所示,其中分组情况是: 5.国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图5所示,其中分组情况是:
A组: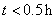 ; B组: ; B组: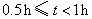 ; ;
C组: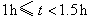 ;D组: ;D组: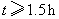 ; ;
请根据上述信息解答下列问题:
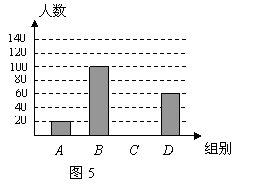
(1)C组的人数是______________;
(2)本次调查数据的中位数落在______________组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
解:(1)120;
(2)C;
(3)达国家规定体育活动时间的人数约占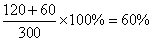 . .
所以,达国家规定体育活动时间的人约有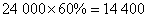 (人). (人).
|