|
等腰三角形(一)(概念、性质及判定)
教学目标:
掌握等腰三角形的有关概念和相关性质及判定;熟练运用等腰三角形的性质及判定解决一些证明和等腰三角形边角的计算问题。
教学内容解析:
一、知识要点:
定义:有两条边相等的三角形叫做等腰三角形.
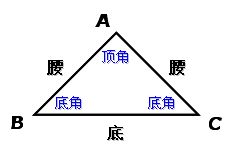
相关概念:
边:等腰三角形中,相等的两条边叫做腰,另一条边叫做底边.
角:等腰三角形中,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
对称性:等腰三角形是轴对称图形,对称轴是底边上的高(或底边上的中线或顶角的平分线)所在的直线.
性质:
1.等腰三角形,底边上的高,底边上的中线和顶角的平分线三线合一;
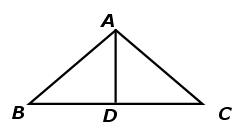
如图,在△ABC中,AB =AC, 点 D在BC上
(1)如果∠BAD =∠CAD ,那么AD⊥BC,BD=CD
(2)如果 BD=CD,那么∠BAD =∠CAD,AD⊥BC
(3)如果 AD⊥BC,那么∠BAD =∠CAD,BD=CD
(为了方便记忆可以说成“知一求二”)
2.等腰三角形中相等的边所对的角也相等.
判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
(为了方便记忆可以简称为:“等边对等角”和“等角对等边”)
二、典型例题:
例一:
1、在等腰△ABC中,AB =3,AC = 4,则 △ABC的周长=________
2、在等腰△ABC中,AB =3,AC = 7,则 △ABC的周长=________
分析:此例题的重点是运用等腰三角形的定义,以及等腰三角形腰和底边的关系,仔细比较以上两个例题,并强调在没有明确腰和底边之前,应该分两种情况讨论。而且在讨论后还应该思考一个问题,就是这样的三条边能否构成三角形。
答案:1、10或11;2、17。
例二:
1、在等腰△ABC中,AB =AC, ∠A = 50°, 则∠B =_____,∠C=______
2、在等腰△ABC中,∠A =100°, 则∠B =______,∠C=______
分析:此例题的重点是运用等腰三角形“等边对等角”这一性质,突出顶角和底角的关系,强调等腰三角形中顶角和底角的取值范围:0°<顶角<180°, 0°<底角<90°。仔细比较以上两个例题,得出一个结论:在等腰三角形中,已知一个角就可以求出另外两个角。
答案:1、65°,65°;2、40°,40°。
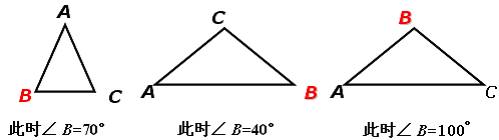
例三:在等腰△ABC中,∠A = 40°, 则∠B =______
分析:此题是一道陷阱题,可以先进行分析,和例二的2小题比较,估计会出一些状况,大多数学生会按照两种情况讨论,得到两个答案。画出图形进行分析,分两种情况讨论,但是答案是“三个”。强调需要自己画图解题时,一定要三思而后行!
答案:
例四:在△ABC中,AB =AC,点D是BC的中点,∠B = 40°,求∠BAD的度数?
分析:此题的目的在于等腰三角形“等边对等角”和“三线合一”性质的综合运用,以及怎么书写解答题,强调“三线合一”的表达过程。

解:在△ABC中,
∵AB = AC,∠B =40°,∴∠B=∠C =40°
又∵∠BAC +∠B +∠C =180°, ∴∠BAC =100°
在△ABC中,AB = AC,点D是BC的中点,
∴AD是底边上的中线
根据等腰三角形“三线合一”知:
AD是∠BAC的平分线 ,即∠BAD =∠CAD = 50°
例五:如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°。
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们
认为木桩是垂直横梁的。
请同学们想想,工人师傅的说法对吗?请说明理由。
 
分析:此题的目的在于把实际问题转化为等腰三角形“等边对等角”和“三线合一”性质的综合运用。
解:① 
据等边对等角得: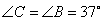
②  ,又 ,又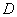 为 为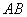 的中点 的中点
据三线合一得: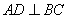
综上可得,工人师傅的说法是对的。
例六:已知:如图,在△ABC中,AB=AC,E在AC上,D在BA的延长线上,AD=AE,连结DE。请问:DE⊥BC成立吗?
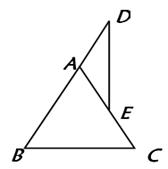 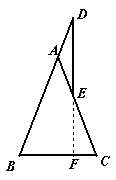 
解法一:延长DE交BC于F
由等边对等角可得∠B=∠C,∠D=∠AED,
又∠BAC=∠D+∠AED,∠FEC=∠AED=∠D
又∵∠B+∠C+∠BAC=180°
∴2∠C+∠D+∠AED=180°,
即2∠C+2∠FEC=180°
等式两边同除以2,得∠C+∠FEC=90°,命题得证。
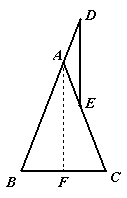
解法二:过A作AF⊥BC于F
由等边对等角可得∠D=∠AED,
由等腰三角形三线合一可得AF平分∠BAC
又∠BAC=∠D+∠AED=2∠D,
∴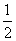 ∠BAC=∠D,即∠BAF=∠D ∠BAC=∠D,即∠BAF=∠D
∴ 可得AF∥DE,又∵AF⊥BC
∴DE⊥BC, 命题得证。
例七:如图,△ABC中,AB=AC,∠ABC与∠ACB的平分线交于F,过F作DE∥BC交AB于D,交AC于E.
(1)找出图中的等腰三角形;
(2)BD、CE之间存在着什么样的关系?证明你的发现.
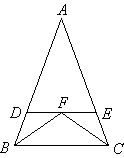
答案:(1)△ABC,△ADE,△DBF,△EFC,△FBC。
(2)BD=CE(等量减等量差相等)
例八:

例九:
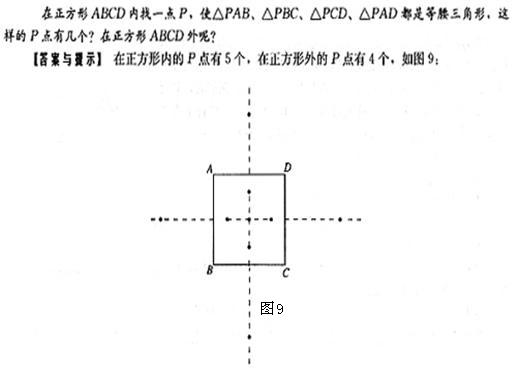
例十:
已知AB是一个等腰三角形的一边,其另一个顶点C的集合是什么?
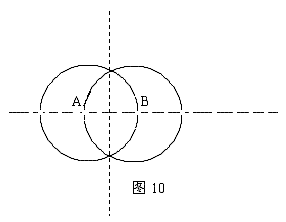
【答案与提示】:如图10,点C的集合是分别以A,B为圆心,AB长为半径的两圆(不含直线AB与圆的交点)以及线段AB的垂直平分线(不含AB的中点)。
|