| 名称 |
定义 |
性质 |
判定 |
面积 |
平
行
四
边
形 |
两组对边分别平行的四边形叫做平行四边形。 |
①对边平行;
②对边相等;
③对角相等;
④邻角互补;
⑤对角线互相平分;⑥是中心对称图形 |
①定义;
②两组对边分别相等的四
边形;
③一组对边平行且相等的
四边形;
④两组对角分别相等的四
边形;
⑤对角线互相平分的四边
形。 |
S=ah(a为一边长,h为这条边上的高) |
矩
形 |
有一个角是直角的平行四边形叫做矩形 |
除具有平行四边形的性质外,还有:①四个角都是直角;②对角线相等;③既是中心对称图形又是轴对称图形。 |
①有三个角是直角的四边形是矩形;②对角线相等的平行四边形是矩形;③定义。 |
S=ab(a为一边长,b为另一边长) |
菱
形 |
有一组邻边相等的平行四边形叫做菱形。 |
除具有平行四边形的性质外,还有①四条边相等;②对角线互相垂直,且每一条对角线平分一组对角;③既是中心对称图形又是轴对称图形。 |
①四条边相等的四边形是菱形;②对角线垂直的平行四边形是菱形;③定义。 |
①S=ah(a为一边长,h为这条边上的高);
②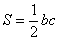 (b、c为两条对角线的长) (b、c为两条对角线的长) |
正
方
形 |
有一组邻边相等且有一个角是直角的平行四边形叫做正方形 |
具有平行四边形、矩形、菱形的性质:①四个角是直角,四条边相等;②对角线相等,互相垂直平分,每一条对角线平分一组对角;③既是中心对称图形又是轴对称图形。 |
①有一组邻边相等的矩形是正方形;②有一个角是直角的菱形是正方形;③定义。 |
①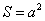 (a为边长); (a为边长);
②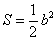 (b为对角线长) (b为对角线长) |