|
四边形复习
【教学目标】
探索并掌握平行四边形,矩形,菱形,正方形,等腰梯形的意义,性质,判定方法,四边形的学习要善于采用“类比”的方法,从“一般到特殊”的认识规律。
【典型例题】
 1、在□ABCD中,∠A的平分线分BC成4cm 和3cm两部分,则□ABCD的周长为____________. 1、在□ABCD中,∠A的平分线分BC成4cm 和3cm两部分,则□ABCD的周长为____________.
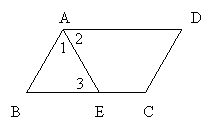
【考查内容】平行四边形的性质.
解:∵AE平分∠BAD,∴∠1=∠2.
∵在□ABCD中,AD//BC
∴∠2=∠3.
∴∠1=∠3,∴AB=BE
(1)当BE=4cm时,AB=4cm,CE=3cm,∴□ABCD的周长为22cm;
(2)当BE=3cm时,AB=3cm,CE=4cm,∴□ABCD的周长为20cm;
综上所述,□ABCD的周长为20cm或22cm.
 2、已知,如图,△ABC中,D为AB的中点,E是AC上的一点,EF//BD,DF//BE,则 2、已知,如图,△ABC中,D为AB的中点,E是AC上的一点,EF//BD,DF//BE,则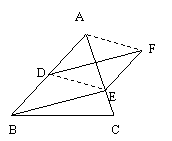 DF与AE间的关系 DF与AE间的关系
是____________.
【考查内容】平行四边形的性质与判定.
解:连结AF、DE
∵EF//BD,DF//BE
∴四边形BDFE为平行四边形.
∴EF=BD
∵D为AB的中点,∴AD=BD
∴EF=AD
∵EF//AD
∴四边形ADEF为平行四边形.
∴DF与AE互相平分.
 3、如图,在 3、如图,在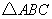 中, 中,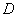 是 是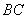 边上的一点, 边上的一点, 是 是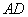 的中点,过点 的中点,过点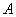 作 作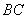 的平行线交 的平行线交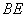 的延长线于 的延长线于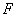 ,且 ,且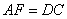 ,连接 ,连接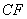 . .
(1)求证: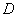 是 是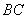 的中点; 的中点;
(2)如果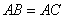 ,试猜测四边形 ,试猜测四边形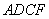 的形状,并证明你的结论. 的形状,并证明你的结论.
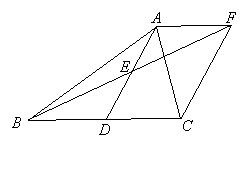
【考查内容】矩形的判定
解:(1)∵E为AD的中点,∴AE=DE.
∵AF//BD,∴∠AFE=∠EBD.
又∵∠AEF=∠BED
∴△AEF≌△DEB(AAS)
∴AF=BD
∵AF=CD,∴BD=CD
∴点D为BC的中点.
(2)∵AF//BC,AF=CD,∴四边形ADCF是平行四边形.
∵AB=AC,点D为BC的中点,∴AD⊥BC,即∠ADC=90°.
∴□ADCF为矩形.
 4、如图,已知□ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,求该平行四边形的面积. 4、如图,已知□ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,求该平行四边形的面积.
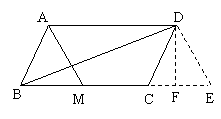
【考查内容】平行四边形的面积的求法。
解:过点D作DE//AM,交BC延长线于点E,
过点D作DF⊥BE于F.
∵在□ABCD中,AD//BC,∴四边形ADEM为平行四边形.
∴DE=AM=9,EM=AD=10.
∵M为BC的中点,∴BM=5,∴BE=15
∵BD2+DE2=BE2,∴∠BDE=90°.
∴BD·DE=BE·DF,即12×9=15·DF,∴DF= . .
∴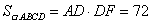 . .
 5、如图,在梯形ABCD中,AD//BC, 5、如图,在梯形ABCD中,AD//BC,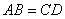 .若AC⊥BD,AD+BC= .若AC⊥BD,AD+BC=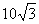 , 且 , 且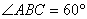 , 求CD的长. , 求CD的长.
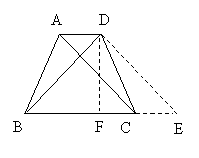
【考查内容】梯形中常见的辅助线的添加。
解:过点D作DE//AC,交BC延长线于点E,
过点D作DF⊥BC于F
∵AD//BC,∴四边形ADEC为平行四边形.∴CE=AD,DE//AC,DE=AC.
∴BE=BC+CE=BC+AD=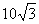 . .
∵在梯形ABCD中,AD//BC,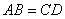 ,AC⊥BD, ,AC⊥BD,
∴AC=BD,DE⊥BD,DE=BD
∴△BDE为等腰直角三角形,∴DF=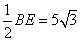 . .
∵∠DCB=∠ABC=60°,∴CD=10.
 6、如图,已知BD、CE是△ABC的两条高,M、N分别是BC、DE的中点. 6、如图,已知BD、CE是△ABC的两条高,M、N分别是BC、DE的中点.
求证:(1)EM=DM;(2)MN⊥DE.

【考查内容】直角三角形的斜边中线等于斜边的一半。
证明:∵BD、CE是△ABC的两条高
∴∠BDC=∠BEC=90°
∵在Rt△BDC中,M为BC的中点,
∴DM=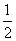 BC. BC.
同理可得,EM=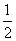 BC BC
∴DM=EM
∵点N是DE的中点,∴MN⊥DE.
 7、如图,折叠矩形纸片ABCD,先折出折痕(对角线)BD,在折叠使AD边与对角线BD重合,得折线DG, 若AB=2, BC=1, 求AG. 7、如图,折叠矩形纸片ABCD,先折出折痕(对角线)BD,在折叠使AD边与对角线BD重合,得折线DG, 若AB=2, BC=1, 求AG.

【考查内容】矩形中折叠问题,关注折叠前后的对应边和对应角。
解:设AG=x,
由题意得,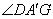 =90°,BG=2- x, =90°,BG=2- x,
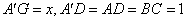 , ,
∵AD=1,AB=2,∴BD=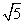 ∴ ∴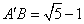 . .
∵在Rt△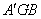 中, 中,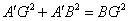 ,即 ,即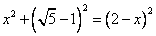 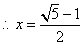
∴AG=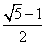 . .
 8、如图1,在 8、如图1,在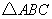 中, 中,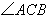 为锐角,点 为锐角,点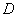 为射线 为射线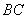 上一点,连结 上一点,连结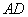 ,以 ,以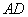 为一边且在 为一边且在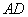 的右侧作正方形 的右侧作正方形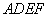 . .
(1)如果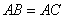 , ,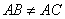 , ,
①当点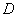 在线段 在线段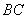 上时(与点 上时(与点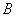 不重合),如图2,线段 不重合),如图2,线段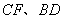 所在直线的位置关系 所在直线的位置关系
为 __________ ,线段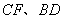 的数量关系为____________; 的数量关系为____________;
②当点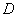 在线段 在线段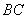 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由; 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
  
(2)如果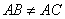 , ,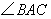 是锐角,点 是锐角,点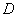 在线段 在线段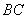 上,当 上,当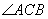 满足什么条件时, 满足什么条件时,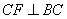
(点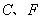 不重合),并说明理由. 不重合),并说明理由.
解:(1)①CF⊥BD,CF=BD;
②成立,理由如下:
∵在正方形ADEF中,AD=AF,∠DAF=90°,
∴∠BAD+∠CAD =90°,∠CAF+∠CAD =90°
∴∠BAD=∠CAF
∵AB=AC,∴△BAD≌△CAF(SAS)
∴BD=CF,∠ABD=∠ACF=45°.
∴∠BCF=∠BCA+∠ACF=90°.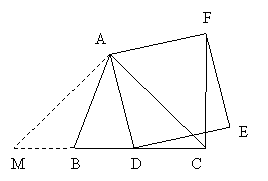
(2) 当∠ACB=45°时,CF⊥BD,理由如下:
过点A作AM⊥AC,交CB延长线于点M,
则△AMC为等腰直角三角形,
同上易证△AMD≌ACF(SAS)
∴∠AMD=∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°,
∴CF⊥BD.
练习:
1. 在□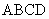 中,∠C=60°,DE⊥AB于E,DF⊥BC于F. 中,∠C=60°,DE⊥AB于E,DF⊥BC于F.
(1)则∠EDF=___________;
(2)如图,若AE=4,CF=7,则□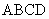 周长=____________. 周长=____________.
2.如图,在 ABC中,EF为 ABC中,EF为 ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连接DE、DF,要使四边形AEDF为平行四边形,需要添加条件______________.(只添加一个条件) ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连接DE、DF,要使四边形AEDF为平行四边形,需要添加条件______________.(只添加一个条件)
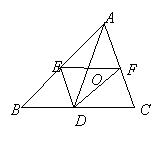
3. 如图,四边形ABED和四边形AFCD都是平行四边形,AF和DE相交成直角,AG=3cm,DG=4cm,□ABED的面积是36cm2,则四边形ABCD的周长为____________.
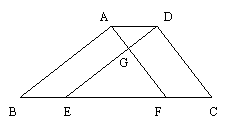
4. 如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E.
(1)求证:梯形ABCD是等腰梯形.
(2)若∠BDC=30°,AD=5,求CD的长.
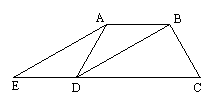
5. 如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在D’处,求重叠部分△AFC的面积。
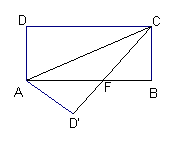
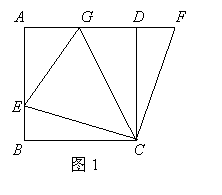
6. 如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
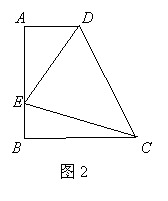
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,
E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
参考答案:
1、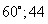
2、点D为BC的中点
3、46cm
4、(1)略(2)10
5、10
6、(1)提示:可证出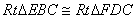 (2)成立; (3)10 (2)成立; (3)10
|