|
周末练习9(梯形同步练习)
一、选择题(每题3分,共18分)
1.在等边三角形、平行四边形、矩形、菱形和等腰梯形中,既是轴对称图形又是中心对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.在等腰梯形ABCD中,AB∥CD,∠D=2∠A,AB-CD=8,则AD=( )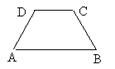
A.6 B.7 C.8 D.9
3.下列说法正确的是( )
A.平行四边形是一种特殊的梯形 B.等腰梯形的同一底上的两底角相等
C.有两邻角相等的梯形是等腰梯形 D.过梯形上、下底中点的直线是梯形的对称轴
4.在梯形中,①两腰相等;②两底平行;③对角线相等;④两底相等。正确的有( )
A.1个 B.2个 C.3个 D.4个
5.等腰梯形的上底与高相等,下底是上底的3倍,则下底角的度数是( )
A.30° B.45° C.45°和135° D.60°
6.等腰梯形两底之差等于一腰长,它与下底的夹角是( )
A.15° B.30° C.45° D.60°
二、填空题(每题4分,共40分)
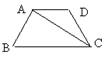
1.如图,梯形ABCD中,AD∥BC,AB=CD,∠B=60°,AC⊥AB,那么∠ACD=_____°,∠D=_____°
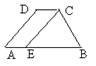
2.如图,梯形ABCD中,AB∥CD,CE∥AD,△CEB的周长为15,AE=4,则梯形的周长为___________
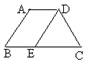
3.如图,梯形ABCD中,BC∥AD,DE∥AB,DE=DC,∠A=100°,则∠B=____________°,
∠C=____________°,∠ADC=____________°,∠EDC=____________ °
4.等腰梯形的上、下底长分别为6cm和8cm,且有一个角是60°,则它的腰长为____________
5.已知梯形的上、下底长分别为6、8,一条腰长为7,则另一条腰长a的取值范围是_________,若这条
腰长为奇数,则此梯形为____________梯形。
6.如果等腰梯形两底之差等于一腰长,那么这个等腰梯形的底角的度数是____________°
7.若等腰梯形一腰上的两个内角的度数之比为1∶3。则它的各个内角的度数分别是___________
8.已知梯形ABCD中,AD∥BC,AB=CD,∠C=60°,AD=3cm,DC=5cm,那么梯形ABCD的周长是_____
9.已知梯形ABCD中,AD∥BC,AB=CD=6cm,AD=4cm,BC=10cm,则∠A=____________°
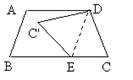
10.如图,等腰梯形ABCD中,AD∥BC,∠ABC=72°,平移腰AB到DE,再将△DCE沿DE翻折,得到
△DC’E,则∠EDC’ =____________
三、解答题(每题15分,共30分)
1.如图,AD∥BC,AB=CD,BD平分∠ABC,∠ADB=30°,AD=3cm,
求梯形ABCD的周长。
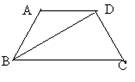
2.如图,AD∥BC,∠DBC=∠ACB=30°,∠ADC=2∠DCB
⑴求∠ADC和∠DCB的度数;⑵求∠BDC和∠DCA的度数。
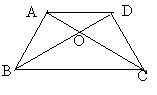
四、(12分)
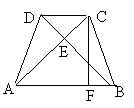
如图,梯形ABCD中,AB∥CD,AD=BC,AC⊥BD于E,CF是梯形的高,
试说明CF=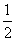 (AB+CD), (AB+CD),
梯形同步练习参考答案
一、1.B
2.C
3.B
4.A
5.B
6.D
二、1.30°、120°
2.23
3.80°、80°、100°、20°
4.2cm
5.5<a<9 等腰
6.60°或120°
7.45°、135°、135°、45°
8.21cm
9.120°
10.36°
三、
1.∵AD∥BC ∴∠DBC=∠ADB=30°(两直线平行,内错角相等)
∵BD平分∠ABC ∴∠ABD=∠DBC=30° ∴∠ADB=∠ABD ∴AB=AD=3cm(等角对等边)
∵梯形ABCD中,AD∥BC,AB=CD,∴∠C=∠ABC=60°(等腰梯形同一底上的两角相等)
∴△BDC中,∠BDC=180°-∠C-∠DBC=90°,
∵∠DBC=30°∴BC=2CD=6cm(直角三角形中,30°的锐角所对的直角边等于斜边的一半)
∴梯形ABCD的周长=15
2.∵AD∥BC ∴∠ADC+∠DCB=180°(两直线平行,同旁内角互补)
∵∠ADC=2∠DCB ∴∠ADC=120°,∠DCB=60°
∴△BCD中,∠BDC=180°-∠DCB-∠DBC=180°-60°-30°=90°
∠DCA=∠DCB-∠ACB=60°-30°=30°
四、
解:过C作CG∥DB交AB的延长线于G,∵BG∥CD,CG∥BD
∴四边形BGCD是平行四边形(两组对边分别平行的四边形是平行四边形)
∴BG=CD,CG=BD(平行四边形的对边相等)
∴AB+CD=AB+BG=AG
∵梯形ABCD中,AB∥CD,AD=BC
∴AC=BD(等腰梯形的对角线相等)∴AC=CG
又∵CF⊥AB ∴CF是AG边上的中线(等腰三角形的“三线合一”)
∵CG∥BD ∴∠ACG=∠AEB=90°
∴CF=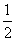 AG(直角三角形斜边上的中线等于斜边的一半) AG(直角三角形斜边上的中线等于斜边的一半)
即CF=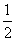 (AB+CD) (AB+CD)
|