|
分式的运算及分式方程
教学目标:
1、会进行简单的分式加、减、乘、除运算;会选用恰当方法解决与分式有关的问题。
2、了解整数指数幂的意义和基本性质,能用幂的性质解决简单问题。
3、了解分式方程的概念,会解可化为一元一次方程的分式方程(方程中的分式不超过两个);会对分
式方程的解进行检验。
4、会运用分式方程解决简单的实际问题。
教学内容解析:
1、分式的乘法法则:
分式乘分式,用分子的积作积的分子,分母的积作积的分母.用式子表示为: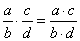
2、分式的除法法则:
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.用式子表示为: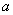
3、分式的乘方法则:
分式的乘方要把分子、分母分别乘方.用式子表示为: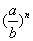 = =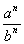 。 。
注:乘除混合运算可以统一为乘法运算;乘方与乘除混合运算同数的运算一样, 先乘方,再乘除. 先乘方,再乘除.
4、负整数指数幂的运算法则:
一般地,当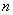 是正整数时, 是正整数时, 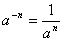 ( (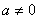 )……① )……①
注:
(1)此公式可以进一步变形: 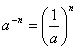 ( (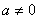 )……② )……②
(2)当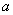 为整式时,使用公式①;当 为整式时,使用公式①;当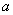 为分式时,使用公式②. 为分式时,使用公式②.
(3)指数概念扩大到全体整数后,幂的运算仍然成立,整指数幂的运算要综合幂的运算才能使复杂的
运算得到简化.
(4)负指数的科学记数法.
5、分式加减法的法则是:
同分母分式相加减,分母不变,把分子相加减.用式子表示是: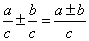
异分母分式相加减,先通分,变为同分母的分式,再加减.
用式子表示是: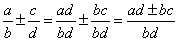
6、分式的混合运算顺序:
先乘方,再乘除,最后加减,有括号的先算括号内的.
7、分式方程:
分母中含未知数的方程叫做分式方程.
8、分式方程的解法:
解分式方程的基本思路是将分式方程化为整式方程,具体步骤:
(1)去分母:方程两边同乘最简公分母,约去分母,化为整式方程;
(2)解整式方程;
(3)验根:将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式
方程的解;否则,这个解不是原分式方程的解.
注:产生增根的原因:造成增根的原因就是解分式方程的第一步中去分母造成的.根据等式性质,方程两边同乘以(或除以)同一个非零数,所得结果仍是等式.这就是说,方程两边不能乘(除)以零,解方程的过程中,如果在方程的两边同时乘以值为零的整式,就会产生增根.
9、分式方程的应用:
(1)列分式方程解应用题的一般步骤:
①审题;②设未知数;③列分式方程;④解分式方程;⑤检验并写出答案.
(2)列分式方程解应用题的两步检验:
①验增根;②验符合实际.
经典例题解析:
【例1】 计算:
(1)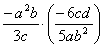 , (2) , (2)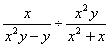 . .
分析:几个单项式相乘(相除),利用乘、除法的法则计算,约分,化为最简式子;分式中分子、分母是多项式,应分别先分解因式,再用乘、除法的法则计算,最后约分,化为最简式子.
解:(1)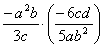 = =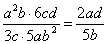 . .
(2)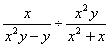 = =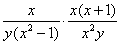 = =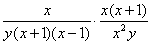 = =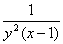 . .
【例2】计算:(1)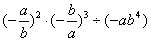 , (2) , (2)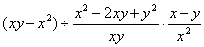 . .
分析:第(1)题是分式乘方与乘除混合运算,应先乘方再乘除;第(2)题分式中分子、分母是多项式,应分别先分解因式,再运用乘、除法的法则计算,最后约分,化为最简式子;乘、除法属于同一级运算,应按从左到右的运算顺序进行计算.
解:(1)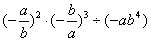 = =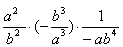 = =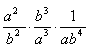 = =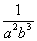 . .
(2)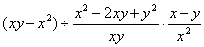 = =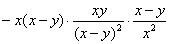 = =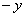 . .
【例3】 计算:(1)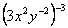 , (2) , (2)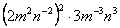 . .
分析:可先运用幂的运算性质进行计算,再化成正整数指数幂的形式.
解:(1)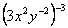 = =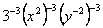 = =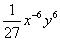 = =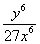 . .
(2)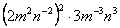 = =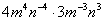 = =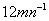 = =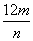 . .
【例4】一根约为1米长、直径为80毫米的光纤预制棒,可拉成至少400公里长的光纤.试问:1平方厘米是这种光纤的横截面积的多少倍?(保留两位有效数字)
分析:可先求光纤的横截面积,再列式计算.
解:光纤的横截面积为: 1×π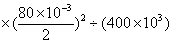 =4π =4π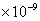 (平方米) (平方米)
∴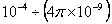 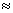 8.0 8.0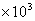 . .
答:平方厘米是这种光纤的横截面积8.0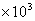 倍. 倍.
【例5】计算:(1)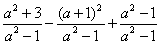 ,(2) ,(2)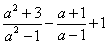 . .
分析:第(1)题中∵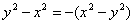 ,∴本题可化为同分母的分式;第(2)小题异分母分式的加减法运算,要通过通分化为同分母的分式运算,一个整式与分式相加减时,应把这个整式看作分母为1的一个式子. ,∴本题可化为同分母的分式;第(2)小题异分母分式的加减法运算,要通过通分化为同分母的分式运算,一个整式与分式相加减时,应把这个整式看作分母为1的一个式子.
解:(1)原式=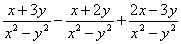
=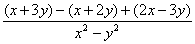 = =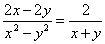 . .
(2)原式=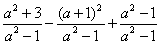 = =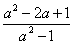 = =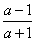 . .
【例6】已知: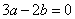 ,求下式的值 ,求下式的值
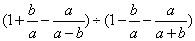 . .
分析:先化简,然后将已知条件变形代入求值.
解:原式=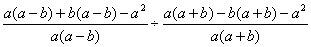
= = =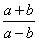 . .
当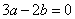 时, 时,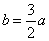 , ∴原式= , ∴原式=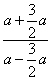 = =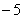 . .
【例7】 解分式方程 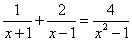 . .
分析:先将各分母分解因式,找出最简公分母,再去分母,转化为整式方程求解,要注意检验.
解:去分母,方程两边同乘以最简公分母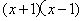 ,得 ,得
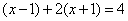
解这个整式方程得,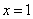
检验:把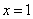 代入最简公分母 代入最简公分母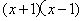 ,发现 ,发现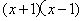 =0 =0
∴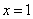 不是原方程的解,应舍去,∴原方程无解. 不是原方程的解,应舍去,∴原方程无解.
【例8】A、B两地相距40km,甲骑自行车从A地出发1小时后,乙也从A地出发,用相当于甲的1.5的速度追赶,当追到B地时,甲比乙先到20分钟,求甲、乙两人的速度.
分析:此题是行程问题,路程、速度、时间是行程问题的三要素.
路程:甲的路程是40km;乙的路程是40km; 速度:乙的速度=甲的速度的1.5倍
时间:乙走的时间=甲走的时间-1+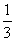
解:设甲的速度为xkm/h,则乙的速度为1.5xkm/h.
根据题意,得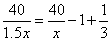 解这个方程得, 解这个方程得,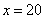
经检验知, 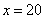 是原方程的根, 当 是原方程的根, 当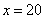 时, 1.5x =1.5 时, 1.5x =1.5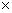 20=30 20=30
答:甲的速度为20 km/h.,乙的速度30 km/h.
|