|
轴对称
一、知识点
1、轴对称与轴对称图形
(1)轴对称图形
如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形。这条直线叫做这个图形的对称轴,这时,也说这个图形关于这条直线对称.
(2)轴对称
把一个图形沿着某条直线折叠,如果它能够与另一个图形完全重合,那么就说这两个图形关于这条直线对称。这条直线就是对称轴,两个图形中的对应点(即两个图形重合时互相重叠的点)叫做对称点。
(3)联系与区别.
区别:轴对称图形是说一个具有特殊性质的图形,是对一个图形说的;
轴对称是指两个图形之间的位置关系,是对两个图形说的.
联系:轴对称与轴对称图形都有对称轴,如果把轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成轴对称.
2、轴对称的性质
(1)关于某直线对称的两个图形全等;
(2)两个图形关于某直线对称,若它们的对应线段或延长线相交,则交点在对称轴上;
(3)两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
注:如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称。
类似地,轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.
3、线段的垂直平分线
(1)定义:
经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线).
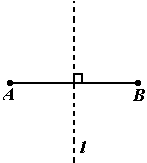
如下图,直线 为线段AB的垂直平分线。 为线段AB的垂直平分线。
(2)性质:
线段垂直平分线上的点与这条线段两个端点的距离相等.
逆定理(判定):与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
(3)用符号语言表述,
如图:
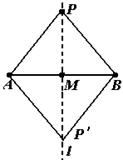
性质:∵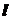 为线段AB垂直平分线,点P在 为线段AB垂直平分线,点P在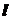 上。 上。
∴PA=PB
判定:∵PA=PB,P'A=P'B
∴过点P、P'的直线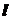 为线段AB的垂直平分线。 为线段AB的垂直平分线。
线段垂直平分线是到线段两端点距离相等的所有点的集合.
点在线段的垂直平分线上 点到线段两端的距离相等 点到线段两端的距离相等
4、简单的轴对称图形
(1)线段
①线段是轴对称图形
②对称轴有两条:一条是这条线段的垂直平分线;另一条是这条线段所在的直线。
③线段垂直平分线特征:是一条直线;垂直于已知线段;平分已知线段。
④线段的垂直平分线是和线段两个端点距离相等的所有点的集合。
(2)角是轴对称图形
①对称轴是角的平分线所在的直线。
②角的平分线性质与判定。
点在角平分线上 点到这个角的两边距离相等。 点到这个角的两边距离相等。
用符号语言表述,如图:
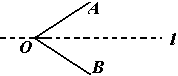
性质:∵P在∠AOB的平分线上,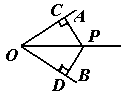
PD⊥OB于D,PC⊥OA于C,
∴PD=PC,
判定:∵PD=PC,PD⊥OB,PC⊥OA,
∴P在∠AOB的平分线上。
5、作轴对称图形
(1)轴对称变换
定义:由一个平面图形得到它的轴对称图形叫做轴对称变换.
轴对称变换同旋转变换、平移变换一样,都是图形变换的一种,轴对称变换的实质就是图形的翻折,而翻折问题往往可以看作是图形的全等问题,解这类问题的关键是利用图形的全等,找出对应线段对应角,挖掘题目的隐含条件,再利用结论使问题获解.
注意:经过变换以后,只是位置发生了变化,图形的形状和大小并未改变.
(2)作轴对称图形
例1.如图所示,点A和点B关于某条直线成轴对称,你能作出这条直线吗?

分析:我们只要连结点A和点B,画出线段AB的垂直平分线,就可以得到点A和B的对称轴。而由两点确定一条直线和线段垂直平分线的性质,只要作出到点A、B距离相等的两点即可。
解:如图所示:
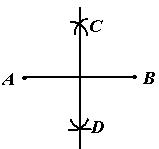
① 分别以点A、B为圆心,以大于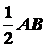 的长为半径作弧,两弧相交于C、D两点; 的长为半径作弧,两弧相交于C、D两点;
② 作直线CD。则CD为所求。
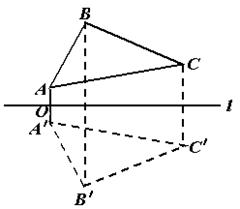
例2.如图,已知△ABC和直线l,作出与△ABC关于 直线l对称的图形。
分析:△ABC可以由三个顶点位置确定,则只要分别作这个顶点关于直线l的对称点,连结这些对称点,就得到要作的图形。
解:①过点A作直线l的垂线,垂足为点O,在垂线上截取OA'=OA,点A'就是点A关于l的对称点;
②类似地,作出点B、C关于直线l的对称点B',C';
③连结A'B'、B'C'、C'A'
则△A'B'C'为所求。
(3)关于坐标轴对称的点的坐标规律
①几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些点,就
可以得到原图形的轴对称图形;
②对于一些由直线、线段或射线组成的图形,只要做出图形中的一些特殊点(如线段端点)的对称
点,连接这些对称点,就可以得到原图形的轴对称图形.
点A(x1,y1)与B(x2,y2)关于x轴对称 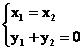
点A(x1,y1)与B(x2,y2)关于y轴对称 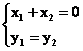
点A(x1,y1)与B(x2,y2)关于原点对称 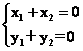
6、练习题:
1.下列图形哪些是轴对称图形,如果是,请找出所有对称轴。
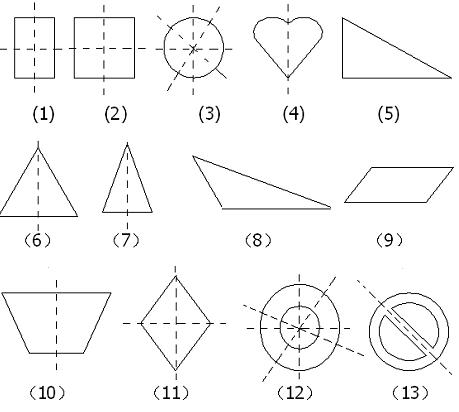
解答:(1)2条 (2)4条 (3)无数条 (4)1条 (5)不是轴对称图形
(6)1条 (7)1条 (8)不是轴对称图形 (9)不是轴对称图形
(10)1条 (11)2条 (12)无数条 (13)1条
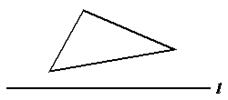
2.在下图这一组中找出它们所蕴含的内在规律,然后在横线的空白处设计一个恰当的图形.
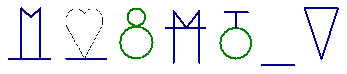
解答:
3.如图所示,把一个正方形三次对折后沿虚线剪下一角,则展开后所得的图形是( ).
 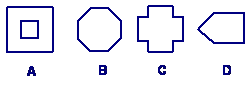
解答:C
4.如图,要在燃气管道 CD上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
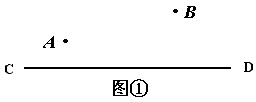
分析:实际问题→数学问题
在直线CD上找一点M,使AM+BM最短。若A、B在直线CD异侧,则连结AB与CD的交点即为所求点;而本题A、B两点在CD同侧,根据轴对称的性质可使问题转化为异侧。
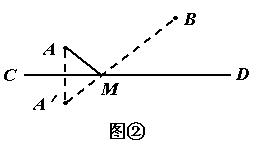 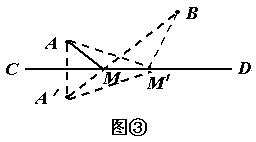
解:(1)作点A关于直线CD的对称点A'
(2)连结A'B交CD于点M
则M点为建抽水站处。
思考:你可否证明此时AM + BM最短?
略证:AM+BM=A′M+BM=A′B<A′M'+BM′=AM′+BM′
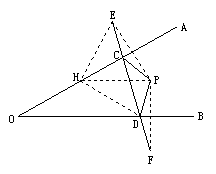
发展:在锐角∠AOB内有一定点P,试在OA、OB上确定两点C、D,使△PCD的周长最短.
略解:
分别作点P关于OA、OB的对称点E、F
连结EF,分别交OA、OB于点C、D
则点C、D为所求
5.(1)若点M(2,a)和点N(a+b,3)关于x轴对称,试求a,b的值;
(2)若点M(2,a)和点N(a+b,3)关于y轴对称,试求a,b的值.
解: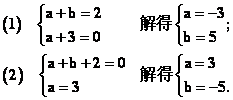
注:横轴横不变,纵轴纵不变
6.如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4)分别作出与四边形ABCD关于y轴和x轴对称的图形。
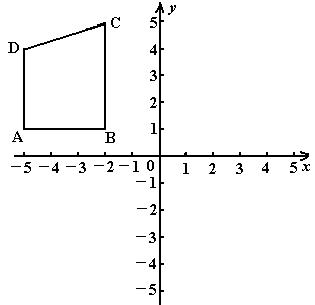
解:∵点(x,y)关于y轴的对称的点的坐标为(-x,y)
∴四边形ABCD关于y轴对称的点分别是A'(5,1),B'(2,1),C'(2,5),D'(5,4)
依次连结A'B'、B'C'、C'D'、D'A',就可得到四边形ABCD关于y轴对称的四边形A'B'C'D'
类似地,可作出与四边形ABCD关于x轴对称的图形。
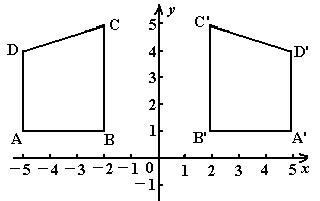
点评:对于此类问题,常先求出已知图形中的一些特殊点的对称点的坐标,描出并连结这些点即可。
|