4. 圆柱的侧面积 = 底面周长 × 高
5. 圆柱的表面积 = 侧面积 + 底面积 × 2
四、典型例题
例1、（圆柱和圆锥的特征）圆柱和圆锥分别有什么特点？
分析与解：长方体和正方体的六个面都是平面图形（长方形或正方形），而圆柱和圆锥除了底面是平面图形（圆）外，都有一个曲面。圆柱和圆锥的特征见下表。

例2、求下面立体图形的底面周长和底面积。

半径3厘米 直径10米
分析与解：根据圆的面积和周长计算公式计算圆柱和圆锥的底面周长和底面积。
圆柱：底面周长 3.14 × 3 × 2 = 18.84（厘米）
底面积 3.14 × 3 ² = 28.26（平方厘米）
圆锥：底面周长 3.14 × 10 = 31.4（米）
底面积 3.14 ×（10÷2）² = 78.5（平方米）

点评：圆柱和圆锥的底面都是圆，在计算它们的周长和面积时只要按照圆的周长和面积计算公式进行计算。

例3、判断：圆柱和圆锥都有无数条高。
错误解法：正确
分析与解：圆柱有无数条高，圆锥只有一条高。
正确解答：错误

点评：圆柱两个底面之间的距离叫做圆柱的高。两个底面之间有无数个对应的点，圆柱有无数条高。从圆锥的顶点到底面圆心的距离是圆锥的高。顶点和底面圆心都是唯一的点，所以圆锥只有一条高。

例4、（圆柱的侧面积）体育一个圆柱，底面直径是5厘米，高是12厘米。求它的侧面积。
分析与解：

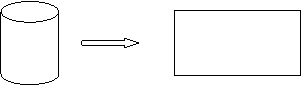
高

底面周长
沿着圆柱侧面的一条高剪开，将侧面展开，就得到一个长方形。这个长方形的长等于圆柱底面的周长，宽等于圆柱的高。因此，用圆柱的底面周长乘圆柱的高就得到这个长方形的面积，即圆柱的侧面积。
解答： 3.14 × 5 × 12 = 188.4（平方厘米）
答：它的侧面积是188.4平方厘米。
点评：圆柱的侧面是个曲面，不能直接求出它的面积。推导出侧面积的计算公式也用到了转化的思想。把这个曲面沿高剪开，然后平展开来，就能得到一个长方形，这个长方形的面积就是这个圆柱的侧面积。
例5、（圆柱的表面积）做一个圆柱形油桶，底面直径是0.6米，高是1米，至少需要多少平方米铁皮？（得数保留整数）

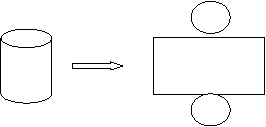分析与解：求铁皮的面积，就是求圆柱形油桶的表面积，即两个底面积和一个侧面积的和。

解答：底面积：3.14 ×（0.6÷2）² = 0.2826（平方米）
侧面积：3.14 × 0.6 × 1 = 1.884（平方米）
表面积：0.2826 × 2 + 1.884 = 2.4492（平方米）≈ 3（平方米）
答：至少需要铁皮3平方米。

点评：这里不能用四舍五入法取近似值。因为在实际生活中使用的材料要比计算得到的结果多一些。因此这儿保留整数，十分位上虽然是4，但也要向个位进1。

例6、（辨析）一个无盖的圆柱铁皮水桶，底面直径是30厘米，高是50厘米。做这样一个水桶，至少需用铁皮6123平方厘米。

分析与解：题目中是做一个无盖的圆柱铁皮水桶，只有一个底面。在计算铁皮面积时只要用圆柱的侧面积加上一个底面的面积。
解答：底面积：3.14 ×（30÷2）² = 706.5（平方厘米）
侧面积：3.14 × 30 × 50 = 4710（平方厘米）
表面积：706.5 + 4710 = 5416.5（平方厘米）
答：做这样一个水桶，至少需用铁皮5416.5平方厘米。

例7、（考点透视）一个圆柱的侧面积展开是一个边长15.7厘米的正方形。这个圆柱的表面积是多少平方厘米？

分析与解：圆柱的侧面积展开是一个正方形，即圆柱的高和底面周长都是15.7厘米。根据圆柱的底面周长可以算出底面积。

解答：底面半径：15.7 ÷ 3.14 ÷ 2 = 2.5（厘米）
底面积：3.14 × 2.5 ² = 19.625（平方厘米）
侧面积：15.7 × 15.7 = 246.49（平方厘米）
表面积：19.625 × 2 + 246.49 = 285.74（平方厘米）
答：这个圆柱的表面积是285.74平方厘米。
例8、（考点透视）一个圆柱形的游泳池，底面直径是10米，高是4米。在它的四周和底部涂水泥，每千克水泥可涂5平方米，共需多少千克水泥？

分析与解：要求水泥的质量，先要求水泥的面积。在圆柱形的游泳池的四周和底部涂水泥，涂水泥的面积是一个底面积加上侧面积。
解答：
侧面积：3.14 × 10 × 4 = 125.6（平方米）
底面积：3.14 × （10 ÷ 2）² = 78.5（平方米）
涂水泥的面积：125.6 + 78.5 = 204.1（平方米）
水泥的质量：204.1 ÷ 5 = 40.82（千克）
答：共需40.82千克水泥。

例9、（考点透视）把一个底面半径是2分米，长是9分米的圆柱形木头锯成长短不同的三小段圆柱形木头，表面积增加了多少平方分米？

分析与解： 锯圆柱形木头，表面积增加的部分是若干个相同的底面积。锯成三段，要锯两次，每锯一次增加两个面，锯了两次增加了四个面。
3.14 × 2 ² × 4 = 50.24（平方分米）
答：表面积增加了50.24平方分米。

点评：这是一道在实际生活中应用的题目，对于这一类题目，它的规律就是每切一次就增加两个面。但切的方式不同，增加的面也不同。如果是沿着底面直径把圆柱切成相同的两个部分，增加的面就是以底面直径和高为两邻边的长方形。

上一页  [1] [2]