|
初二数学周末练习1(分式方程的应用)
周末练习:
1、重量相同的两种商品,分别价值900元和1500元,已知第一种商品每千克的价值比第二种少300元,分别求这两种商品每千克的价值。
2、某客车从甲地到乙地走全长480Km的高速公路,从乙地到甲地走全长600Km的普通公路。又知在高速公路上行驶的平均速度比在普通公路上每小时快45Km,由高速公路从甲地到乙地所需的时间是由普通公路从乙地到甲地所需时间的一半,求该客车由高速公路从甲地到乙地所需要的时间。
3、从甲地到乙地的路程是15千米,A骑自行车从甲地到乙地先走40分钟后,B骑自行车从甲地出发,结果同时到达。已知B的速度是A的速度的3倍,求两车的速度。
4、一台甲型拖拉机4天耕完一块地的一半,加一台乙型拖拉机,两台合耕,1天耕完这块地的另一半。乙型拖拉机单独耕这块地需要几天?
5、A做90个零件所需要的时间和B做120个零件所用的时间相同,又知每小时A、B两人共做35个机器零件。求A、B每小时各做多少个零件。
6、某甲有25元,这些钱是甲、乙两人总数的20%。乙有多少钱?
答案与解析:
1.解:设第一种商品每千克的价值为x元,则第二种商品每千克价值为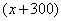 元, 元,
则: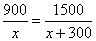
解得: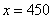 (元) (元)
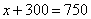 (元) (元)
答:这两种商品每千克的价值分别为450元和750元
2.解:设该客车由高速公路从甲地到乙地所需要的时间为x 小时,则
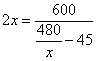
解得: (小时) (小时)
答:设该客车由高速公路从甲地到乙地所需要的时间为4小时。
3.解:设A的速度为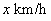 ,则B的速度为 ,则B的速度为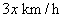 ,由题义得: ,由题义得:
40分钟 小时 小时
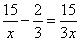
解得: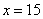

答:A的速度为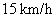 ,则B的速度为 ,则B的速度为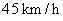
4.解:设乙型拖拉机单耕这块地需x天,则

解得: 天 天
答:乙型拖拉机单耕这块地需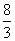 天 天
5.解:设A每小时做x个零件,则B每小时做 个零件, 个零件,
则 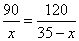
解得: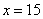
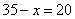
答:A每小时做15个零件, B每小时做20个零件。
6.解:设乙有x元钱,则:
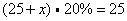
解得: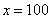 元 元
答:乙有100元
|