|
一次函数的图象与性质
知识要点:
1.一次函数的定义:
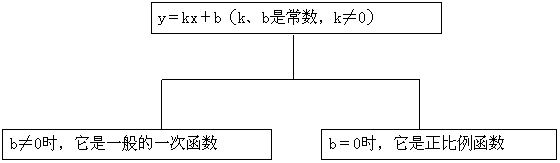
形如y=kx+b(k、b是常数,k≠0)的函数叫做一次函数。
注释:
(1)判断一个以x为自变量的函数(以后称关于x的函数)是不是一次函数?从其解析式的形式上看,
就是它能否化成关于x的一次二项式即kx+b的形式。其中一次项系数k必须是不为零的常数,常数
项b可以为任何常数。若k=0,它不是一次函数。
(2)要确定一个一次函数,可利用待定系数法,设y=kx+b为所求,只要依据已知条件求出k、b的值
即可。
2.一次函数与正比例函数的关系
在一次函数y=kx+b中,当b=0时,即y=kx(其中常数k≠0)是正比例函数。这时又称y与x成正比例,且比例系数为k。
3.通过正比例函数和一次函数的关系,类比正比例函数得到一次函数的图象与性质
(1)复习回顾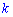 对正比例函数 对正比例函数 的的影响: 的的影响:
对于正比例函数y=kx,因为当x=0时,y=0;当x≠0时, 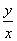 =k,所以正比例函数y=kx的图象是一条经过原点和(1,k)点的直线,又称为直线y=kx。 =k,所以正比例函数y=kx的图象是一条经过原点和(1,k)点的直线,又称为直线y=kx。
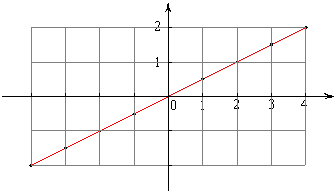
例如:正比例函数y=kx,它的图象是经过原点和(1, k)点的一条直线。
| 解析式 |
 (k为常数,且 (k为常数,且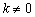 ) ) |
| 自变量取值范围 |
全体实数 |
| 图象 |
形状 |
过原点和(1,k)点的一条直线 |
| |
 |
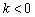 |
| 位置 |
经过一、三象限 |
经过二、四象限 |
| 趋势(从左向右) |
上升 |
下降 |
| 函数变化规律 |
y随x的增大而增大 |
y随x的增大而减小 | 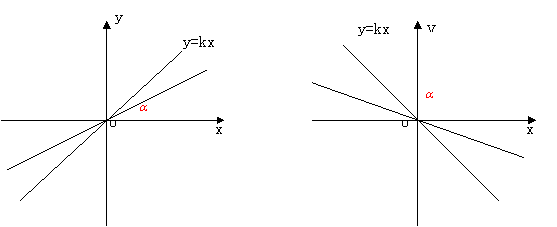
 时,直线 时,直线 的倾斜角为锐角; 的倾斜角为锐角;
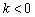 时,直线 时,直线 的倾斜角为钝角;且倾斜角的度数随k的增大而增大. 的倾斜角为钝角;且倾斜角的度数随k的增大而增大.
注:倾斜角即直线与x轴正方向的夹角。
(2)列表说明一次函数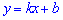 的图象与正比例函数 的图象与正比例函数 的图象之间的平移关系: 的图象之间的平移关系:
例如:

①当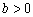 时,直线 时,直线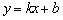 由直线 由直线 向上平移b的单位长度; 向上平移b的单位长度;
②当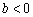 时,直线 时,直线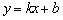 由直线 由直线 向下平移 向下平移 的单位长度. 的单位长度.
(3)对比得到一次函数的性质和图象:
因为一次函数y=kx+b的图象是一条直线,而由直线公理“两点确定一条直线”,所以一次函数y=kx+b的图象是过(0,b)点和(1,k+b)点的一条直线。作一次函数图象时,只要确定该图象上的两个点,再过这两点作直线,即为所求。
由函数图象的意义可知,坐标满足一次函数关系式y=kx+b的点P(x,y)都在它的图象上。反过来,一次函数y=kx+b图象上的任意一点P’(x,y),它的坐标也都满足y=kx+b。因此,一次函数y=kx+b的图象又称直线y=kx+b。
| 解析式 |
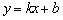 (k为常数,且 (k为常数,且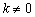 ) ) |
| 自变量取值范围 |
全体实数 |
| 图象 |
形状 |
过(0,b)和( ,0)点的一条直线 ,0)点的一条直线 |
| |
 |
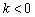 |
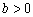 |
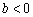 |
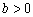 |
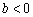 |
| 位置 |
经过第一、二、三象限 |
经过第一、三、四象限 |
经过一、二、四象限 |
经过二、三、四象限 |
| 趋势(从左向右) |
上升 |
下降 |
| 函数变化规律 |
y随x的增大而增大 |
y随x的增大而减小 | 
两条直线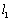 : :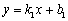 和 和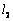 : :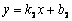 的位置关系可由其系数确定: 的位置关系可由其系数确定:
① 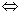 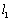 与 与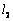 相交; 相交;
② ,且 ,且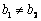 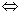 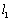 与 与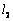 平行; 平行;
③ ,且 ,且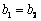 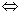 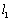 与 与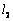 重合. 重合.
二、例题分析:
 1.下列函数中,正比例函数有( )一次函数有( ) 1.下列函数中,正比例函数有( )一次函数有( )
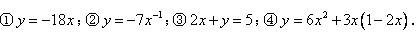
解答:①④是正比例函数,
①③④是一次函数。
注意:
1、正比例函数一定是一次函数;
2、看清函数“真正”的样子——化简后再判断
 2.已知关于变量s、t的关系式为3s+2t=5, 2.已知关于变量s、t的关系式为3s+2t=5,
(1)若t为自变量,则函数s=______,它是关于t的_______次函数;
(2)若s为自变量,则函数t=______,它是关于s的_______次函数;
(3)s-1与t-1的关系是__________,它的比例系数是__________。
解答: ,一, ,一, ,一,成正比例, ,一,成正比例,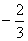
提示:3s+2t=5,
3(s-1)=-2(t-1),
s-1=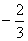 (t-1). (t-1).
 3.若函数 3.若函数 是关于x的一次函数,求k。并求出这个一次函数。 是关于x的一次函数,求k。并求出这个一次函数。
分析:从解析式的结构特征入手,① k≠ 0 ;②自变量x的次数为1;③常数项b可为任意实数——b为零时是正比例函数, b非零时是一次函数
解:∵函数 是关于x的一次函数, 是关于x的一次函数,
∴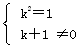
解之得,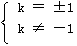
∴ k = 1
此时y=2x,它也是正比例函数
 4.已知一次函数y=-2x+1 4.已知一次函数y=-2x+1
(1)若自变量x的范围是-1≤x≤2,求函数值y的范围。
(2)若函数值y的范围是-1≤y≤2,求自变量x的范围。
分析:方法有二种:①画图法;②转化为代数问题(不等式)。
解:(1)∵y=-2x+1,又-1≤x≤2
∴x=0.5-0.5y
∴-1≤0.5-0.5y≤2
即 -1≤0.5-0.5y
0.5-0.5y≤2
解之,得-3≤y≤3
另解:
∵y=-2x+1,又-1≤x≤2
∴2≥-2x≥-4
∴3≥-2x+1≥-3
即 3≥y≥-3
即 -3≤y≤3
(2)∵-1≤y≤2
∴-1≤-2x+1≤2
解之,得-0.5≤y≤1
三、随堂练习:
1.若直线y=kx+b(k≠0)不经过第一象限,则k、b的取值范围是( )
A. k>0,b<0 B. k>0,b≤0 C. k<0,b<0 D. k<0,b≤0
答案:D
2.求过两点A(-3,-2)、B(1,4)两点的直线的解析式。
解:设直线的解析式为y=kx+b ,由已知,
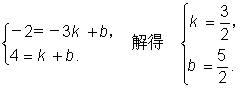
∴直线的解析式为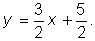
|