一、

题号	1	2	3	4	5	6	7	8	9	10
答案	AB	AC	BD	AC	BC	AD	BCD	CD	C	D

二、

11．向左；（2分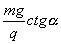）　 （3分）

12．308；（3分）　 0.40（2分）

13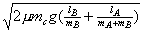．（5分）

三、

14．0.5mm；（2分） 0.001（2分）

15．（1）A、B球同时落地（1分），平抛运动的竖直分运动是自由落体运动.（2分）

　　 （2）通电导线在磁场里受到力的作用.（1分）

　　　　 金属棒摆动的角度更大些.（1分）

　　　　 通过金属棒的电流越大，它受的力越大（1分）

16．

(1)

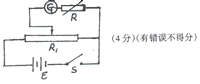
　　　　　 　　（2）C（1分）

　　　　　 　　（3）①调节电阻箱，伎其阻值较大，记下其值为R₁

　　　 　　　　　②调节滑动变阻器，伎G中有一适当的示数为I₁

　　　 　　　　　③固定滑动变阻器的滑动片的位置，调节电阻箱伎其阻值变为R₂，并　　　　　

　　　　　　　　　记下这时

　　　　 　　　　　G中的示数I₂ （3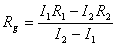分） 　（2分）

四、

17．（1）设：球B与球A相撞时球A的速度大小为V_A，球A的加速度大小为a.两球相

　　 碰表明：A球运动时间t恰好等于B球从高h=20m处运动到地面的时间；也表明球

　　 A和球B在水平方向的位移相等

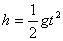　　 ………………………………………………………………（1） （2分）

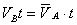　　 ……………………………………………………………（2） （2分）

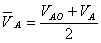　　 ………………………………………………………（3） （1分）

　　 由（1）（2）（3）并代入数据解出V_A=12m/s

　　 （2）V_A=V_AO+at ………………………………………………………（4） （2分）

　　 解出　 a=2m/s　　 　　　　　　　　　　　　　　　　　　　　　　（1分）

18．解：

　 （1）物体在跟位移的大小成正比，并且总是指向平衡位置的力作用下的振动叫简谐振　　

　　　　 动.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（2分）

（2）设小球运动中受到竖直向下的力为正，竖直向上的力为负，O是它的平衡位置，

Δl是小球在O点弹簧的伸长量.

在O点时，F_合=mg–kΔl=0解出mg=kΔl （2分）

以O点为原点建立坐标系ox，方向向下 （1分）

设小球在BOC之间运动的任意时刻的位移为x，该点小球受的力为：mg和

–k(x+Δl)　 （1分）

F_合=mg–kΔl=–kx ………………………………………………………（2分）

式中“–”表示力的方向与位移方向相反.由于x是任意时刻的位移，所以

它在任意时刻的回复力都跟位移x的大小成正比且方向总指向平衡位置（2分）

19．解：

光束从AB侧面垂直射入后不改变方向，射到AC侧面上的长度为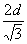…………（1分）

在AC侧面与空气交界面发生折射，入射角i=30°…………………………………（1分）

两种波长的光的折射角分别为r₁和r₂，（r₁>r₂）

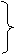
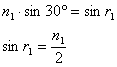　 　　…………………………………………………………（2分）

同理. 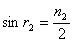……………………………………………………………………（1分）

光束经折射后，射到光屏MN上的长度是光束在AC侧面上长度的2倍，表明：从AC

侧面同一位置射出的两种波长的光由于折射角不同落到MN上的位置差等于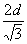，如图

所示.…………………………………………………………………………………（2分）

设.AC与MN间距离为L.有

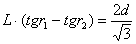　 …………………………（2分）　　　　　

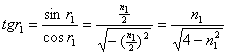………………（1分）

由理：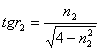

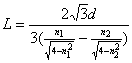∴………………………………（2分）

20．解：设A部分气体压强为p_A，体积为l_A • S.

　　　 设B部分气体压强为p_B，体积为l_B • S.

　　　 由活塞Ⅰ平衡：（p_A–p_o）S=G₂…………………………………………………（1分）

　　　 解出p_A=1.5p_o……………………………………………………………………（1分）

　　　 同理：由活塞Ⅱ平衡：（p_B–p_A）S=G₂ 解出p_B=2p_o…………………………（2分）

　　　 对气缸整体分析：当气缸对台秤面压力减为原来的一半时.

　　　　　 设拉力为F：

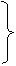
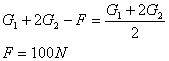　　　 　　………………………………………………（1分）

　　　 此时，设A部分气体的压强为p_A’，由活塞Ⅰ平衡：

　　　　　　　（p_p–p_A’）S=F–G₂……………………………………………………（1分）

　　　 p_A’=0.5p_o…………………………………………………………………………（1分）

　　　 ∵缓慢上提活塞，气体温度不变，由玻马定律

　　　　　　　　 p_Al_A= p_A’l_A’……………………………………………………………（1分）

　　　 l_A’=0.6m …………………………………………………………………………（1分）

　　　 同理：活塞Ⅱ平衡（p_B’–p_A’）S=G₂ ……………………………………………（1分）

　　　 p_B’=p_o………………………………………………………………………………（1分）

　　　 p_B • l_A= p_B’• l_B’……………………………………………………………………（1分）

　　　 l_B’=0.6m …………………………………………………………………………（1分）

　　　 设：活塞Ⅰ向上移动的距离为Δ，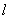

　　　　　　　 Δ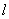=（l_A’+l_B’）–（l_A+l_B）=0.7m………………………………………（1分）

21．解：（1）设离子从M点射入磁场的速度方向与半径MR夹角为α.

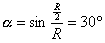　　 ………………………………（2分）

　　 依题意，在磁场中通过最大距离应是过M点的直径

　　 MRN.…………………………………………（1分）　　　　　　　图

　　 由于离子在磁场中运动受洛化兹力作用，运动轨迹

　　 是以MRN为弦长的圆弧并从N点射出磁场

　　　　　 ……………………………………………（1分）

　　 离子在磁场力作用下速度方向偏转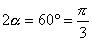………………………………（2分）

　　 ∴离子在磁场中运动的时间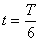

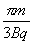　　　　　　　　　　　　　　=………………………………………………（2分）

（2）设离子在磁场中作圆周运动的半径为r.

　　　 由几何关系r=2R…………………………………………………………………（2分）

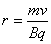　　　　　　　　 ………………………………………………………………（1分）

　　　　　　　　 v=Bq2R/m……………………………………………………………（1分）

　　　 由　　　 U_加q=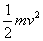…………………………………………………………（1分）

　　　 ∴　　　 U_加=2B²R²q/m…………………………………………………………（1分）

22．解：（1）设弹簧第一次恢复自然长度时B的速度为 v_B

　　　　　 以A、B弹簧为系统动量守恒

　　　　　 （m_A+m_B）v_o=m_B • v_o　　 (1)　　　　　　　　　　　　　　　　　（2分）

　　　　　 机械能守恒：

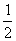　　　　　 （m_A+m_B）v_o+Ep=m_B • v_B²　　　 (2)　　　　　　　　　　　　（2分）

　　　　　 由（1）、（2）解出

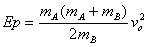　　　　　 　　　(3)　　　　　　　　　　　　　　　　（2分）

（2）设以后运动过程中B的速度为0时，A的速度为v_A此时弹簧的弹性势能为Ep’用动

　　　 量守恒

　　　 （m_A+m_B）v_o=m_B • v_o 　　（4）　　　　　　　　　　　　　　　　　　（2分）

　　　 机械能守恒

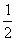　　　 （m_A+m_B）v_o+Ep=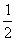m₄v_A² + Ep’　　　　 （5）　　　　　　　　　　（2分）

　　　 由（4）、（5）解出

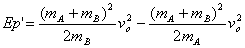　　　 　　　（6）

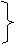　　　 ∵m_A<m_B

　　　 ∴Ep’<0　　　　　　　　　　　　　　　　　　　　　　　　　（3分）

　　　 弹性势能小于0是不可能的，所以B的速度没有等于0的时刻