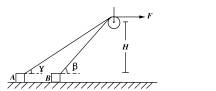
1.质量为m的物体右侧固定一个小定滑轮O，置于光滑水平面上，绳一端固定，另一端跨过滑轮与水平方向成θ角，大小为F的力拉物体，如右图所示，将物体由A拉至B点，共前进S，求外力F对物体所做的功
(命题说明：知识点——恒力做功；训练目的——对物体正确进行受力 分析，明确恒力做功的计算)
2.三角形劈质量为M，置于光滑水平面上，三S劈斜面光滑，将质量为m的物块置于三角劈斜面顶端由静止滑下，则在下滑过程中，M对m的弹力做功为w1，m对M的弹力对M做功w2，下列关系正确的是：
A.w1=0,w2=0
B.w1≠0,w2=0
C.w1=0,w2≠0
D.w1≠0,w2≠0
(命题说明：知识点——功的概念；训练目的——明确w＝F·S·cosα中S为对地位移，进一 步理解功的概念)
3.如右图所示，定滑轮至滑块高度为H，已知细绳拉力为F，滑块在时间t内沿水平地面由A点前进S米至B点，滑块在初末位置时细绳与水平方面夹角分别为α和β，求滑块由A点运动到B点过程中，拉力F对滑块做功的平均功率。
(命题说明：知识点——功率和平均功率的概念；训练目的——培养学生把变力做功转变为恒力做功的转化和迁移能力)
4.已知火车质量M=5.0×105kg，在一段平直轨道上以额定功率P行驶，在300秒内位移为2. 85×103m，同时速度由8m/s增加到火车在此轨道上行驶的最大速度17m/s，设火车阻力f大小恒定，求：(1)火车运动中所受阻力f的大小；(2)火车的额定功率P的大小。(命题说明：知识点——机车在额定功率F的运动，动能定理；训练目的：明确功能定理的内容，提高功率与动能定理综合应用能力)
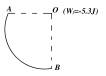5.如右图所示，A、B间的圆弧线表示位于竖直面内的
圆周轨道，A端与圆心等高，B端在圆心的正下方，已知轨道半径R＝1.0m，一质量为1.0kg的小物块自A端由静 止开始沿轨道下滑，当它滑到B点时，其速度大小为3.0m/s，求滑动摩擦力对小物块所做的功。
(命题说明：知识点——动能定理的应用；训练目的：变力做功转变为动能变化量，加深对动能定理的理解)
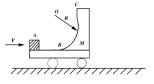
6.如右图所示，M=2kg的小车静止在光滑的水平面上，车面上AB段是长L=1m的粗糙平面，BC部分是半径为R=0.4m的光滑1/4圆弧轨道，今有一质量m=1kg的金属块静止在车面的A端，金属块与AB面的动摩擦因数μ＝0.3，若给A施加一水平向右，大小为I=5N·S的瞬间冲量，求 小车能获得的最大速度(g取10m/s2)
(命题说明：知识点——动量定理、动量守恒定律，动能定理的应用；训练目的——使学生 掌握动量守恒定律与动能定理综合应用能力)
7.光滑半圆上有两小球，质量分别为m和M，由细绳挂着，今由静止释放两小球，求小球m滑 至C点时速度(已知M＞m)
(命题说明：知识点——重力做功的特点、重力做功的一般应用；训练目的——掌握重力做 功与重力势能变化量间大小关系，加深对重力势能的理解)
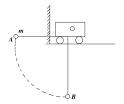
8.用汽车从井下提重物，重物质量为m，定滑轮高H，如图所示，已知汽车从A静止开始运动至B点时速度为vB，此时细绳与竖直方向夹角为θ，这一过程中细绳拉力做功多大?
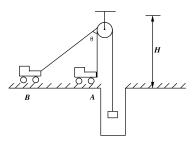
(命题说明：知识点——重力做功、动能定理、机械能的概念；训练目的——用动能定理求变力做功，并通过动能的变化建立与重力势能的变化，加深对机械能概念的理解)
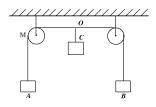
9.如右图所示，重物A、B、C质量相等，A、B用细绳绕过轻小滑轮相连接，开始时A、B静止，滑轮间细绳长0.6m，现将C物体轻轻挂在MN绳的中点，求：(1)C下落多大高度时速度最大?
(2)C下落的最大距离多大?
(命题说明：知识点——机械能守恒定律的应用；训练目的——掌握机械能守恒定律应用中隐含条件的发掘，提高机械能守恒与牛顿第二定律及受力分析的综合应用能力)
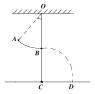
10.如右图所示，让摆球由A位置静止下摆，正好摆到最低点B位置时线被拉断，设摆线长l=1.6m，悬点到地面的竖直高度为H=6.6m，不计空气阻力，求：
(1)摆球落地时的速度
(2)落地点D到C点的距离(g=10m/s2)
(命题说明：知识点——机械能守恒定律、平抛运动的规律；训练目的——提高机械能守恒定律和平抛运动的综合能力)
11.光滑水平轨道上的小车质量为M=3kg，其下用细绳悬挂一质量m=2kg的小球(可视为质点)，细绳长度为L=0.8m，现手持小球向左拉使绳水平，使小车静止于轨道左端，轨道左端有挡板，然后从静止释放小球，g取10m/s2，求：(1)小球经最低点后向右摆动的最大高度?(2)小球从右侧最大高度回摆再次经过最低点时小车速度多大?(如图)
(命题说明：知识点——机械能守恒定律，动量守恒定律；训练目的——使学生进一步掌握动量守恒定律和机械守恒定律的应用，加深对动量守恒定律条件的判定的理解)
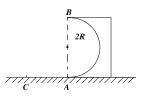
12.如右图所示，半径为R的半圆槽木块固定在水平地面上，质量为m的小球以某速度从A点无摩擦地冲上半圆槽，小球通过最高点B后落到水平地面上的C点，已知AC＝AB＝2R，求小球在 A点时的速度
(命题说明：知识点——机械能守恒定律，圆周运动，平抛运动；训练目的——圆周运动、平抛运动与机械能守恒定律综合应用能力的培养)
13.如右图所示，轻质细杆的两端分别固定质量均为m的两个小球A和B，细杆可绕O轴在竖直 平面内无摩擦地自由转动，BO＝2AO，将细杆从水平静止状态自由释放，求细杆转到竖直位置时对O轴作用力的大小和方向。
(命题说明：知识点——机械能守恒定律、向心力、线速度；训练目的——用机械能守恒定 律解决动力学问题)
14.如下图所示，质量为m的小球由长为l的轻绳固定在O点，今将小球水平拉至A点静止释放 ，在O点正下方何处钉一铁钉O′方能使小球绕O′点在竖直平面内做圆周运动?
(命题说明：知识点——圆周运动、机械能守恒定律；训练目的——加深对做圆周运动临界条件的理解，提高用机械能守恒定律解决圆周运动问题的能力)
15.质量为m的钢板与直立的轻弹簧的上端连接，弹簧下端固定在地上。平衡时，弹簧的压缩 量为xo，如右图所示，一物块从钢板正上方距离为3xo处的A点自由落下，打在钢板上并立即与钢板一起向下运动，已知物块质量也为m时，它们恰好能回到O点，若物块与钢板回到 O点时，还具有向上的速度，求物块向上运动到最高点与O点的距离。
(命题说明：知识点——机械能守恒定理、动量守恒、弹性势能、竖直上抛运动；训练目的 ——提高机械能守恒定律与动量守恒定律共同解决运动学问题的综合能力)
参考答案
1.WF＝FS(1+cosθ) 2.D 3.P=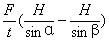
4.①f=2.5×104N，②P=4.25×105w 5.wf=-5·3J
6.vM=3m/s 7.vc=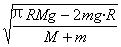
8.WT＝mgH(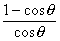
)+
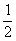mvB2sin2θ
9.①h=0.17m，②H=0.4m 10.vD=10.8m/s,s=4m
11.①h=0.48m,②v=3.2m/s 12.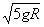
13.大小为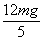
,竖直向下
14.OO′=
L 15.l=
xo
