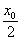1.以初速度vo=40m/s竖直向上抛出的物体，质量为4kg(g=10m/s2)则第2秒末的动量为 kg·m/s，第5秒末动量为 kg·m/s，从第2秒末到第5秒末动量的变化量为 kg·m/s。(命题目的：明确动量中的速度指瞬时速度，动量、动量的变化是矢量，“+”、“-”表示方向)
2.质量为0.4千克的小球以10m/s的速度从5m高的平台边缘水平抛出，小球落地时动量的大小和方向是
小球运动全过程中动量的变化是 (g=10m/s2)。(命题目的：知道动量的方向与瞬时速度的方向相同，掌握动量的变化的计算方法)
3.如果某物体做匀速圆周运动的动量大小为P，经过一段时间后其速度方向改变了θ角，它的动量变化的大小为 。(命题目的：了解曲线运动中动量变化的计算方法；掌握平行四边形定则作矢量图)
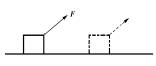
4.如右图，物体质量m=2kg，放在光滑水平桌面上，在恒定的牵引力F作用下由位置A运动 到位置B，速度由2m/s增加到4m/s，力F与水平面成60°角，求在此过程中力F的冲量。(命题目的：区分某个力的冲量与合外力的冲量两个不同的概念)。
5.一单摆摆球质量m=0.2kg，摆长l=0.5m，今将摆球拉离与竖直方向成50°角处由静止释放 ，求摆球运动到最低点的过程中重力的冲量和合外力的冲量。(g=10m/s2)(命题目的：知道恒力的冲量直接由I=F·t求，变力的冲力一般间接由I=ΔP求)
6.一个质点原来的动量为10kg·m/s，如果它受的作用力的方向跟初动量方向相同，F随时间 变化的规律如图所示，则在第5秒末该质点的动量为 kg·m/s，从第2秒末到第5 秒末的时间内质点受到的冲量为 N·S。
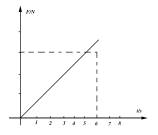
(命题目的：明确F-t图的物理意义，会根 据F-t图计算动量的变化或物体的冲量)
7.如下图，一辆质量为M的小车以速度v1在光滑水平面上运动，一质量为m速度为v2的 物体以俯角为θ的方向落到车上并埋在车里的砂中，此时小车的速度为 。
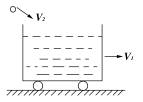
(命题目的：掌握沿某一方向动量守恒，则速度都指沿该方向的速度或在该方向的速度分量)
8.在水平轨道上放置一门质量为M的炮车，发射质量为m的炮弹，炮车与轨道间摩擦不计，当 炮身与水平方向成θ角发射炮弹时，炮弹相对炮身出口的速度为vo，则此时炮身后退的速度v′＝ 。
(命题目的：知道动量守恒中的速度都是对同一惯性参照系的速度)
9.质量为M的气球上有一质量为m的人，人和气球共同静止在离地面高度为h的空中，如果气球上有一质量忽略不计的软梯放下，以便让人能沿软梯安全地降到地面，则软梯至少要多长时才能达到上述要求?(命题目的：掌握动量守恒的条件是系统所受的合外力为零，而与相互作用的过程和作用力的性质无关)
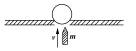
10.如右图所示，在支架的圆孔上放一质量为M的木球，一质量为m的子弹以速 度v从下面击中木球而穿出，使木球向上运动到h高处，求子弹穿过木球后上升的高度。(命题目的：明确碰撞、爆炸一类的相互作用其内力远远大于外力，外力可忽略不计，认为系统动量守恒)
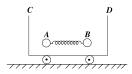11.如右图所示，一辆小车静止在光滑水平面上，在C、D两端置有油灰阻挡层、整辆小车质量1kg，在车的水平底板上放有光滑小球A和B，质量分别为mA=1kg，mB=3kg，A、B小 球间置一被压缩的弹簧，其弹性势能为6J，现突然松开弹簧，A、B小球脱离弹簧时距C、D端均为0.6m，然后两球分别与油灰阻挡层碰撞，并被油灰粘住，求：
(1)A、B小球脱离弹簧时的速度大小各是多少?
(2)整个过程小车的位移是多少?
(命题目的：掌握完全弹性碰撞的特点和完全非弹性碰撞的特点)
12.质量为m的钢板与直立轻弹簧的上端连接，弹簧的下端固定在地上，平衡时，弹簧的压缩 量为xo，如图所示一物块从钢板正上方距离为3xo的A处自由落下，打在钢板上并立刻与钢板一起向下运动，但不粘连，它们到达最低点后又向上运动，已知物块质量也为m时它们恰能回到O点，若物块质量为2m，仍从A处自由落下，则物块与钢板回到O点时还具有向上的速度，求物块向上运动到达最高点与O点的距离。(命题目的：会恰当地把复杂的物理过程抽象成几个有代表性的物理过程)
参考答案
1.80kg·m/s；-40kg·m/s；-120kg·m/s
2.4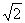
kg·m/s，与水平方向夹角45°，4kg·m/s
3.2P·sin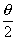
4.IF=8牛·秒
5.IG=0.69N·S;I合=0.039N·S 6.72.5N·S，52.5N·S
7.
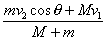8.
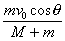
9.
10.
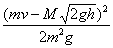
11.①vA=3m/s；vB=1m/s ②0.24m 12.
