|
复习一----光的反射与折射
一、知识结构
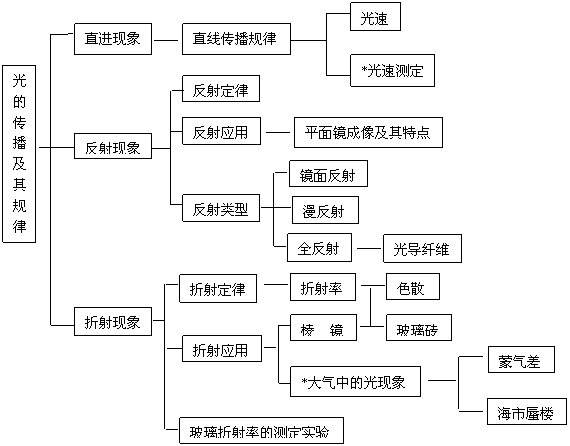
二、重点难点简析
1.光的传播规律的表述
本章所介绍的知识、实质上就是光在不同的条件下的传播规律,其表述形式分别如下所给出
(1) 光的直线规律
在同种均匀介质中光总是沿着直线传播。应该注重到,在真空中,光沿直线传播的速率均为C=3×108m/s,在其它介质中,光的沿直线传播的速率 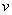 <C,且不同的色光在同一种介质中沿直线传播的速率不同,频率越高,速率越小。 <C,且不同的色光在同一种介质中沿直线传播的速率不同,频率越高,速率越小。
(2) 光的反射定律
光照射到两种介质的界面上,一部分将返回原来的介质,其传播规律遵从所谓的反射定律,定律的表述要把握如下要点:反射光线、入射光线、法线共面;反射光线与入射光线分居法线两侧;反射角等于入射角。应该注重到,反(入)射角指的是反(入)射光线与法线间的夹角。
(3)光的折射定律
光照射到两种介质的界面上,可能有一部分光将穿过介质界面进入新的介质,其传播规律遵从所谓的折射定律,定律的表述要把握如下要点:折射光线、入射光线、法线共面;折射光线与入射光线分居法线两侧;入射角与折射角的正弦之比等于常数。应该注重到,光从光疏(密)介质斜射入光密(疏)介质时,入射角将大(小)于折射角;而光从光密介质射向光疏介质,且入射角足够大时,将不会发生光的折射现象。
 2.光的传播规律所引起的相关光现象 2.光的传播规律所引起的相关光现象
(1)“影”与“食”的现象。
光线在均匀介质中沿直线传播时被不透明的物体挡住,
在物体后面所形成的暗区称为影。影又分为本影和半影,
在本影区域内完全看不到光源发出的光;在半影区域内
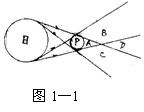
能看到光源上一部分所发出的光。如图1—1所示,太阳作
为光源发出的光在不透明的物体P后面留下了影,其中区
域A称为半影;区域B、C称为半影;区域D则称为伪本影。
 日食和月食也是光的直进规律所引起的自然光现象。若图1—1中的P是月球,则地球上的某区域处在区域A内将看到日全食;处在区域B或C内将看到日偏食;处在区域D内将看到日环食。若图1—1中的P是地球,则月球处在区域A内将看到月全食;处在区域B或C内将看到月偏食;由于日、月、地的大小及相对位置关系决定看月球不可能运动到区域D内,所以不存在月环食的自然光现象。 日食和月食也是光的直进规律所引起的自然光现象。若图1—1中的P是月球,则地球上的某区域处在区域A内将看到日全食;处在区域B或C内将看到日偏食;处在区域D内将看到日环食。若图1—1中的P是地球,则月球处在区域A内将看到月全食;处在区域B或C内将看到月偏食;由于日、月、地的大小及相对位置关系决定看月球不可能运动到区域D内,所以不存在月环食的自然光现象。
(2)平面镜成像时物与像关于镜面对称的现象
正因为光在发生反射现象时遵从从光的反射定律,
图1—2中的入射角  与反射 与反射 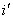 相等,所以才形成 相等,所以才形成
了物点 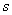 与像点 与像点  关于镜面M对称的特征。 关于镜面M对称的特征。
(3)全反射现象与色散现象
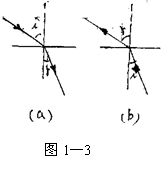 光在穿过介质界面发生折射现象时遵从光的折射定律。 光在穿过介质界面发生折射现象时遵从光的折射定律。
假如光从光疏介质斜射入光密介质时,入射角  大于折射角 大于折射角 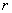 , ,
如图1—3中(a)所示。假如光从光密介质斜射入光疏介质时,入射角  小于折射角 小于折射角 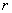 ,如图1—3中(b)所示。这就使得在光从光密介质射向光疏介质的情况下,随着入射角 ,如图1—3中(b)所示。这就使得在光从光密介质射向光疏介质的情况下,随着入射角  的逐渐增大,折射角 的逐渐增大,折射角 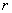 将率先增大到90O,进而发生所谓的全反射现象。 将率先增大到90O,进而发生所谓的全反射现象。
由于在光的折射定律中,入射角与折射角的正弦比等于
两种介质的相对折射率 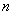 ,而对于不同频率的色光 ,而对于不同频率的色光 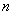 的取值一 的取值一
 般不同,所以,复色光在光的折射过程中将发生所谓的光的色散现象。 般不同,所以,复色光在光的折射过程中将发生所谓的光的色散现象。
三、典型例题分析
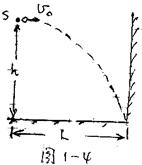
例1.如图1—4所示,S为点光源,
若从S所在处沿水平方向方向抛出一个
小球,试证实:小球在竖直墙壁上的影子
将做匀速运动。若抛出点高度为h,抛出
时水平初速度大小为 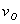 ,小球最终着地时 ,小球最终着地时
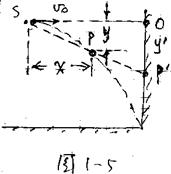 的水平位移为L,求影子沿墙壁下降的速度。 的水平位移为L,求影子沿墙壁下降的速度。
分析:小球抛出后做平抛运动,当小球的水平和
竖直位移大小分别为x和y而运动到P点处时,
对应的墙上的影子运动到 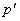 点,如图1—5所示, 点,如图1—5所示,
于是由平抛运动的规律及光的直进规律可以确定
影子的位移 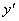 与x、y间的关系,从而最终解决问题。 与x、y间的关系,从而最终解决问题。
解:由平抛运动的规律及光的直进规律所确定的几何关系依次可得
x= 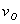 t t
y= 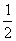 gt2 gt2
 = = 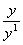
于是可将影子的位移 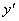 表为时间t的关系为 表为时间t的关系为
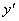 = = 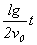
因为影子的位移 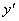 表为时间t的一次函数,所以可以判定:影子沿竖直墙壁下降的运动是匀速直线运动,其中 表为时间t的一次函数,所以可以判定:影子沿竖直墙壁下降的运动是匀速直线运动,其中 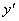 与t的比例系数即为影子下降的速度大小,即 与t的比例系数即为影子下降的速度大小,即
 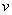 = = 
例2.如图1—6所示,MO和NO是两面
互成角度的平面镜,S是点光源,P为某定点,
试画出S出发先后经MO和NO反射而最终
经过P点的光路。
 分析:若S1是S在MO中的像,而S2是S1在 分析:若S1是S在MO中的像,而S2是S1在
NO中的像,则S、S1、S2、P四个点就将能确定所求的光路。
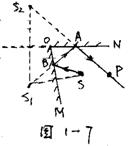
解:所画光路如图1—7所示,而画法如下:
(1)取点S1与S关于MO对称;
(2)取点S2与S1关于NO对称;
(3)连接S2P交NO于A点;
(4)连接S1A交MO于B点
(5)连接SB
(6)按照画光路的要求标明各条线的虚实,及标上光的实际传播路线上的箭头。
 例3.某水池中水的实际深度为h,水的折射率为n,沿垂直于水面方向向下看,水的视深为多大? 例3.某水池中水的实际深度为h,水的折射率为n,沿垂直于水面方向向下看,水的视深为多大?
分析:画出从水面正上方向下看水池底部的观察
光路如图1—8所示,水池底部某点S发出的沿垂直于
水面四周小范围内的光线折射出水画并射入观察者的眼
睛,使观察者感觉到的水池底部的S点在  处,在此基 处,在此基
础之上运用折射定律及相应的几何关系即可求解。
解:由光的折射定律,得
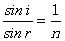
由相应的几何关系,得
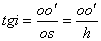

考虑到观察者沿垂直于水面方向观察时,图1—8中的入射角  和折射角 和折射角 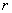 均很小,而当角度很小时,又有 均很小,而当角度很小时,又有

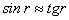
由此即可解得
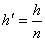
例4.已知水的折射率为 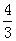 ,光在真空中传播速度为3×108m/s,则:光在水中的传播速度为_____________m/s;光从水中射向空气时发生全反射现象的临界角为_____________。 ,光在真空中传播速度为3×108m/s,则:光在水中的传播速度为_____________m/s;光从水中射向空气时发生全反射现象的临界角为_____________。
分析:此例的求解应当依据折射率与光速的关系
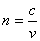
和临界角的计算公式:

解:由相应的规律依次可得
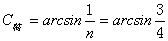
所以,应依次填上2.25×108, 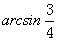 。 。
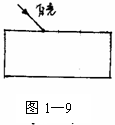
例5.如图1—9所示,一束白光从平行玻璃砖
上表面斜射入,试定性画出这束光的传播路线,并指
出从玻璃砖下表面射出的光束的基本特征。
 分析:光射过平行玻璃砖时,实际上就是在其上,下表面两次发生折射现象,考虑到从上表面射入玻璃砖时是从光疏介质射入光密介质,而从下表面射出玻璃砖时又是从光密介质射入光疏介质,同时考虑到上,下表面相互平行,于是不难得:从下表面射出的光线与从上表面射入的光线平行而只是产生一个侧移;另外还应该注重到白光中包含了从红到紫的各种色光,而不同色光在同一种介质中偏折的程度各不相同,所以,从下表面射出的光是按照颜色散开的彩色光带。 分析:光射过平行玻璃砖时,实际上就是在其上,下表面两次发生折射现象,考虑到从上表面射入玻璃砖时是从光疏介质射入光密介质,而从下表面射出玻璃砖时又是从光密介质射入光疏介质,同时考虑到上,下表面相互平行,于是不难得:从下表面射出的光线与从上表面射入的光线平行而只是产生一个侧移;另外还应该注重到白光中包含了从红到紫的各种色光,而不同色光在同一种介质中偏折的程度各不相同,所以,从下表面射出的光是按照颜色散开的彩色光带。
解:定性画出的光的传播路线如图1—10所示,
从下表面射出的光束的特征如下:
(1)从下表现射出的是彩色光带,
这是由于玻璃砖的色散的作用;
(2)彩色光带的左侧是紫光,
右侧是红光,这是由于红光在玻璃中
传播速度最大,折射率最小,折射时偏折的程度最小;
(3)射出的各种色光均平行,
且平行于射入的白光,这是由于平行玻璃砖只能使光
的传播路线产生一个侧移的特征所致。
练 习
一、选择题(每题3分,共36分)
1.关于光的反射,正确的说法是 ( )
A.反射定律只适用于镜面反射
B.漫反射不遵循反射定律
C.假如甲从平面镜中能看到乙的眼睛,那么乙一定也能通过平面镜看到甲的眼睛
D.反射角是指反射线和界面的夹角
2.无影灯是由多个大面积光源组合成的,关于其照明效果,正确的说法是 ( )
A.没有影子 B.没有半影 C.没有本影 D.有半影和本影
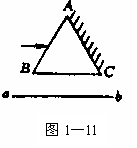 3.一束光线沿与水平方向成40O角的方向传播,现放一平面镜,使入射光线经平面镜反射后沿水平方向传播,则此平面镜与水平方向所夹锐角为 3.一束光线沿与水平方向成40O角的方向传播,现放一平面镜,使入射光线经平面镜反射后沿水平方向传播,则此平面镜与水平方向所夹锐角为
A.20O B.40O C.50O D.70O
4.关于日食和月食,正确的说法是 ( )
A.在月球本影中的人,能看到月全食
B.在月球半影中的人,能看到日偏食
C.月球在地球的半影内,出现月偏食
D.月球在地球的本影内,出现月全食
5.如图1—11所示,一束白光射向正三棱镜的AB面,由于AC面为反射镜,
光线经AC反射后,从BC射出射到光屏上,则在光屏上可以看到 ( )
A.彩色的光带,a端为红光,b端为紫光
B.彩色的光带,b端为红光,a端为紫光
C.略为变宽的白光
D.由于入射光的入射角不同,可能导致不同的结果,即上述三种情况均有可能
6.已知光线穿过介质I、II、III时的光路如图1—12所示,
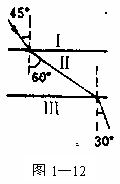 下列说法中正确的是 ( ) 下列说法中正确的是 ( )
A.介质II是光密介质
B.介质I的折射率最大
C.介质Ⅲ的折射率比I大
D.光在介质III中光速最小
7.一束单色光自真空射向折射率为2的介质的界面上形成反射光束和折射光束,下列说法中正确的是 ( )
A.反射光和折射光的颜色相同
B.反射光和折射光的光速相同
C.反射光和折射光的波长相同
D.反射光和折射光的频率相同
8.一条光线通过在水中的球形空气泡,表示出射光线的可能光线是图1—13中的( )
A.a B.b C.c D.d
9.一束光从空气射向折射率为 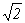 的某种玻璃的表面,如图1—14所示, 的某种玻璃的表面,如图1—14所示,  代表入射角,则 ( ) 代表入射角,则 ( )
A.当  >45O时,会发生全反射现象 >45O时,会发生全反射现象
B.无论入射角  是多大,折射角 是多大,折射角 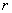 都不会超过45O 都不会超过45O
C.欲使折射角 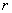 =30O,应以 =30O,应以  =45O的角度入射 =45O的角度入射
D.当  = = 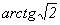 时,反射光线跟折射光线恰好互相垂直 时,反射光线跟折射光线恰好互相垂直
10.如图1—15所示,半径为R的半圆形透明材料,折射率 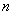 =2.0,一束平行光从空气以垂直于其底面的方向射入,则 ( ) =2.0,一束平行光从空气以垂直于其底面的方向射入,则 ( )
A.所有光线都能通过这种材料
B.只有距圆心O两侧R/2范围内的光线才能通过
C.射出的光束会形成发散光束
D.射出的光束会形成会聚光束
11.一个均匀的透明圆柱体切成横截面如图1—16所示的柱体,一束平行光从空气垂直AB平面射入(不考虑二次反射),则
A.II部分光线一定能全部射出
B.II部分光线能否全部射出与透明体的折射率有关
C.I、III两部分光线一定能全部射出
D.I、III两部分光线能否全部射出与透明体的折射率有关
12.一强点光源放在10㎝厚的玻璃板下表面上,在玻璃板的下面可以看到点光源的四周一圆形暗圈,若玻璃的折射率为n=1.5,则暗圈的直径约为 ( )
A.36㎝ B.30㎝ C.18㎝ D.15㎝
二、填空题(每题5分,共30分)
13.光在真空中的传播速度是________m/s,在折射率为1.5的介质中,光的传播速度是________m/s.
14.光线从真空射入某媒质时,若光线与媒质表面的夹角为30O,反射光线与折射光线刚好垂直,则该媒质的折射率为________.
15.在一个圆形轻木塞的中心插上一根大头针,然后把它倒放在水面上,调节针插入的深度,使观察者不论在什么位置都刚好不能看到水下的大头针,如图1—17所示,量出针露出的长度为d,木塞的半径为r,则可求出水的折射率为________.

16.一块透明体折射率为n=2的玻璃制成的,其截面如图1—18所示,其中 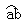 半径为R,ac边垂直于bc边,且∠aoc=60O,当一束平行黄光垂直照射到ac上时,ab圆弧部分的外表面只有一部分是黄亮的,其余是暗的,则黄亮部分的弧长是________. 半径为R,ac边垂直于bc边,且∠aoc=60O,当一束平行黄光垂直照射到ac上时,ab圆弧部分的外表面只有一部分是黄亮的,其余是暗的,则黄亮部分的弧长是________.
17.如图1—19所示,等腰三棱镜的底角为30O,两束平行光对称地垂直于底面射向三棱镜,则出射的两束光之间的交角为________.(已知三棱镜的折射率为 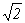 ) )
18.如图1—20所示,直角玻璃棱镜中∠A=70O,入射光线垂直于AC面,则光线从棱镜第一次射入空气时的折射角为________,并作出光路图.( 已知玻璃的折射率为 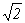 ) )
三、计算题(  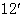 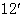 = =  ) )
19.一个大游泳池,池底是水平面,池水深1.2m,有一直杆竖竖立于池底,浸入水中部分杆是全长的一半,当太阳光以与水平方向成37O角射在水面上时,测得杆在池底的影长为2.5m,求水的折射率.
20.在水平地面上有一点光源S,被一不透明的罩子遮住,在罩子的正上方开一小孔,一束光通过此小孔竖直射到距离地面高为3m的水平放置的平面镜上,如图1—21所示,若平面镜忽然绕水平轴O开始顺时针匀速转动,在0.1s内转动30O角,由镜面反射到水平地面上的光斑在0.1s末沿地面移动的速度多大?此时光斑位置距点光源S有多远?在0.1s内光斑在水平地面上移动的平均速度是多大?
 21.如图1—22所示,玻璃立方体放在空气中,其折射率为1.50,平行光线从立方体的一面入射后投射到另一面,问:(1)这条光线能否从这个侧面射出?(2)假如这条光线从这个侧面射出,那么玻璃的折射率应满足什么条件? 21.如图1—22所示,玻璃立方体放在空气中,其折射率为1.50,平行光线从立方体的一面入射后投射到另一面,问:(1)这条光线能否从这个侧面射出?(2)假如这条光线从这个侧面射出,那么玻璃的折射率应满足什么条件?
参考答案
1.C 2.C 3.AD 4.BD 5.A 6.CD 7.AD 8.A 9.BCD
10.BD 11.BC 12.C 13.3×108,2×108 14.  15. 15. 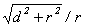
16. 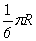 17.30O 18.45O(图略) 19.n= 17.30O 18.45O(图略) 19.n= 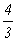
20.  , , 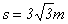 , , 
21.(1)不能 (2)n< 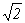
|