|
动量守恒定律及其应用·典型例题精析
[例题1] 平静的湖面上浮着一只长l=6m,质量为550 kg的船,船头上站着一质量为m=50 kg的人,开始时,人和船均处于静止.若船行进时阻力很小,问当人从船头走到船尾时,船将行进多远?
[思路点拨] 以人和船组成的系统为研究对象.因船行进时阻力很小,船及人所受重力与水对船的浮力平衡,可以认为人在船上行走时系统动量守恒,开始时人和船都停止,系统总动量为零,当人在船上走动时,无论人的速度如何,系统的总动量都保持为零不变.
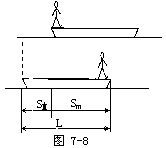
[解题过程] 取人运动方向为正方向,设人对岸的速度为v,船对岸的速度为V,其方向与v相反,由动量守恒定律有
0=mv+(-MV).
解得两速度大小之比为
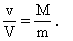
此结果对于人在船上行走过程的任一瞬时都成立.
取人在船上行走时任一极短时间Δti,在此时间内人和船都可视为匀速运动,此时间内人和船相对地面移动的距离分别为ΔSmi=viΔti和ΔSMi=ViΔti,由此有
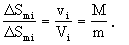
这样人从船头走到船尾时,人和船相对地面移动的总距离分别为
Sm=∑ΔSmi,SM=∑ΔSMi.

由图中几何关系可知Sm+SM=L.这样,人从船头走到船尾时,船行进的距离为
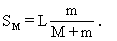
代入数据有
SM=0.5 m.
[小结] 本题表明,在动量守恒条件得到满足的过程中,系统任一瞬时的总动量保持不变.
[例题2] 如图7-9示,物块A、B质量分别为mA、mB,用细绳连接,在水平恒力F的作用下A、B一起沿水平面做匀速直线运动,速度为v,如运动过程中,烧断细绳,仍保持力F大小方向不变,则当物块B停下来时,物块A的速度为多大?
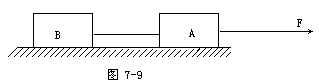
[思路点拨] 以A和B组成的系统作为研究对象.绳子烧断前,A、B一起做匀速直线运动,故系统所受外力和为零,水平方向系统所受外力计有拉力F,物块A受到地面的摩擦力fA,物体B受到地面的摩擦力fB,且F=fA+fB.绳烧断后,直到B停止运动前F与fA、fB均保持不变,故在此过程中系统所受外力和仍为零,系统总动量保持不变.所以此题可用动量守恒定律求解.
[解题过程] 取初速v的方向为正方向,设绳断后A、B的速度大小分别为v′A、v′B,由动量守恒定律有
(mA+mB)v=mAv′A+mBv′B.

[小结] (1)本题表明动量守恒定律不仅可以解决相互作用时间极短的碰撞等类问题,也可以解决过程持续时间较长的问题.
(2)本题解法体现了应用动量守恒定律解题的特点和优点:由于动量守恒定律只考虑系统相互作用前后的状态,而不考虑相互作用过程中各瞬时的细节,所以解决问题十分简便,这也是物理学中其他守恒定律(例如机械能守恒定律)也都具有的特点和优点.本题也可用牛顿运动定律(结合运动学公式)或应用动量定理来求解,但都要繁复一些.但本题若问B停下所用的时间是多少,动量守恒定律就无能为力了,就得应用牛顿运动定律(结合运动学公式)或动量定理来求解了.
(3)非凡要注重A、B组成的系统动量保持不变仅维持到B刚好停下为止,此后系统动量则不再守恒,因B停下后其所受的摩擦力fB变为零,系统所受外力和不再为零,不再满足动量守恒条件.
[例题3] 总质量均为M的甲乙两船在湖面上以相同速度v沿一直线鱼贯匀速航行如图7-10所示,现自甲船向后以相对甲船速度u水平向乙船抛一质量为m的沙袋,若不计水的阻力,求抛接沙袋后,甲、乙两船的速度各为多大?
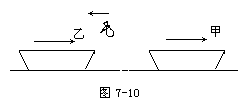
[思路点拨] 本题涉及两个相互作用过程.过程Ⅰ:将沙袋从甲船抛出;过程Ⅱ:沙袋落在乙船上.因不计水的阻力,对于这两个过程若分别以甲船与沙袋及乙船与沙袋为系统,动量均守恒.
[解题过程] 以甲、乙两船原来速度方向为正方向,设抛接沙袋后,甲、乙两船速度分别为v′甲,v′乙.
对于过程Ⅰ,以甲船和沙袋作为系统,由动量守恒有
Mv=(M-m)v′甲-m(u-v′甲).
(因题中给出的是沙袋抛出时相对甲船的速度u,所以沙袋离开甲船时相对岸的速度为u-v′甲.)

对于过程Ⅱ,以乙船和沙袋为系统,由动量守恒有
Mv-m(u-v′甲)=(M+m)v′乙.
将上面解得的v′甲代入解得

表明抛接沙袋后,甲船速度增加,乙船速度减小,乃至为零或反向.
[小结] (1)应用动量守恒定律解题时,应明确所应用的系统和过程.
本题求乙船速度也可将甲、乙两船及沙袋作为系统,对抛接全过程(包括过程Ⅰ和过程Ⅱ)应用动量守恒定律,得到
2Mv=(M-m)v′甲+(M+m)v′乙.
将解得的v′甲代入解得v′乙,结果相同,这表明动量守恒定律也适用于多个物体组成的系统的复杂相互作用过程.
(2)应用动量守恒定律时,应注重定律表达式中各速度应相对于同一惯性参考系,本题取地面.
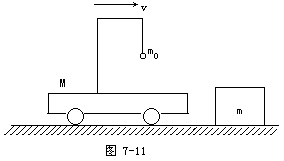
[例题4] 在质量为M的小车中挂有一单摆,摆球的质量为m0,小车(和单摆)以恒定的速度v0沿光滑水平面运动,与位于正对面的质量为m的静止木块发生碰撞,碰撞的时间极短,在碰撞过程中,下列情况可能发生的是
[ ]
A.小车和摆球的速度都变为v1,木块的速度变为v2,满足
(M+m0)v0=(M+m)v1+mv2
B.小车、木块、摆球的速度都发生变化分别变为v1、v2、v3,满足
(M+m0)v0=Mv1+mv2+m0v3
C.摆球的速度不变,小车和木块的速度变为v1和v2,满足
Mv=Mv1+mv2
D.摆球的速度不变,小车和木块的速度变为v′,满足
Mv=(M+m)v′
[思路点拨] 由于小车与木块发生碰撞的时间极短,碰撞时仅小车与木块间发生相互作用,使小车与木块的动量速度发生变化,而在这极短时间内,摆球和小车水平方向并没有通过绳发生相互作用,所以小车与木块碰后瞬时,小球仍保持原来的速度而未来得及变化.
[解题过程] 小车与木块碰撞刚结束时,球仍保持原来的速度,仅小车与木块由于相互作用,各自动量发生改变,所以选项A、B是错误的.
取小车(不包括摆球)和木块作为系统,碰撞前后动量守恒,但小车与木块碰后可能分离,也可能结合在一起,所以选项C、D中两情况都可能发生.
[小结] 本题表明了碰撞这一物理现象发生时间极短这一的特点,由于碰撞现象的这一特点,可以使碰撞问题的解决通过近似得以简化.
[例题5] 在光滑水平直轨道上停着一辆质量为M的平板车,车上有n个质量均为m的人,如每人相对于车以速率u相继快跑并相继跳离车的一端,试问他们相继快跑跳离车后使车得到的速度,与他们同时以同样速率u快跑并同时跳离车后使车得到的速度相比,哪个大?
[思路点拨] 如n人一起以相同速率跳离车,跳离车过程中n人同时与车发生相互作用,如将这n人与车作为一系统,这一过程中,系统水平方向不受外力,系统动量守恒.
如n人相继跳离车时,这n人相继与车发生相互作用.因题设每人跳离车时相对车速率u相等,但由于每人跳离车时车速不同,所以每人跳离车时相对地面的速率是不同的,此种情况下,应应用动量守恒定律依次讨论每人跳离车的过程,方可做出结论.
[解题过程] 若n人同时快跳以相对车速率u同时跳离车,设跳离后,车获得速度为v,取人跳离后车速方向为正.由动量守恒有
0=Mv+nm(v-u).
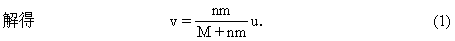
若n人相继快跑并相继以相对车速率u跳离车,设第一人跳离车时车速为v1,第二人跳离车时车速为v2,……第n人跳离车时车速为vn,仍取车速方向为正,对每一人跳离车过程.由动量守恒有
[M+(n-1)m]v1+m(v1-u)=0,
[M+(n-2)m]v2+m(v2-u)=[M+(n-1)m]v1,
[M+(n-3)m]v3+m(v3-u)=[M+(n-2)m]v2,
……
Mvn+m(vn-u)=(M+m)vn-1.
将以上各式相加,得
Mvn+m(v1-u)+m(v2-u)+…+m(vn-u)=0,
或 Mvn=m(u-v1)+m(u-v2)+…+m(u-vn)
=nmu-mv1-mv2-…-mvn.

比较(1)、(2)两式可知vn>v,即n人相继跳离时,使车获得速度比同时跳离时大.
[小结] (1)应用动量守恒定律解决过程较复杂的问题时,应注重系统与过程的选取.
(2)动量守恒定律表达式中的各速度应是相对同一惯性系的速度,此题取的是地面.
|