|
动量守恒定律·典型例题解析
【例1】 如图52-1所示,在光滑的水平面上,质量为m1的小球以速度v1追逐质量为m2,速度为v2的小球,追及并发生相碰后速度分别为v1′和v2′,将两个小球作为系统,试根据牛顿运动定律推导出动量守恒定律.
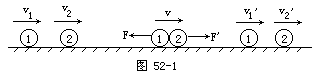
解析:在两球相互作用过程中,根据牛顿第二定律,对小球1有:F

-F′,所以F·Δt=-F′·Δt,m1Δv1=-m2Δv2,即m1(
v1′-v1)=-m2(v2′-v2),整理后得:m1v1+m2v2=m1v1′+
m2v2′,这表明以两小球为系统,系统所受的合外力为零时,系统的总动量守恒.
点拨:动量守恒定律和牛顿运动定律是一致的,当系统内受力情况不明,或相互作用力为变力时,用牛顿运动定律求解很繁杂,而动量定理只管发生相互作用前、后的状态,不必过问相互作用的细节,因而避免了直接运用牛顿运动定律解题的困难,使问题简化.
【例2】 把一支枪水平地固定在光滑水平面上的小车上,当枪发射出一颗子弹时,下列说法正确的是
[ ]
A.枪和子弹组成的系统动量守恒
B.枪和车组成的系统动量守恒
C.子弹、枪、小车这三者组成的系统动量守恒
D.子弹的动量变化与枪和车的动量变化相同
解析:正确答案为C
点拨:在发射子弹时,子弹与枪之间,枪与车之间都存在相互作用力,所以将枪和子弹作为系统,或枪和车作为系统,系统所受的合外力均不为零,系统的动量不守恒,当将三者作为系统时,系统所受的合外力为零,系统的动量守恒,这时子弹的动量变化与枪和车的动量变化大小相等,方向相反.可见,系统的动量是否守恒,与系统的选取直接相关.
【例3】 如图52-2所示,设车厢的长度为l,质量为M,静止于光滑的水平面上,车厢内有一质量为m的物体以初速度v0向右运动,与车厢壁往返碰撞n次后,静止在车厢中,这时车厢的速度为_______,方向与v0的方向_______.
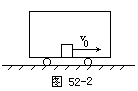
点拨:不论物体与车厢怎样发生作用,碰撞多少次,将物体与车厢作为系统,物体与车厢间作用力是内力,不改变系统的总动量,同时这一系统所受的合外力为零,系统的总动量守恒,以v0为正方向,有mv0=(M+m)v′.
【例4】 一辆列车的总质量为M,在平直的水平轨道上以速度v匀速行驶,忽然最后一节质量为m的车厢脱钩,假设列车所受的阻力与车的重量成正比,机车的牵引力不变,当脱钩的车厢刚好停止运动时,前面列车的速度为多大?
点拨:以整列列车为系统,不管最后一节车厢是否脱钩,系统所受的外力在竖直方向上重力与轨道给系统的弹力相平衡,在运动方向上牵引力与系统所受的总的阻力相平衡,即系统所受的外力为零,总动量守恒.
参考答案

跟踪反馈
1.在光滑水平面上有两个质量不等的物体,它们之间夹一被压缩的弹簧,开始时两物用细绳相连,烧断细绳后两物体
[ ]
A.在任何时刻加速度大小相等
B.在任何时刻速度大小相等
C.在任何时刻动量大小相等
D.在任意一段时间内,弹簧对两物体的冲量相同
2.沿一直线相向运动的甲、乙两质点,作用前动量分别是P1=10kg·m/s,P2=-18kg·m/s,作用后甲的动量为-1kg·m/s,不计任何外界阻力,则作用后乙的动量为
[ ]
A.-29kg·m/s
B.29kg·m/s
C.-7kg·m/s
D.7kg·m/s
3.质量为490g的木块静止在光滑水平面上,质量为10g的子弹以500m/s的速度水平射入木块并嵌在其中,从子弹刚射入木块至与木块相对静止的过程中,木块增加的动量为_______kg·m/s,它们的共同运动速度为_______m/s.
4.质量为120t的机车,向右匀速滑行与静止的质量均为60t的四节车厢挂接在一起运动,由于四节车厢的挂接,使机车的速度减小了3m/s,求机车在挂接前的速度.
参考答案
1.C 2.C 3.4.9;10 4.4.5m/s;方向向右
|