|
引力常量的测定
1.下列说法正确的是( )
A.海王星和冥王星是人们依据万有引力定律计算的轨道而发现的
B.天王星是人们依据万有引力定律计算的轨道而发现的
C.天王星的运行轨道偏离根据万有引力定律计算出来的轨道,其原因是由于天王星受到轨道外面其他行星的引力作用
D.以上均不正确
2.一艘宇宙飞船绕一个不知名的行星表面飞行,要测定该行星的密度,仅仅只需测定( )
A.运行周期
B.环绕半径
C.行星的体积
D.运动速度
3.一颗小行星绕太阳做匀速圆周运动的半径是地球公转半径的4倍,则这颗小行星运转的周期是( )
A.4年
B.6年
C.8年
D. 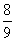 年 年
4.用m表示同步卫星的质量,h表示它离地面的高度,  表示地球半径, 表示地球半径,  表示地球表面的重力加速度, 表示地球表面的重力加速度, 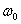 表示地球自转角速度,则同步卫星所受地球对它的万有引力大小是( ) 表示地球自转角速度,则同步卫星所受地球对它的万有引力大小是( )
A. 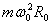
B. 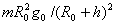
C. 
D. 
5.设行星绕恒星的运行轨道是圆,则其运行周期T的平方与其运动轨道半径R的三次方之比为常数,即 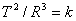 ,那么k的大小( ) ,那么k的大小( )
A.只与行星质量有关
B.只与恒星质量有关
C.与行星及恒星的质量均有关
D.与恒星的质量及行星的速率有关
6.中子星是由密集的中子组成的星体,具有极大的密度,通过观察已知某中子星的自转角速度ω=60πrad/s,该中子星并没有因为自转而解体,根据这些事实人们可以推知中子星的密度。试写出中子星的密度最小值的表达式为 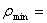 ____________________,计算出该中子星的密度至少为_____________________ ____________________,计算出该中子星的密度至少为_____________________ 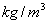 。(假设中子通过万有引力结合成球状星体,保留2位有效数字)。 。(假设中子通过万有引力结合成球状星体,保留2位有效数字)。
7.登月舱在离月球表面112km的高空绕月球运行,运行周期为120.5min,已知月球半径为  ,试估算月球的质量。 ,试估算月球的质量。
参考答案
1.A、C与万有引力定律相关的一些史实资料要记下来。
2.A 由万有引力充当宇宙飞船在行星表面绕行的向心力得
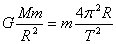
∴外星的密度 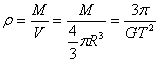
∴只需测出宇宙飞船的运行周期即可。
3.C由  得 得 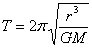
∴行星与地球绕太阳公转周期之比为:
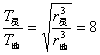
∴ 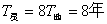
4.B、C、D在地球表面上, 
解得  ,在h高处,物体所受的万有引力为 ,在h高处,物体所受的万有引力为
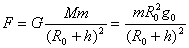
∴B对。
万有引力等于向心力  ,D对。 ,D对。
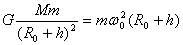
解得 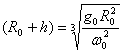 ,代入上式 ,代入上式
 ,C对。 ,C对。
5.B由 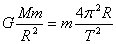 得 得 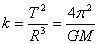
∴k的大小由恒星的质量决定。
6. 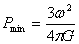 
提示:中子星表面处的任一质量微元△m
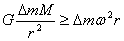
所以  , ,
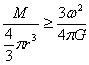 , ,
故  , ,
代入数据 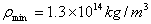
7.解:设舱的质量为  ,月球的质量为 ,月球的质量为 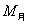 ,月球的半径为 ,月球的半径为 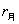 ,舱离月球表面的距离为r, ,舱离月球表面的距离为r,
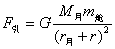
舱绕月球做圆周运动,所以向心力的大小为
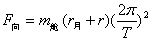
因为 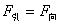
所以 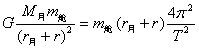
得 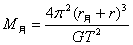
将已知的数据代入上式,可得月球的质量
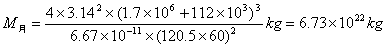
|