|
初二数学周末练习1(全等三角形与三角形全等的判定)
周末练习:
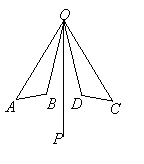
1、已知:如图, 是 是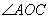 和 和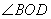 的平分线, 的平分线,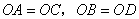 . .
求证:(1)△OAB≌△OCD; (2)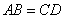 . .
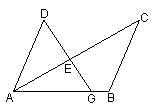
2、如图,G是线段AB上一点,AC和DG相交于点E. 请先作出∠ABC的平分线BF,交AC于点F;然后证明当:AD∥BC,AD=BC,∠ABC=2∠ADG时, DE=BF. DE=BF.
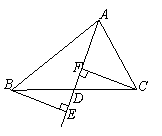
3、如图,已知BE⊥AD,CF⊥AD,且BE=CF.请你判断AD是△ABC的中线还是角平分线?请说明你判断的理由.
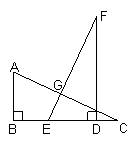
4、如图,已知AB⊥BC于B,EF⊥AC于G,DF⊥BC于D,BC=DF. 求证:AC=EF.
5、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形, 在同一条直线上,连结 在同一条直线上,连结 . .
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:DC⊥BE .
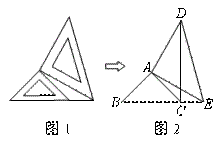

答案与解析:
1、由OP是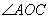 和 和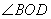 的平分线, 的平分线,
可得∠AOP=∠COP,∠BOP=∠DOP
 ∠AOB=∠DOC(等量减等量差相等). ∠AOB=∠DOC(等量减等量差相等).
又 OA=OC,OB=OD, OA=OC,OB=OD,
(1) △AOB≌△COD(SAS); △AOB≌△COD(SAS);
(2) AB=CD(全等三角形的对应边相等). AB=CD(全等三角形的对应边相等).
2、解: 作出的BF见右图,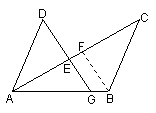
证明:由BF是∠ABC的角平分线,得:
∠ABC=2∠FBC
又∠ABC=2∠ADG(已知)
所以 ∠FBC=∠ADG
由AD∥BC 得,∠BCF=∠DAE
又因为AD=BC
所以 △ADE≌△CBF(ASA)
 DE=BF(全等三角形的对应边相等) DE=BF(全等三角形的对应边相等)
3、解:AD是中线,
证明:由已知BE⊥AD,CF⊥AD可得∠BED=∠CFD=90°
又 ∠BDE=∠CDF(对顶角相等) ∠BDE=∠CDF(对顶角相等)
 ∠DBE=∠DCF(同角或等角的余角相等), ∠DBE=∠DCF(同角或等角的余角相等),
再根据BE=CF可得:
△ BDE≌△CDF(AAS),
从而得到BD=CD,即AD是中线.
4、证明:由EF⊥AC于G,DF⊥BC于D,AC和DF相交,可得:
∠C=∠F(同角或等角的余角相等),
又已知BC=DE,
又∠EDF=∠ABC=90°
证得△ABC≌△EDF(角边角),
从而得到AC=EF(全等三角形的对应边相等).
注:在一个图形中,有多个垂直关系时,常用“同角或等角的余角相等”来证明两角相等,或用“等量代换”证明垂直关系.
5、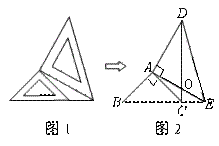 解:(1)△BAE≌△ACD 解:(1)△BAE≌△ACD
证明: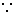 ∠BAC=∠EAD=90° ∠BAC=∠EAD=90°
 ∠BAC +∠CAE=∠EAD +∠CAE ∠BAC +∠CAE=∠EAD +∠CAE
即 ∠BAE=∠CAD
又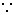 AB=AC,AE=AD, AB=AC,AE=AD,
 △ABE≌△ACD(SAS) △ABE≌△ACD(SAS)
(2)由(1)得∠BEA=∠CDA,
又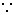 ∠COE=∠AOD ∠COE=∠AOD
 ∠BEA+∠COE =∠CDA+∠AOD=90° ∠BEA+∠COE =∠CDA+∠AOD=90°
则有∠DCE=180°- 90°=90°,
所以DC⊥BE.
|