中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料
|
|
| 中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
二．填空题（本题共3小题，共14分．将答案填写在空格里．）
 11．（6分） 一金属圆环用一绝缘细线悬挂于O点，下部有垂直于纸面向里的匀强磁场，如图5所示。现将环向右拉出磁场至A点，这时细线与竖直方向的夹角为θ，使环由静止开始下摆，下摆时金属圆环所在平面始终垂直于磁场，则（1）环由A点摆至右侧最高点B的位置 （填 “高于”、“低于”或“等于”）A点的位置；（2）若想求出环由A摆至右侧最高点B的过程中，环中产生的焦耳热，需要测量的物理量有_____________ （在以下几个选项中选出正确的，填序号），写出产生的焦耳热的表达式 。
①磁感强度B ②环的面积S ③O点到环心的长度L④由A到B所用的时间t ⑤AB两点的高度差h ⑥当地的重力加速度g ⑦环的电阻R ⑧环的质量m
 12、（4分）如图所示，质量为m的带电小滑块能沿着竖直墙滑下，磁感应强度为B的匀强磁场的方向水平并与小滑块运动方向垂直。若小滑块带正电量q，滑块与墙间的动摩擦因数为µ，则小滑块下落的最大速度为___________。
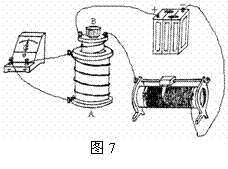
13、（4分）右图是某同学研究电磁感应中所产生的感应电流方向的实验电路，A是一只空心的线圈，B是一只带铁芯的线圈，所带的铁芯可以从线圈B中抽出，A、B两线圈的绕向如图11所示，它们之间是相互绝缘的，已知电流从灵敏电流计G的“ ”极进入时，灵敏电流计的指针向右偏转。现要让灵敏电流计的指针向左偏转，可以进行的操作有（至少写出两种方法（1） ； （2） 。 三．计算题（本题共4小题，共46分．解答时必须写出文字说明、图形、方程和重要演算步骤，只写最后结果的不得分．有数值运算的结果要写出数值和单位．）
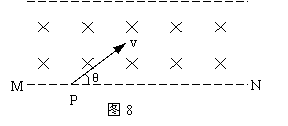 14. (10分)如图8所示，直线MN的上侧有垂直于纸面向里的有界匀强磁场，磁场的上边界与MN平行，磁感应强度为B. 质量为m，带电量为-q的粒子以速度v从MN上的p点射入磁场，入射方向与MN间夹角为θ.沿MN方向磁场范围足够大，要使粒子能从MN上的某点射出磁场，磁场上边界到下边界MN的距离至少应为多大?
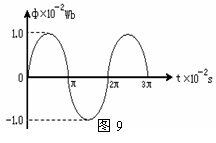 15．（12分）小型发电机内的矩形线圈在匀强磁场中以恒定的角速度ω绕垂直于磁场的固定轴转动．线圈匝数n=100．穿过每匝线圈的磁通量φ随时间按正弦规律变化，如图9所示．发电机内阻r=5.0Ω，外电路电阻R=95Ω．求：（1）串联在外电路中的交流电流表（内阻不计）的读数；（2）一个周期内，线圈发热产生的热量；（3）线圈从中性面起转动半周的过程中，流过R的电量．
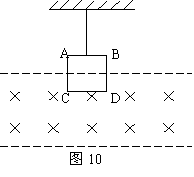 16．（10分）如图10所示，正方形线框ABCD的总电阻R为0.4Ω，质量m为0.1kg，边长为0.4m，两虚线之间是垂直于线框平面向里的匀强磁场，磁场上限（上面一条虚线）正好过AC和BD的中点，磁感应强度从2T开始以5T／s的变化率均匀增大，当磁感应强度为多大时，悬线的拉力为零？（AB边水平）
 17．（14分）如图11所示，水平放置的光滑平行金属导轨宽度L=0.2m，质量为0.1㎏的金属导线ab垂直于导轨放在其上。整个装置放在方向竖直向下，磁感应强度B=0.5T的匀强磁场中。ab直导线在F=2N的水平向右的恒力作用下由静止开始向右运动，电路的总电阻R=0.05Ω。求：
（1）导体棒运动的最大速度是多大？ （2）ab导线运动速度v=5m/s时，ab的加速度是多大？ （3）当ab达到最大速度时，撤去恒力F，以后感应电流在电阻R上还能产生多少热量？
高二年级第二学期半期考试 物理试题（答案） 一 选择题（每题4分，共40分。少选得2分，错选、不选不得分）
| 题号
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 答案
| D
| CD
| BC
| CD
| AC
| B
| B
| A
| BC
| ABC |
二．填空题（共14分）
11、（每空2分）低于 ⑤⑥⑧ mgh
12、（4分）mg/μqB
13、将线圈B从线圈A中拔出；将线圈B中的铁芯拔出；将滑动变阻器的滑动触头向左滑动（至少写出两项，每一项2分，共4分）
三、计算题
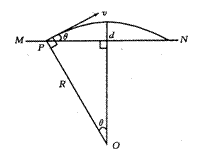14、解：粒子在磁场中的运动轨迹如图所示，设轨道半径为R，则有
（4分）
（1分）
设上、下边界的最小距离为d，由图可知
（5分）
15、解：由图象可得：Φm=1.0×10-2Wb,（1分）
T=2π×10-2s
∴ω=2π/T=100rad/s（1分）
而Eｍ=nBSω=nΦmω= 100×1.0×10-2×100
=100V（1分）
（1） （1分）
由闭合电路欧姆定律可得： 
（2分）
所以，电流表的读数为0.707A
（2）线圈产生的热量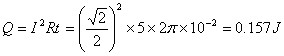 
（2分）
（3）流过R的电量 
（3分）
代入数据可得：q=2×10-2C（1分）
16、解：根据法拉第电磁感应定律， 
（3分）
（2分） 
（3分）
（2分）
17、解：⑴ 
（4分）
（1分）
⑵由牛顿第二定律可得：
（4分）
（1分）
⑶根据能量受恒可得： 
（4分）
| |
B. 
C. 
D. 
3、LC回路中电容器两极间电压u随时间t变化的关系如图1所示，则
D. ef将往返运动
10、如图4所示，两水平金属板之间的区域内，存在电场强度为E的匀强电场和磁感应强度为B的匀强磁场. 已知从左向右水平射入板间的电子，沿直线穿过了板间区域，则E和B的方向可能是
