中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料
|
|
| 中文域名: 古今中外.com
英文域名：www.1-123.com 丰富实用的教育教学资料 |
| |
| |
| |
|
|
[例题] 1．以一定的初速度竖直向上抛出一个小球，小球上升的最大高度为h，运动中空气阻力大小恒为f，则小球从抛出点到再回到原抛出点的过程中，空气阻力对小球做的功应为：（ ） A、A、零； B、 B、 -fh； C、C、-2fh； D、D、-4fh。 [解析] 小球在上升和下降过程中空气阻力都是做负功，所以全过程空气阻力对小球所做的功应为Wf=Wf上 Wf 下= —fh （—fh）= —2fh 2．质量为m的物体被额定功率为P的升降机提起，物体的最大速度能达到v0，那么，当物体的速度为v（v<v0）时，它能获得的最大加速度am等于多少？ [解析] 设运动阻力为f ，升降机对物体的拉力为F，有 F—f = ma P额=fv0=Fv 所以a= 3．质量为2kg的物体静止在水平地面上，对物体施以水平拉力使它开始沿直线运动，在10s未将拉力撤去，其水平拉力F？物体与水平面间的滑动摩擦系数
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| t/s |
|
| 30 |
|
| 0 |
|
| 10 |
分析：由图象看出物体在前10s做匀加速直线运动，
a1=1m/s2后20s做匀减速直线运动，a2=-0.5m/s2。前10s
内物体在水平方向上受到拉力和摩擦力的作用，后20s
内只受摩擦力作用。
解： F-f = ma1 ①
-f = ma2 ②
由①②得：
F = m（a1-a2）
=2（1 0.5）= 3N
f = -ma2 = -2×（-0.5）=1N
f = 
N = mg = 
= 0.05
|
| 300 |
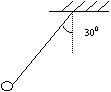4．质量为0.1kg的小球，用长1m的轻绳挂于O点，把小球拉到与竖直方向的夹角为300的位置后，静止释放，求小球在最低位置的速度大小。
解：选取小球为研究对象，小球受到重力和绳子拉力的作用，
但只有重力做功，小球机械能守恒选择小球在最低位置的水
平面为零势能参考平面
mv2 0 = 0 mg 
（1-Cos300）
V = 
= 
m/s
= 1.62m/s
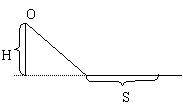
5．如图一个物体从一个光滑斜面下滑至底部，水平面是粗糙的，最后停在离斜面底部的距离为S处，求水平面的滑动摩擦系数
解： 我们把整个过程作为研究对象，根据动能定理
|
| H |
|
| S |
|
| O |
0-0 = mgH-fs
f = 
[练习]
1．放在光滑水平面上的静止物体，在水平拉力的作用下，移动了距离s，假如拉力改为和水平面成300的力F2，移动的距离为2s，已知拉力F1和F2对物体所做的功相等，则F1和F2的大小的比为
A．2：1 B． 
：1 C．3：1 D． 
：1
2．用木棒击球，球重为1N，击球所用的力是5N，球被击出后移动2m，在此过程中，木棒击球所做的功是
A．2J B．10J C．12J D．条件不足，无法确定
3．物体受到相同的水平拉力F作用，分别在光滑的和粗糙的水平面上通过 了相等的距离，则
A．在光滑水平面上，力F做的功多些
B．在粗糙水平面上，力F做的功多些
C．在光滑水平面上，力F的平均功率大些
D．在粗糙水平面上，力F的平均功率大些
4．假如在行驶过程中，汽车甲比汽车乙实际消耗的功率大，则可以判定
A．甲的速率比乙大 B．甲的牵引力比乙大
C．甲做功比乙快 D．甲做功比乙多
5．质量为m的炮弹飞出炮筒的速度为v，炮筒长为 ，设火药在炮筒中对炮弹的推力恒定不变，则火药压力对炮弹做功的平均功率是
A．mv3/4 B．mv3/2
C．mv2/ D．mv2/4
6.质量和速度大小都相同的两个物体，它们的
A．动能、动量都一定相同； B．动能相同，动量不一定相同
C．动量相同，动能不一定相同 D．动能、动量都可能不相同
7．单摆的摆球质量为0.5kg，当摆球摆到某个位置时具有1.0Ｊ的动能，那么它在这个位置上具有动量的大小是
A．0.5kg·m/s B．1.0kg·m/s
C．2.0kg·m/s D．3.0kg·m/s
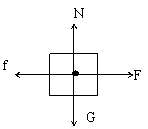
8.质量为0.5kg的物体静止在水平面上，受到一个大小为3N的水平拉力作用后开始运动，运动中所受滑动摩擦阻力为2N，此拉力作用力2s后，其大小为1N而方向不变，继续拉物体，求全过程中拉力对物体所做的总功，物体总位移为多大？外力最大功率为多大？
9．物体质量m = 2kg，在水平面上作直线运动，图4—2
是物体运动的v—t图线，在0~5s内，物体受到一个
|
| 15 |
|
| 10 |
|
| 5 |
|
| 0 |
|
| t（s） |
|
| v（m/s） |
|
| 1 |
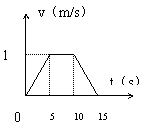恒定的拉力F = 0.8N，物体在整个运动过程中所受摩擦
阻力相等。求：（1）摩擦力等于多少？（2）在0~5s，
5~10s，10~15s三段时间中拉力作功各为多少？合力做
功各为多少？物体机械能增量各为多少？
10．质量为3kg的铅球，由静止开始自由落下，经1s落入砂坑，在砂坑内经0.1s铅球停止运动，求铅球克服砂的平均阻力做了多少功？（铅球重力不可忽略）
[答 案]
1．D 2．D 3．C 4．C 5．A 6．B 7．B
8．解： W = FS
|
| F |
|
| f |
|
| N |
|
| G |
S1 = a1t12
= 
= 4m
S2 = V0t a2t22
V0 = a1t1 = 4m/s
a2 = 
2m/s2
t2 = 
S2 = 8- 
W = F1S1 F2S2 = 
S = S1 S2 = 8m P = FV =3 
4W= 12W
9．解：根据图已知
a = 0.2m/s2
在0~5s 中 F1 = 0.8N
S1 = at2 = 2.5m W1 = FS1 = 2J
在5~10s 中 F2 = f
S2 = Vt = 5m W2 = F2S2 = 2J
在10~15 中 F3 = 0
S3 = 2.5m W3 = F3S3 = 0
F-f = ma
f = F-ma = 0.8-2 0.2 = 0.4N
合力作功：分别为1J、 0 、 -1J。
10．解： V = gt = 10m/s
(mg-f) t1 = 0-mv
f = 600N
在沙坑中的位移为S
S = V0t- 
at2
= 10 0.1- 190 0.01 = 0.05m
Wf = mgs mgH = 165J
| |
