|
第六章 万有引力定律
第五节 《人造卫星、宇宙速度》习题
[练习]
1、某人在一星球上以速度v0竖直上抛一物体,经时间t后物体落回手中。已知星球半径为R ,那么使物体不再落回星球表面,物体抛出时的速度至少为( )

2、两颗人造卫星A、B绕地球做圆周运动,周期之比为TA : TB = 1: 8,则轨道半径之比和运动速率之比分别为( )
A. RA : RB = 4:1; VA : VB = 1:2 B. RA : RB = 4:1; VA : VB = 2:1
C. RA : RB = 1:4; VA : VB = 1:2 D. RA : RB = 1:4; VA : VB = 2:1
3、假如一作圆周运动的人造地球卫星的轨道半径增大到原来的2倍仍作圆周运动,则( )
A.根据公式v=ωr,可知卫星运动的线速度增大到原来2倍
B.根据公式  ,可知卫星所需的向心力将减小到原来的 ,可知卫星所需的向心力将减小到原来的  倍 倍
C.根据公式 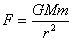 ,可知地球提供的向心力将减小到原来的 ,可知地球提供的向心力将减小到原来的  倍 倍
D.根据上述B和C中给出的公式,可知卫星运动的线速度减小到原来的 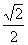 倍 倍
4、某一颗人造地球同步卫星距地面的高度为h,设地球半径为R,自转周期为T,地面处的重力加速度为g,则该同步卫星的线速度的大小为 ( )
A. ((h R)g)0.5 B.2π(h R)/T
C.(R2g/(h R))0.5 D.(Rg)0.5;
5、某球状行星具有均匀的质量密度ρ,当行星自转周期为下列哪个值时,其赤道上的物体将要飞离球面( )。
A.(3π/ρG)0.5 B.(π/ρG)0.5 C. 3πG/4 D. 4πG/3
6、两个球形行星A和B各有一卫星a和b,卫星的圆轨道接近各行星的表面。假如两行星质量之比为MA/MB=p,两行星半径之比RA/RB=q,则两卫星周期之比Ta/Tb为 ( )
A、 B、 C、 D、
7、一航天飞机绕地球作匀速圆周运动,航在飞机内一机械手将物体相对航天飞机无初速地释放于机外,则此物体将: ( )
A.自由落体运动; B.做平抛运动;
C.绕地球做匀速运动; D.与航天飞机相对距离保持不变。
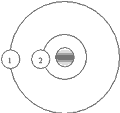
8、如图所示,A、B两颗行星绕同一颗恒星作匀速圆周运动,运转方向相同,A的周期为T1,B的周期为T2,在某一时刻,两行星相遇(即两行星相距最近),则:( )
A、经过一段时间t= T1 T2两行星再次相遇
 B、经过一段时间 B、经过一段时间 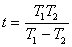 两行星再次相遇 两行星再次相遇
C、经过一段时间 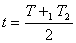 两行星再次相遇 两行星再次相遇
D、经过一段时间  两行星相距最远 两行星相距最远
9、地球半径为R,地面重力加速度为g,地球自转周期为T,地球同步卫星高度为h,则此卫星线速度大小为:( )
A、 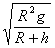 B、 B、 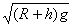 C、 C、 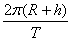 D、 D、 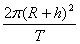
10、甲、乙两颗星球相距很远并远离其它天体。它们的平均密度相等。而半径之比R甲:R乙=4:1,可知在它们表面处的重力加速度之比g甲:g乙= 。
11、两颗卫星在同一轨道平面内绕地球做绕向相同的匀速圆周运动,设地球平均半径为R,a卫星离地高度为0.5R,b卫星离地高度为5R,若某时刻两卫星正好同时通过地面同一点的正上方开始,两卫星第一次出现最远距离的时间是a卫星周期的几倍?
12.经观测,一卫星环绕某行星做圆形轨道运动的半径为r,周期为T,若卫星质量为m.求:(1)行星的质量;(2)卫星向心加速度的大小;(3)作用于卫星上的引力大小.
13、一颗人造卫星的质量为m,离地面的高度为h,卫星做匀速圆周运动,已知地球半径为R,重力加速度为g,求:(1)卫星受到的向心力的大小;(2)卫星的速率;
(3)卫星环绕地球运行的周期
12. 2000年1月26日我国发射了一颗同步卫星,其定点位置与东经98°的经线在同一平面内。若把甘肃省嘉峪关处的经度和纬度近似取为东经98°和北纬α=40°,已知地球半径R、地球自转周期T、地球表面重力加速度g(视为常量)和光速c。试求该同步卫星发出的微波信号传到嘉峪关处的接收站所需的时间(要求用题给的已知量的符号表示)。(2000年广东省高考试题)
 2.在天体运动中,把两颗相距较近的恒星称为双星,已知A、B两恒星质量分别为M1和M2,两恒星相距为L,两恒星分别绕共同的圆心做圆周运动,如图,求两恒星的轨道半径和角速度大小。 2.在天体运动中,把两颗相距较近的恒星称为双星,已知A、B两恒星质量分别为M1和M2,两恒星相距为L,两恒星分别绕共同的圆心做圆周运动,如图,求两恒星的轨道半径和角速度大小。
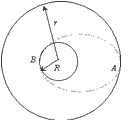 飞船沿半径为r的圆周绕地球运动,其周期为T,假如飞船要返回地面,可在轨道某一点A将速率降低适当数值,从而使飞船沿经地心焦点的椭圆轨道运行,椭圆与地球表面在B点相切,如图所示,已知地球半径为R。试求:飞船由A点到B点所需的时间。 飞船沿半径为r的圆周绕地球运动,其周期为T,假如飞船要返回地面,可在轨道某一点A将速率降低适当数值,从而使飞船沿经地心焦点的椭圆轨道运行,椭圆与地球表面在B点相切,如图所示,已知地球半径为R。试求:飞船由A点到B点所需的时间。
|