| 《直线运动》习题精选 | ||||||||||||||||||||||||||||||||||
|
1.下列所描述的运动中,可能正确的有: A.速度变化很大,加速度很小 B. A. 速度变化方向为正,加速度方向为负 B. C. 速度变化越来越快,加速度越来越小 D. 速度越来越大,加速度越来越小 解:选A、D A . 速度变化很大,若变化时间也很长,加速度可能小;加速度是速度的变化率。 A. 加速度与速度的方向始终相同,都为正或都为负。 C. 速度变化快,加速度一定大。 D. 当加速度与速度方向相同时,无论加速度大小怎么变化,速度都增大。 1. 2.一辆汽车沿平直公路从甲站开往乙站,起动加速度为2m/s2,加速行驶5秒,后匀速行驶2分钟,然后刹车,滑行50m,正好到达乙站,求汽车从甲站到乙站的平均速度?
匀速行驶的速度为: V= a1t1 ……(2) 甲 t1 t2 t3 乙 匀速行驶的位移为: S2 =Vt2 ……(3) 刹车段的时间为: S3 = 汽车从甲站到乙站的平均速度为:
3.已知一物体做匀变速直线运动,加速度为a,试证明在任意一段时间 t 内的平均速度等于该段时间中点 解:物体在匀变速直线运动中,设任意一段时间 t 的初速度为V0,位移为S。 t 时间内的位移为: S=V0t+
时间中点 Vt/2=V0+a
即:在匀变速直线运动中,任意一段时间 t 内的平均速度等于该段时间中点 4.证明:物体做匀变速直线运动,在任意两个连续相等的时间内的位移之差等于一个常数。 证明:设物体在匀变速直线运动中,加速度为a,经过任意一点A的速度为V0,从A点开始,经两个连续相等的时间T的位移分别是S1和S2, V0 V1
根据运动学公式: S1=V0T+ S2=V1T+ V1=V0 + aT ……(3) 两个连续相等的时间内的位移之差: △S = S2-S1 =(V1-V0)T= aT2 因为T是个恒量,小车的加速度也是个恒量,因此△S也是个恒量。即:只要物体做匀变速直线运动,它在任意两个连续相等的时间内的位移之差等于一个常数。 5.汽车以加速度为2m/s2的加速度由静止开始作匀加速直线运动,求汽车第5秒内的平均速度? 解:此题有三解法: (1)用平均速度的定义求: 第5秒内的位移为: S = 第5秒内的平均速度为: V= (2)用推论V=(V0+Vt)/2求:V= (3)用推论V=Vt/2求。第5秒内的平均速度等于4.5秒时的瞬时速度: V=V4。5= a´4.5=9m/S 6.一物体由斜面顶端由静止开始匀加速下滑,最初的3秒内的位移为S1,最后3秒内的位移为 S2,若S2—S1=6米,S1:S2=3:7,求斜面的长度为多少? 解:设斜面长为S,加速度为a,沿斜面下滑的总时间为t 。则:
前3秒内的位移:S1 =
S2—S1=6 …… (4) S1:S2 = 3:7 …… (5) 解(1)—(5)得:a=1m/s2 t= 5s S=12 . 5m 7.物块以V0=4米/秒的速度滑上光滑的斜面,途经A、B两点,已知在A点时的速度是B点时的速度的2倍,由B点再经0.5秒物块滑到斜面顶点C速度变为零,A、B相距0.75米,求斜面的长度及物体由D运动到B的时间? 解:物块作匀减速直线运动。设A点速度为VA、B点速度VB,加速度为a,斜面长为S。 A到B: VB2 - VA2 =2asAB ……(1) C
B到C: 0=VB + at0 ……..(3) 解(1)(2)(3)得:VB=1m/s D a= -2m/s2 D到C: 0 - V02=2aS ……(4) S = 4m 从D运动到B的时间: D到B: VB = V0+ at1 t1=1.5秒 D到C再回到B:t2 = t1+2t0=1.5+2´0.5=2.5(秒) 8.A、B两物体在同一直线下运动,当它们相距 S0=7米时,A在水平拉力和摩擦力的作用下,正以VA= 4米/秒的速度向右做匀速运动,而物体B此时速度VB=10米/秒向右,它在摩擦力作用下以a= -2米/秒2匀减速运动,则经过多长时间A追上B? 若VA=8m/s ,则又经多长时间A追上B? (匀速追匀减速) 解:先判断A追上B时,是在B停止运动前还是后? A B
在5秒内B运动的位移:SB = VBt0 + 因为:SA<SB+S0 ,即:B停止运动时,A还没有追上B。 A追上B的时间为:t = t0 + 若VA=8m/s,则A在5秒内运动的位移为:SA= VAt0=8´5米=40米 因为:SA>SB+S0 ,即:B停止运动前,A已经追上B。 则:VAt/ =VBt/ + t/ 2 - 2t/ - 7 = 0 t/ = 1+2 9.客车以20m/s的速度行驶,突然发现同轨前方120m处有一列车正以6m/s的速度匀速前进。于是客车紧急刹车,以0.8m/s2的加速度匀减速运动,试判断两车是否相撞?(匀减速追匀速) 解:设客车刹车后经t秒两车速度相等,即: V客/=V客 +at ……(1) V客/=V货 ……(2) t = 此时两车距离: DS=S货+S0 - S客 = 6´17.5 + 120 -(20´17.5- 所以两车会相撞。 10. 辆摩托车行驶的最大速度为30m/s。现让该摩托车从静止出发,要在4分钟内追上它前方相 距1千米、正以25m/s的速度在平直公路上行驶的汽车,则该摩托车行驶时,至少应具有多大的加速度? 解:假设摩托车一直匀加速追赶汽车。则:
a = 摩托车追上汽车时的速度: V = at = 0.24´240 = 58 (m/s) ……(3) 因为摩托车的最大速度为30m/s,所以摩托车不能一直匀加速追赶汽车。 应先匀加速到最大速度再匀速追赶。 Vm ≥at1 ……(5) 由(4)(5)得:t1=40/3(秒) a= 11. 一质点沿AD直线作匀加速直线运动,如图,测得它在AB、BC、CD三段的时间均为t,测 得位移AC=L1,BD=L2,试求质点的加速度? 解:设AB=S1、BC=S2、CD=S3 则: A B C D
两式相加:S3-S1=2at2 由图可知:L2-L1=(S3+S2)-(S2+S1)=S3-S1 则:a = 12. 一质点由A点出发沿直线AB运动,行程的第一部分是加速度为a1的匀加速运动,接着做加 速度为a2的匀减速直线运动,抵达B点时恰好静止,如果AB的总长度为S,试求质点走完AB全程所用的时间t? 解:设质点的最大速度为V,前、后两段运动过程及全过程的平均速度相等,均为 全过程: S= 匀加速过程:V = a1t1 ……(2) 匀减速过程:V = a2t2 ……(3) 由(2)(3)得:t1= S = 将V代入(1)得: t = 13. 一个做匀加速直线运动的物体,连续通过两段长为S的位移所用的时间分别为t1、t2,求物体 的加速度? 解:方法(1):设前段位移的初速度为V0,加速度为a,则: 前一段S: S=V0t1 + 全过程2S: 2S=V0(t1+t2)+ 消去V0得:a = 方法(2):设前一段时间t1的中间时刻的瞬时速度为V1,后一段时间t2的中间时刻的瞬时速度为V2。所以: V1= V2=V1+a( 方法(3):设前一段位移的初速度为V0,末速度为V,加速度为a。 前一段S: S=V0t1 + 后一段S: S=Vt2 + V = V0 + at ……(3) 解(1)(2)(3)得相同结果。
《直线运动》练习题 1、甲、乙两辆汽车速度相等,在同时制动后,均做匀减速运动,甲经3s停止,共前进了36m,乙经1.5s停止,乙车前进的距离为:( ) (A)9m (B)18m (C)36m (D)27m 2、质量都是m的物体在水平面上运动,则在下图所示的运动图像中表明物体做匀速直线运动的图像的是( )
3、物体运动时,若其加速度恒定,则物体: (A)一定作匀速直线运动; (B)一定做直线运动; (C)可能做曲线运动; (D)可能做圆周运动。 4、皮球从3m高处落下, 被地板弹回, 在距地面1m高处被接住, 则皮球通过的路程和位移的大小分别是:( ) (A) 4m、4m (B) 3m、1m (C) 3m、2m (D) 4m、2m 5、一石块从楼房阳台边缘向下做自由落体运动, 到达地面, 把它在空中运动的时间分为相等的三段, 如果它在第一段时间内的位移是1.2m, 那么它在第三段时间内的位移是( ) (A) 1.2m (B) 3.6m (C) 6.0m (D) 10.8m 5、物体的位移随时间变化的函数关系是S=4t+2t2(m), 则它运动的初速度和加速度分别是( ) (A) 0、4m/s2 (B) 4m/s、2m/s2 (C) 4m/s、1m/s2 (D) 4m/s、4m/s2
(A) 它们的运动方向相同 (B) 它们的运动方向相反 (C) 甲的速度比乙的速度大 (D) 乙的速度比甲的速度大 7、如图所示, 小球沿斜面向上运动, 依次经a、b、c、d到达最高点e. 已知ab=bd=6m, bc=1m, 小球从a到c和从c到d 所用的时间都是2s, 设小球经b、c时的速度分别为vb、vc, 则( ) (A)
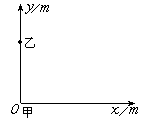
(A) 这两秒内平均速度是2.25m/s (B) 第三秒末即时速度是2.25m/s (C) 质点的加速度是0.125m/s2 (D) 质点的加速度是0.5m/s2 9、物体由静止开始以恒定的加速度a向东运动t s后, 加速度变为向西, 大小不变, 再经过t s时, 物体的运动情况是: ( ) (A) 物体位于出发点以东, 速度为零 (B) 物体位于出发点以东, 继续向东运动 (C) 物体回到出发点, 速度为零 (D) 物体回到出发点, 运动方向向西 10、做匀加速直线运动的列车,车头经过某路标时的速度为v1, 车尾经过该路标时的速度是v2, 则列车在中点经过该路标时的速度是:( ) (A) 11、一辆汽车由静止开始做匀速直线运动,从开始运动到驶过第一个100m距离时,速度增加了10m/s,汽车驶过第二个100m时,速度的增加量是:( ) (A)4.1m/s(B)8.2m/s(C)10m/s(D)20m/s 12、由静止开始做匀加速直线运动的物体, 当经过S位移的速度是v时, 那么经过位移为2S时的速度是: ( ) (A) 2v (B) 4v (C) 13、一个物体从某一高度做自由落体运动, 已知它第一秒内的位移恰为它最后一秒内位移的一半, g取10m/s2, 则它开始下落时距地面的高度为: ( ) (A) 5m (B) 11.25m (C) 20m (D) 31.25m 14、对于做匀变速直线运动的物体:( ) (A) 加速度减小, 其速度必然随之减少 (B) 加速度增大, 其速度未必随之增大 (C) 位移与时间平方成正比 (D) 在某段时间内位移可能为零 15、物体自楼顶处自由落下(不计空气阻力), 落到地面的速度为v. 在此过程中, 物体从楼顶落到楼高一半处所经历的时间为: ( ) (A) v/2 (B) v/(2g) (C) 24、物体做匀速直线运动, 第n秒内的位移为Sn, 第n+1秒内的位移是Sn+1, 则物体在第n秒末的速度是(n为自然数) ( ) (A) (C) 25、下列说法中正确的有: (A)做曲线运动的物体如果速度大小不变,其加速度为零; (B)如不计空气阻力,任何抛体运动都属匀变速运动; (C)做圆周运动的物体,如果角速度很大,其线速度也一定大; (D)做圆周运动物体所受合力必然时刻与其运动方向垂直。 ( ) 26、图是A、B两个质点做直线运动的位移-时间图线.则( ). (A)在运动过程中,A质点总比B质点快 (B)当t=t1时,两质点的位移相同 (C)当t=t1时,两质点的速度相等 (D)当t=t1时,A、B两质点的加速度都大于零 27、一个物体做变加速直线运动,依次经过A、B、C 3点, B为AC的中点,物体在AB段的加速度恒为a1,在BC段的加速度恒为a2,已知A、B、C 3点的速度vA、vB、vC,有vA< vC,且vB=( vA+vC)∕2.则加速度a1 和a2的大小为( ). (A) a1 <a2 (B) a1 =a2 (C) a1 >a2 (D)条件不足无法确定 28、甲、乙、丙三辆汽车同时以相同的速度经过某一路标,此后甲一直做匀速直线运动;乙先加速后减速;丙先减速后加速,它们经过下一个路标时的速度仍相同,则( ) (A)甲车先经过下一个路标 (B)乙车先经过下一个路标 (C)丙车先经过下一个路标 (D)无法判断谁先经过下一个路标 29、一物体沿长为l的光滑斜面,从静止开始由斜面的顶端下滑到斜面底端的过程中,当物体的速度达到末速度的一半时,它沿斜面下滑的长度为( ) (A)l∕4 (B)l( (C)l∕2 (D)l∕ 30、一个物体做匀变速直线运动,若运动的时间之比为t1:t2:t3:…=1:2:3:…,下面有三种说法: ① 相应的运动距离之比一定是s1:s2:s3:…=1:4:9: … ② 相邻的相同时间内的位移之比一定是s1:s2:s3:…=1:3:5: … ③ 相邻的相同时间内位移之差值一定是△s=aT2,其中T为相同的时间间隔. 以上说法正确与否,有( ). (A)只有③ 正确 (B)只有② ③ 正确 (C)都是不正确的 (D)都是正确的 31、小球从3m高处落下,被地板弹回,在1m高处被接住.那么,小球通过的路程和位移的大小分别是( ) (A) 4m,3m (B) 3m,1m (C) 3m,2m (D) 4m,2m 32、以v=36千米/小时的速度沿平直公路行驶的汽车,遇障碍刹车后获得大小为a=4米/秒2的加速度。刹车后3秒钟内,汽车走过的路程为: (A)12米; (B)12.5米; (C)90米; (D)126米。 ( ) 33、如图所示的两条斜线分别代表a、b两物体做直线运动时的速度图线,下列说法中正确的有: (A)在前10秒内,b的位移比a的位移大; (B)b的加速度比a的加速度大; (C)a出发后10秒追上b; (D)10秒时两物体的即时速率相等。 ( ) 二、 填空题: 34、如图所示,质点甲以8m/s的速度从O点沿Ox轴正方向运动,质点乙从点(0,60)处开始做匀速运动,要使甲、乙在开始运动后10s在x轴相遇。 乙的速度大小为________m/s,方向与x轴正方向间的夹角为________。
35、一颗子弹沿水平方向射来,恰穿透三块相同的木板,设子弹穿过木板时的加速度恒定,则子弹穿过三块木板所用的时间之比为________。 36、一个皮球从离地面1.2m高处开始沿竖直方向下落,接触地面后又弹起,上升的最大高度为0.9m,在这过程中,皮球的位移大小是________,位移方向是________,这个运动过程中通过的路程是____________. 37、火车从甲站出发做加速度为 a 的匀加速运动,过乙站后改为沿原方向以 38、以 v = 10 m / s 的速度匀速行驶的汽车,第 2 s 末关闭发动机,第 3s 内的平均速度大小是 9 m / s ,则汽车的加速度大小是____ m / s2 。汽车10 s 内的位移是____ m 。 39、一辆汽车在平直公路上行驶,在前三分之一的路程中的速度是υ1,在以后的三分之二路程中的速度υ2=54千米/小时,如果在全程中的平均速度是U=45千米/小时,则汽车在通过前三分之一路程中的速度υ1= 千米/小时. 40、一物体从16 m 高的A处自由落下,它经过B点时的速率是落地时速率的3 / 4 , 则B点离地的高度为____ m 。( g 取10 m / s2 ) 41、如下图所示,一小球由距地面高为H处自由下落,当它下落了距离为h时与斜面相碰,碰后小球以原来的速率水平抛出。当h=____H时,小球落地时的水平位移有最大值。 43、物体自O点由静止开始作匀加速直线运动,A、B、C、D为某运动轨道上的四点,测得AB=2米,BC=3米,CD=4米,且物体通过AB、BC、CD所用的时间相等,则OA之间的距离为_______米。(如图所示) 44、一物体被抛出后,第1秒末时的速度方向与水平成450角,第2秒末的速度方向恰好水平,则该物体的水平分速大小为_____。 45、在水平直轨道上有两辆长为 46、利用图中所示的装置用自由落体作“测定重力加速度”的实验,在纸带上取得连续的清晰的7个点,打点计时器所用电源的频率为50Hz.用米尺测得第2、3、4、5、6、7各点与第1点的距离d如下表:
利用这些数据求出重力加速度g的测量值为____.(取三位有效数字) 47、一物体从某一高度自由下落,经过一高度为2m的窗户用时间0.4s,g取10m/s2.则物体开始下落时的位置距窗户上檐的高度是____m. 48、图为用打点计时器测定匀变速直线运动的加速度的实验时记录下的一条纸带。纸带上选取1、2、3、4、5各点为记数点,将直尺靠在纸带边,零刻线与纸带上某一点0对齐。由0到1、2、3……点的距离分别用d1、d2、d3……表示,测量出d1、d2、d3……的值,填入表中。已知打点计时器所用交流电的频率为50Hz,由测量数据计算出小车的加速度a和纸带上打下点3时小车的速度v3,并说明加速度的方向。
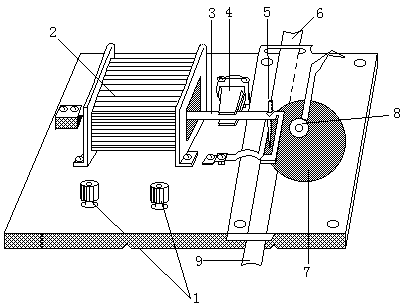
加速度大小a=____m/s2,方向_______,小车在点3时的速度大小v3=______m/s。 49、一物体做匀加速直线运动, 从开始计时起经过时间t通过位移为s, 同时它的速度增大为原来的n倍, 该物体的加速度大小为____________. 50、根据图所示的打点计时器构造图,指出各主要部件的名称:①____,②____,③____,④ ____,⑤____,⑥____,⑦____,⑧____,⑨____
52、电磁打点计时器的电源应是________电源,通常的工作电压为________伏,实验室使用我国民用电时,每隔________秒打一次点,如果每打5个取一个计数点,即相邻两个计数点间的时间间隔为________秒。 53、在“测定匀变速直线运动的加速度”的实验中,用打点计时器记录纸带运动的时间。计时器所用电源的频率为50Hz,图为一次实验得到的一条纸带,纸带上每相邻的两计数点间都有四个点未画出,按时间顺序取0、1、2、3、4、5六个计数点,用米尺量出1、2、3、4、5点到0点的距离如图所示(单位:cm)。 由纸带数据计算可得计数点4所代表时刻的即时速度大小v4=________m/s,小车的加速度大小a=________m/s2。
54、当运动物体所受合外力跟它的速度方向 时,物体就做曲线运动.当运动物体所受恒合外力方向始终跟它的速度方向 时,物体就做匀速圆周运动. 55、在平直的轨道上运动的车厢顶板上A处有油滴落下,油滴落在车厢的地板上,地板上的O点位于A点的正下方,测得油滴落点在O点的后方距O点的距离是车厢顶板和地板的距离的1/10,则可知:(1)车厢正在做______运动,加速度是____;(2)在车厢中的人看油滴的运动应是_____;(3)以地面做参照物,油滴的运动应是_____。 56、如果为磁悬浮列车铺设的平直导轨足够长,列车的牵引力足够大,空气阻力可不计,则列车所能达到的速度的理论极限值为_____________。 57、做匀变速直线运动的物体,从t时刻起,头一秒内的平均速度是1.2m/s。头二秒内的平均速度是1m/s,则(1)物体的加速度是______;(2)t时刻的即时速度是_______。 58、一矿井深125 m,在井口每隔一段时间落下一个小球,当第11个小球刚从井口开始下落时,第1个小球恰好到达井底,则(1)相邻两个小球下落的时间间隔是____ s;(2)这时第3个小球与第5个小球相距_____。(g取10 m/s2) 59、一质点沿ot坐标轴运动,t=0时位于坐标原点,下图为质点做直线运动的速度-时间图线,由图可知,(1)该质点的位移随时间变化的关系式是s=____;(2)在时间t=_____s时质点距坐标原点最远;(3)从t=0到t=20s内质点的位移是_____;通过的路程是______。
61、一条铁链长5m,铁链上端悬挂在某一点,放开后让它自由落下,铁链经地悬点正下方25m处某一点所用的时间是_____s。(取g=10m/s2) 62、如下图所示,棒MN在夹角为300的导轨BA上向左滑行,若在滑行过程中,棒始终垂直于AB边,且速度为1.2m/s,那么MN与AC的交点P沿AC导轨滑行的速度是_____ 。 63、在测定匀变速直线运动的加速度的实验中,使用打点计时器测量小车做匀变速直线运动的加速度,实验得到的一条纸带如下图所示,0、1、2、3……是选用的计数点,每相邻的计数点间还有3个打出的点没有在图上标出。图中还画出了某次实验将米尺靠在纸带上进行测量的情况,读出图中所给的测量点的读数分别是___、____、____和____。计算出物体的加速度的大小是_____m/s(取二位有效数字)。
65、下图给出了汽车从A点出发到B点做直线运动的v-t图线,根据图线填空。
(1)在0 s-40s内汽车做_____运动;加速度是_____。 (2)在40 s-120 s内汽车做______运动;加速度是______ (3)在120 s-200 s内汽车做_____运动;加速度是______;发生的位移是_____。 (4)由图中得到汽车从A点开始到速度大小为10 m/s 时所需的时间是_____。 三、 计算题: 66、物体从A到D由静止开始做匀加速直线运动,B、C把AD分成相等的三段,(1)则物体通过这三段位移的时间之比是_______;(2)平均速度之比是______;(3)物体在B、C、D三点段速度之比是_______。 67、列车沿轨道直线由A地驶向B地, A、B相距为d, 列车从A地由静止出发做匀加速直线运动, 加速度大小为a 68、A、B的运动都在同一直线上, A某时刻的速度为2m/s,以0.2m/s 69、火车正以速率v 70、以10m/s的速度行驶的汽车, 紧急刹车后加速度的大小是6.0m/s2, 求刹车后5.0s内的位移. 71、一辆汽车正在以15m/s的速度行驶,在前方20m的路口处, 突然亮起了红灯, 司机立即刹车, 刹车的过程中汽车的加速度的大小是6m/s2. 求刹车后3s末汽车的速度和汽车距离红绿灯有多远? 72、物体做初速度为2m/s的匀变速直线运动,加速度的方向与初速度相反,大小是0.5m/s. (1) 以初速度的方向为正方向,做出物体运动的位移-时间图线. (2) 说明在t=0时,曲线的斜率代表的意义. (3) 找出曲线的斜率等于0的点,并说明它的意义,它所对应的时间是多少? 73、火车长100m, 从车头离桥头200m处由静止开始以1m/s (1) 整个火车通过全桥的时间. (2) 整个火车通过桥头的时间74、A、B两列火车在同一轨道上同向行驶, A在前, 速度为v (1) A车若仍按原速前进, 两车是否会相撞? 若会相撞, 将在何时何地发生? (2) B车在刹车的同时发出信号, A车司机在收到信号1.5s后加速前进, 求A车的加速度多大时, 才能避免事故发生75、乘客在地铁列车中能忍受的最大加速度是1.4m/s2, 已知两车相距560m, 求: (1) 列车在这两站间的行驶时间至少是多少? (2) 列车在这两站间的最大行驶速度是多大? 76、一平板车,质量M=100千克,停止在水平路面上,车身的平板离地面的高h=1.25米,一质量m=50千克的小物块置于车的平板上,它到车尾端的距离b=1.00米,与车板间的滑动摩擦系数m=0.20,如图所示,今对平板车施一水平方向的恒力,使车向右行驶,结果物块从车板上滑落,物块刚离开车板的时刻,车向右行驶的距离s0=2.0米,求物块落地时,落地点到车尾的水平距离s,(不计路面与平板车间以及轮轴之间的摩擦,取g=10米/秒2) (1)物体的加速度. (2)物体在5s内的位移. 79、火车正以速率v1向前行驶,司机突然发现正前方同一轨道上距离为s处有另一火车,正以较小的速率v2沿同方向做匀速运动,于是司机立刻使火车做匀减速运动,要使两列火车不相撞,加速度a的大小至少应是多少? 80、汽车从静止开始做匀加速直线运动,途中先后经过相隔125m的A、B两点,用10s时间,已知过B点的速度为15m/s,求汽车从出发位置到A点的位移和所用的时间各是多大? 81、做匀加速直线运动的物体,通过某一段长为s的路程所用的时间为t1,接着又继续通过同样长的路程所用的时间为t2,则此物体的加速度为多大? 82、质点以加速度a从静止出发做直线运动。在时刻t,加速度变为2a;时刻2t,加速度变为3a……求在时刻nt时质点的速度以及nt秒内质点通过的总位移。83、甲、乙两物体在不同起点同时开始沿一直线同方向运动(如图所示)。初始位置相距 84、某物体做匀速直线运动的速度为5m/s.分别画出此物体运动的速度图像和位移图像.85、甲车以10m/s的速度在平直的公路上匀速行驶, 在某一时刻经过乙车身边, 此时乙车的速度为2m/s, 加速度 为0.2m/s (1) 当乙车的速度多大时? 乙车落后于甲车的距离最远? 这个最远距离是多大? (2) 当乙车的速度多大时, 乙车追上甲车, 乙车追上甲车用多少时间? 86、一个物体从A点由静止开始作匀加速直线运动到B点,然后作匀减速直线运动到C点静止,AB=s1,BC=s2,由A到C的总时间为t,问:物体在AB,BC段的加速度大小各多少? 87、火车站台上有一位观察者, 站立在火车的第一节车厢前, 火车起动后做匀加速直线运动, 观察者测量出第4节车厢通过他眼前所用的时间是4s, 若车厢的长度是20m, 求火车起动时的加速度. 88、图是用纸带拖动小车用打点计时器测定匀变速运动的加速度打出的一条纸带.A、B、C、D、E为我们在纸带上所选的记数点.相邻计数点间的时间间隔为0.1秒.
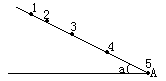
试求: (1)打点计时器打下B、C、D各点时小车的即时速度, (2)小车的加速度. 89、一辆车从静止出发,以加速度a1做匀加速直线运动,加速一段时间后,关闭发动机以加速度a2做匀减速直线运动,直至停下来,总位移是s.求 (1)加速运动时间t1与减速运动时间t2之比; (2)加速运动时间t1; (3)加速运动中通过的位移s1. 90、汽车从静止开始以1.5米/秒2加速度前进,同时在车后20米处一人骑车以6米/秒的速度做匀速运动追赶汽车,骑车者能追上汽车吗?若追不上,则两车间的最小距离是多少? 91、质点以加速度 a从静止出发做匀加速直线运动, 在时刻t, 加速度变为a, 时刻2t, 加速度变为2a, …, 求在时刻nt, 质点的速度以及nt s内它通过的总位移. 92、在火车站站台上有一观察者,在列车开动时给好站在第一节车厢的最前端,列车起动后做匀加速直线运动.5秒末时第一节车厢末端通过观察者(每节车厢等长)求: (1)从开始观察经过多长时间第9节车厢的末端通过观察者; (2)第9节车厢通过观察者的时间. 93、一个物体的初速度是2米/秒,以0.5米/秒2的加速度做匀加速直线运动,求: (1)物体在第3秒末的速度; (2)物体在第4秒初的速度; (3)物体在第4秒内的位移; (4)物体在第4秒内的平均速度; (5)物体在头4秒内的位移; (6)物体在头4秒内的平均速度. 94、有1,2,3,4和5完全相同的小滑块,从斜面底端A点以相同初速度υ0先后依次相隔0.5秒沿斜面向上做匀减速直线运动.第1个滑块沿斜面上滑80厘米时,速度恰好减小为零,此时为第5个滑块开始从A点滑出,如图所示.求: (1)滑块沿斜面上滑的加速度的大小和方向; (2)每个滑块从A点上滑时的初速度; (3)第5个滑块开始从A点上滑时,第3个滑块沿斜面上滑的位移及速度.
95、地震波既有纵波也有横波,纵波和横波在地表附近被认为是匀速传播的.传播速度为别是9.1千米/秒和3.7千米/秒.在一次地震观测站记录的纵波和横波到达该地的时间差是8秒.则地震的震源距这观测站有多远? 96、物体由静止开始沿直线运动,开始时加速度的数值由零逐渐增加,经10秒钟加速度达到最大值,此后加速度保持方向不变,但数值逐渐减小,又经8秒钟加速度减小为零,再运动10秒种.问:在这28秒时间内,物体运动速度如何变化? 97、一辆汽车在十字路口遇红灯,当绿灯亮时汽车以4米/秒2的加速度开始行驶,恰在此时,一辆摩托车以10米/秒的速度匀速驶来与汽车同向行驶,汽车在后追摩托车,求: (1)汽车从路口开始加速起,在追上摩托车之前两车相距的最大距离是多少; (2)汽车经过多少时间能追上摩托车?此时汽车的速度是多大? 98、A,B两小球在同一条直线上,B球静止,A球向B球方向以1米/秒的初速,0.1米/秒2的加速度做匀减速直线运动,2秒末时与B球相碰,碰后A球以碰前速率的一半返回,仍按原加速度数值做匀减速直线运动,B球获得0.4米/秒的初速,以0.4米/秒2的加速度也在做匀减速直线运动,运动方向与A球原运动方向一致.求:当A球停止运动时,A,B两球间的距离. 99、车以10米/秒速度匀速行驶,在距车站25米时开始制动,使车减速前进,到车站时恰好停下.求: (1)车匀减速行驶时的加速度的大小; (2)车从制动到停下来经历的时间. 答案 一、 选择题: 1、A 2、B 3、CD 4、AC 5、C 6、C 7、A 8、D 9、C 10、D 11、AD 12、ABC 13、ABD 14、A 15、C 16、A 17、ABCDE 18、AD 19、C 20、B 21、ABD 22、BD 23、C 24、B 25、B 26、A 27、A 28、B 29、A 30、A 31、D 32、B 33、AD 二、 填空题: 34、10, 370 35、 36、0.3m 竖直向下 2.1m 37、6,2 38、2 ,45 39、33.75 40、7 41、1/2 42、3.5 12 7.75 43、1.125 44、10米/秒 45、v0£ (提示:选择B车为参照物,利用相对运动求解最简单,但不管用什么方法,一定要找出不相碰的两个条件:速度关系、位移关系。) 46、9.72m/s2 47、0.45 48、测量值:1.75 2.90 3.80 4.50 5.00 0.56 与运动方向相反 12.9 49、2s(n-1)/[(n+1)t2] 50、略 51、 52、低压交流,4~6,0.02秒,0.1 53、0.405 0.756 54、不在同一直线上,垂直 55、(1)向前做加速;0.1g(2)匀变速直线运动(3)匀变速曲线运动 56、7.9×103米/秒 57、(1)-0.4m/s2 (2)1.4 m/s 58、(1)0.5 s(2)35 m 59、(1)-4t+0.2t2(2)10 s(3)0;40 m 60、 61、0.21 62、1.39m/s 63、10.00cm; 12.60cm; 22.60cm ; 30.00 cm ;2.5 m/s2 64、25 65、(1)匀加速直线;0.5 m/s2(2)匀速直线;0(3)匀减速直线;-0.25 m/s2; 800 m(4)20 s或160 s 三、 计算题: 66、(1)1:
67、最短时间t= 68、1.5s; 1.425m. 69、(v 70、先判断刹车经历的时间: t=v0/a=10/6.0=1.7s, 则刹车后5.0s经历的位移s= 71、速度为0, 距红绿灯1.25m. 72、(1) 如答图.
(2) t=0时曲线的斜率等于初速度. (3) t=4s时, 曲线的斜率为0, 该时刻的速度为0. 73、(1) 10s (2) 4.5s. 74、(1) B车开始刹车经31s在距开始刹车处810m两车相撞. (2) A车做匀加速运动, 加速度至少为0.15m/s2时, 才能避免相撞. 75、据题意, 列车先以最大加速度a加速行驶至最大速度后, 又以最大加速度a减速行驶直至停止, 这两个过程所用时间相等.如图所示.则: vmax=at/2, s=vmaxt/2, 解得t=40s, vmax=28m/s. 答: 略.
76、约1.6米 77、细线中的张力 解:对A:f-mg-T=0-----(1) 对B:T+f-2mg=0---- (2) (2)-(1) T-mg+T=0 T= f-mg=ma1 a1= 2mg-f=2ma2 a2= sA= sB= d=sA+sB+1=16(m) 78、解: 由s=v0t+ (1)s7=0.5×7+ (2) s5=0.5×5+ s7-s5=4,解出a=2m/s2 (2)s=v0t+ 79、解:从以速度v1行驶的火车发现另一火车开始刹车时计时:设在t时间内追上,应有s1=s2,追上要不相撞,则应有追上时v1′≤v2,.以v2行驶的火车在这段时间内通过的位移为x,则有: v12-v22=2a(s+x) (1) x=v2t (2) t= 解出:a= 80、设汽车的加速度为a,汽车从开始运动到A点的时间为t,经过的位移sA,到A点的速度为vA,则 vB2-vA2=2asAB vB=vA+atAB 可求出a=0.5m/s2, vA=10m/s 所以:vA=atA vA2=2asA 有:sA=100m,tA=20s 81、a= 82、每一个t秒末质点的速度为v1=at,v2=v1+2at=3at=(1+2)at, v3=v2+3at=6at=(1+2+3)at,,vn=vn-1+nat=(1+2+3+……+n)at 因此时刻nt时质点的速度为vn=n(n+1)at/2。每一个t秒内质点的位移为s1=at2/2,s2=v1t+ 2at2/2,s3= v2t+ 3at2/2,……,sn= vn-1t+ nat2/2.nt秒内质点通过的总位移为s=s1+s2+s3+…+sn=n(n+1)(2n+1)at2/12 83、a=2.5米/秒2 84、 (2) 乙车速为18m/s时, 追上甲车, 用时间80s. 86、 87、0.18m/s2. 88、解:设相邻计数点的时间间隔为T=0.1s,则 (1)vB=sAC/2T=0.26m/s vC=sBD/2T=0.30m/s vD=sCE/2T=0.34m/s (2)a= 89、(1)a2:a1;(2) 90、追不上,8米 91、 92、(1)15秒;(2)0.9秒 93、(1)3.5米/秒;(2)3.5米/秒;(3)3.75米; (4)3.75米/秒;(5)12米;(6)3米/秒 94、(1)0.4米/秒2,沿斜面向下;(2)0.8米/秒;(3)0.6米,0.4米/秒 95、49.9千米 96、前10秒钟,加速,速度在增加,中间秒钟也加速,但是增加的比前面的要缓慢些,最后勤部0秒钟是以18秒末时的速度做匀速直线运动 97、(1)12.5米;(2)5秒,20米 98、1米 99、(1)2米/秒;(2)5秒 |
教育最重要的是使人变得更聪明。教育就是要开启人的心智,使人身体好,更主动、积极,行动能力强,更能干。
中文域名: 古今中外.com
英文域名: www.1-123.com
丰富实用的教育教学资料
 斜面长: S =
斜面长: S = 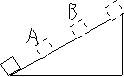 VA = 2VB ……(2)
VA = 2VB ……(2)
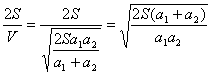
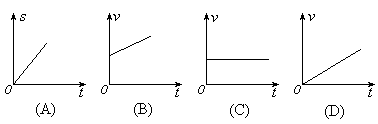
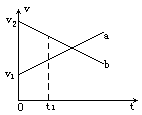 6、甲和乙两个物体在同一直线上运动, 它们的v-t图像分别如图中的a和b所示. 在t1时刻( )
6、甲和乙两个物体在同一直线上运动, 它们的v-t图像分别如图中的a和b所示. 在t1时刻( )
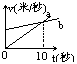
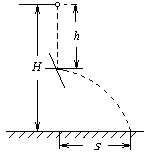 42、小车从坡路上由静止开始下滑,第一秒内的位移是2m,第二秒内的位移是5m,第三秒内的位移是10m,第四秒内的位移是14m,则物体前2s内的平均速度为____m/s,后2s内的平均速度是____m/s,物体在全程的平均速度____m/s.
42、小车从坡路上由静止开始下滑,第一秒内的位移是2m,第二秒内的位移是5m,第三秒内的位移是10m,第四秒内的位移是14m,则物体前2s内的平均速度为____m/s,后2s内的平均速度是____m/s,物体在全程的平均速度____m/s.
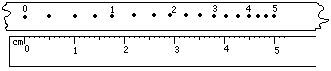
 51、做平抛运动物体的初速,末速的大小分别为n0、n,则它在空中飞行的时间为________。
51、做平抛运动物体的初速,末速的大小分别为n0、n,则它在空中飞行的时间为________。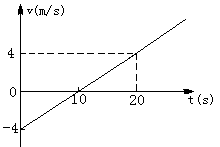 60、一颗子弹沿水平方向射来,恰好穿透3块相同的木板,设子弹穿透木板时的加速度恒定,则子弹穿透3块木板所用的时间之比是_______
60、一颗子弹沿水平方向射来,恰好穿透3块相同的木板,设子弹穿透木板时的加速度恒定,则子弹穿透3块木板所用的时间之比是_______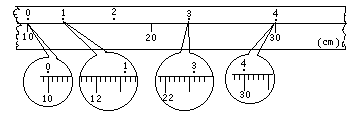 64、竖下悬挂在某点的绳子,放开后让它自由落下,若全绳经地悬点的正上方20m处的A点的时间是1s,则该绳长是_____m(取g=10m/s2)
64、竖下悬挂在某点的绳子,放开后让它自由落下,若全绳经地悬点的正上方20m处的A点的时间是1s,则该绳长是_____m(取g=10m/s2)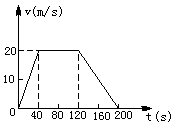
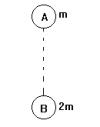 78、一物体做匀加速直线运动,初速度为0.5m/s,第7s内的位移比第5s内的位移多4m.求:
78、一物体做匀加速直线运动,初速度为0.5m/s,第7s内的位移比第5s内的位移多4m.求: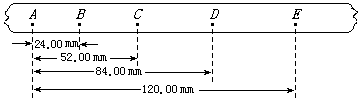
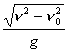
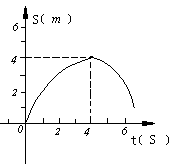
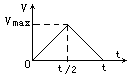
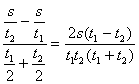
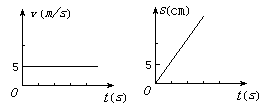 85、(1) 乙车速度为10m/s时, 乙落后于甲车最远, 距离为160m,
85、(1) 乙车速度为10m/s时, 乙落后于甲车最远, 距离为160m, 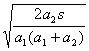 ;(3)
;(3)