|
知识和技能要求
1.掌握密度的概念;
2.会熟练的运用密度及其变形公式进行运算;
3.知道密度单位的写法、读法及换算;
4.通过实验学会测定物质密度的方法,进一步巩固物质密度的概念;
5.学会量筒的使用方法,一是用量筒测量液体体积的方法;二是用量筒测量不规则形状物体体积的方法;
6.尝试用密度知识解决相关的问题,能解释生活中一些与密度有关的物理现象。
重点难点精析
1、密度概念
密度的定义:某种物质单位体积的质量,叫做这种物质的密度。
密度与物体的种类、状态、温度、压强有关。不同的物质,它们的密度值一般是不相同的。
水的密度是:1g/cm3=1×103kg/m3
2、 密度公式
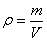
公式中m表示物体的质量,单位用千克;V表示物体的体积,单位用米3;则r表示这物体的材料密度,单位即为千克/米3,如果m的单位克,V的单位用厘米3,则r的单位即为克/厘米3。
密度公式的两个变形公式是: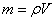 , ,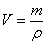 。 。
3、密度单位及换算
国际单位制中,密度的单位是:千克/米3,其他单位:克/厘米3。
换算关系:(以水的密度为例)
1.0×103千克/米3=1.0×103×103克/103厘米3=1.0克/厘米3。
它表示1米3的水质量是103千克,即1厘米3的水质量是1克。
4、密度的测定
根据密度的计算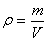 ,可知测定密度的基本方法是: ,可知测定密度的基本方法是:
(1)用天平测出物体的质量m;
(2)如果是形状规则的固体,可用刻度尺测出有关数据,计算出体积V。如正方体的体积V=l3,球体体积V=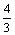 πR3,圆柱体体积V=πr2h等。 πR3,圆柱体体积V=πr2h等。
如果是形状不规则的固体,且不溶于水,则可采用量筒(或量杯),由量筒中水面放入物体后与放入物体前的两次液面示数差来测出固体体积V。
(3)将测出的物体质量m与体积V,代入公式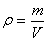 求出组成物体的材料密度。 求出组成物体的材料密度。
5、量筒(量杯)的使用
a.估计被测物体的体积,选择适当的量筒或量杯;
b.观察量筒刻度每一小格表示的数值是多少;
c.量筒必须放置在水平桌面上,然后将液体倒入量筒中;
d.观察量筒液面到达的刻度值,视线要跟液面相平。
量筒和量杯的刻度单位是毫升(或升)。
1升=1分米3, 1毫升=1厘米3
6、密度的常见计算类型
计算质量
若已知物体的体积,和物体的材料密度,则可用公式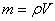 求出物体质量; 求出物体质量;
计算体积
若已知物体的质量和物体的材料密度,则可用公式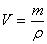 求出物体的体积。 求出物体的体积。
鉴别物质
若已知物体的质量和体积,或已测出质量和体积,即可用公式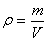 求出密度,通过查密度表,就可知是何种材料构成的物体。 求出密度,通过查密度表,就可知是何种材料构成的物体。
7、密度与社会生活
利用密度确定矿石的种类和价值;
利用密度鉴别酒精,牛奶的浓度;
根据不同密度可以使用风力进行扬场。
农业上利用盐水进行选种;
航天、飞机制造等行业选用密度小的材料。
机器底座要选用密度比较大的材料。
例题解析
 1、一块体积是100厘米3的冰熔化成水后,水的体积( ) 1、一块体积是100厘米3的冰熔化成水后,水的体积( )
A.仍是100厘米3 B.大于100厘米3
C.小于100厘米3 D.无法确定
分析与解:
质量是物体本身的一种属性,当物体的形状、状态、温度、位置改变时,物体的体积、密度等通常会发生变化,但是物体的质量大小是不会变化的。因此,冰熔化成水后,水的质量和冰的质量是相等的,即m冰=m水。
密度是物质的一种特性,它的大小是由物质本身性质决定的,虽然忽略温度的影响,物质的密度大小是不会改变的,但是状态改变时,密度却是要改变的。查密度表可得: ρ水=1.0×103千克/米3, ρ冰=0.9×103千克/米3,即ρ水>ρ冰,而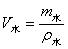 , , 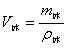 。 。
则可知: V水<V冰。 应选C。
 2、有一块长方形的均匀铝箔,你能不能用天平和刻度尺求出它的厚度?如果能,说出你的办法。 2、有一块长方形的均匀铝箔,你能不能用天平和刻度尺求出它的厚度?如果能,说出你的办法。
分析与解:
利用密度的知识,能够求出该铝箔的厚度。
用天平可测出铝箔的质量,用刻度尺测出铝箔的长和宽后即可求出铝箔的面积,由质量和铝箔的密度能求出铝箔的体积,再由体积、面积即可求出铝箔的厚度。
解: (1)用调节好的天平测出铝箔的质量m。
(2)由公式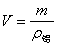 计算出铝箔的体积。 计算出铝箔的体积。
(3)用刻度尺量出铝箔的长a、宽b,计算出铝箔的面积S=ab
(4)由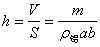 。求出铝箔的厚度。 。求出铝箔的厚度。
 3、一个瓶子最多能装下500g的水,则这个瓶子也能装下下列500g的密度比水___________的物质。 3、一个瓶子最多能装下500g的水,则这个瓶子也能装下下列500g的密度比水___________的物质。
分析与解:
等质量法:
(如果这500g液体的体积小于等于水的体积或者说是瓶子的容积,则能装下)
要使V液<V水,根据密度公式, 需要密度比水大的物质。
等体积法:
看装满瓶子后液体的质量。若装满瓶子液体质量还不够500g则这个瓶子肯定装不下这种液体,如果装满瓶子后质量大于500g,那么500g的液体瓶子肯定也能装下。体积相等,密度大的质量大。密度小的物质质量小,如果密度比水小的质量也比水小那么必然此瓶装不下这种液体。只有密度比水大的才能被装下。
 4、一个用模子浇出的钢铸件,质量是154.4千克,它所用的实心木模的质量是14千克,木模的密度是0.7×103千克/米3,钢的密度是7.8×103千克/米3。试判断这铸件有没有气孔。 4、一个用模子浇出的钢铸件,质量是154.4千克,它所用的实心木模的质量是14千克,木模的密度是0.7×103千克/米3,钢的密度是7.8×103千克/米3。试判断这铸件有没有气孔。
分析与解:
用模子浇出的钢铸件是利用木模来成形的,因此钢铸件和木模有完全相同的形状和体积。但由于是由不同的材料构成的,因此它们的密度和质量都不同。
判断钢铸件有没有气孔,实际上就是判断钢铸件是不是完全实心的。
由木模的质量和密度可求出木模的体积,这等于钢铸件的体积;由钢铸件的体积和密度可求出实心钢铸件的质量(即没有气孔时的质量),和钢铸件的实际质量相比较,即可判断出钢铸件有无气孔。
另外,如通过比较体积和密度也能判断出钢铸件有无气孔。
解: m1=154.4千克,m2=14千克, ρ1=7.8×103千克/米3, ρ2=0.7×103千克/米3
实心木模的体积:
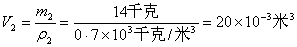
钢铸件的体积:
V1=V2=20×10-3米3
钢铸件如没有气孔,则其质量应该是:
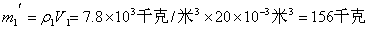
∵156千克>154.4千克
说明此钢铸件有气孔。
 5、一空瓶质量200克,装满水后总质量为700克,现向一空瓶内装一些金属颗粒,使瓶和金属质量共为1000克,然后再向瓶内灌满水,用天平测得此时的总质量为1410克。求瓶内金属的密度。 5、一空瓶质量200克,装满水后总质量为700克,现向一空瓶内装一些金属颗粒,使瓶和金属质量共为1000克,然后再向瓶内灌满水,用天平测得此时的总质量为1410克。求瓶内金属的密度。
分析与解:
由空瓶质量及装满水后的总质量可求出瓶内的水的质量,并再由水的密度可求出水的体积,即瓶的容积。
由空瓶质量及瓶和金属颗粒的总质量可求出金属颗粒的质量;由瓶内再灌满水后的总质量可求出后装入的水的质量,并进一步求出其体积;用瓶内容积减去后装入的水的体积即可求出金属颗粒的体积。
最后,将金属颗粒的质量和体积代入公式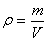 即可求出该金属的密度。 即可求出该金属的密度。
解: m1=200克,m2=700克,m3=1000克,m4=1410克, ρ水=1克/厘米3
瓶内装满水时,所盛水的质量:m水=m2-m1=700克-200克=500克
盛满水时,水的体积: 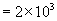
则瓶内容积:V=V水=500厘米3
瓶内金属颗粒的质量:m金=m3-m1=1000克-200克=800克
瓶内后装入的水的质量:
m水=m4-m3=1410克-1000克=410克
瓶内后装入的水的体积:

金属颗粒的总体积:
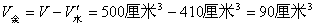
金属颗粒的密度:
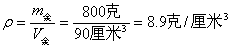
即金属密度为8.9×103千克/米3
 6、2m3的水结成冰,体积增大了多少?(冰的密度:0.9×103kg/m3) 6、2m3的水结成冰,体积增大了多少?(冰的密度:0.9×103kg/m3)
分析与解
本题可采用“分析法”.所谓分析法,就是从题目所要求的物理量出发,联系运用的物理规律和公式,通过逐步推理直到已知条件满足,可以求出为止,要求体积增大了多少,已知水的体积,则需求冰的体积,已知冰的密度,根据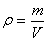 ,则需求出冰的质量,而冰的质量与水的质量相等是题目中隐含的已知条件,即水结成冰,密度改变,体积改变,但质量不变,所以求冰的质量就转化成求水的质量,而水的密度与体积都已知,此题可解。 ,则需求出冰的质量,而冰的质量与水的质量相等是题目中隐含的已知条件,即水结成冰,密度改变,体积改变,但质量不变,所以求冰的质量就转化成求水的质量,而水的密度与体积都已知,此题可解。
解法一 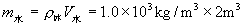
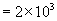 kg kg
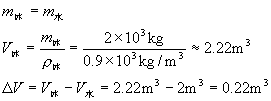
本题还可以用比例法求解,因为冰、水的质量相等,所以冰、水的体积跟它们的密度成反比。
解法二 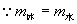
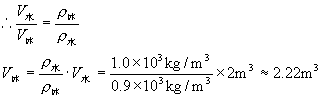
体积增大为2.22m3
 7、石油可以用油罐车来运输,它的密度是0.85×103kg/m3,如果每节油罐车的容量是80m3,运输2000t石油需多少节油罐车? 7、石油可以用油罐车来运输,它的密度是0.85×103kg/m3,如果每节油罐车的容量是80m3,运输2000t石油需多少节油罐车?
分析与解
本题是利用密度知识联系实际的问题,可先计算2000t石油有多大体积,除以每节油罐车的容量,即得所需多少节油罐车。此题也可以先计算出每节油罐车所装石油的质量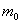 ,然后用2000t石油的总质量除以每节油罐车所装石油质量 ,然后用2000t石油的总质量除以每节油罐车所装石油质量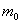 ,即得所需油罐车的节数。 ,即得所需油罐车的节数。
已知: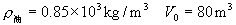

求: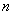
解法一 2000t石油的总体积
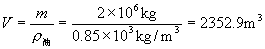
油罐车的节数
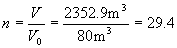
应取整数30节
解法二 每节油罐车所装石油质量
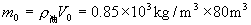
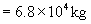
所需油罐车的节数
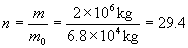
应取整数30节
答:需30节油罐车
|