|
万有引力定律
-------------基础能力
1.发现万有引力定律和测出引力常数的科学家分别是 ( C )
A.开普勒、卡文迪许 B.牛顿、伽利略
C.牛顿、 卡文迪许 D.开普勒、伽利略
2.下列关于地球同步卫星的说法正确的是 ( BD )
A.它的周期与地球自转同步,但高度和速度可以选择,高度增大,速度减小
B.它的周期、高度、速度都是一定的
C.我们国家发射的同步通讯卫星定点在北京上空
D.我国发射的同步通讯卫星也定点在赤道上空
3.某行星的质量是地球质量的6倍,半径是地球半径的1.5倍,则此行星的第一宇宙速度约为 ( A )
A.16km/s B.32km/s C.4km/s D.2km/s
4.两颗质量相等的人造地球卫星a、b绕地球运行的轨道半径ra=2rb,下面说法中正确的是( B )
A. 由公式F=mv2/r可知,卫星a的向心力是b的1/2
B. 由公式F=GMm/r2可知,卫星a的向心力是b的1/4
C. 由公式F=mv2/r可知,卫星a的向心力是b的2倍
D.以上说法都不对
5.若地球表面处的重力加速度为g,而物体在距地球表面3R(R为地球半径)处,由于地球作用而产生的加速度为g’,则g/g’为 ( D )
A.1 B.1/9 C.1/4 D.1/16
6.人造卫星在太空绕地球运行中,若天线偶然折断,天线将 ( A )
A.继续和卫星一起沿轨道运行 B.做平抛运动,落向地球
C.由于惯性,沿轨道切线方向做匀速直线运动,远离地球
D.做自由落体运动,落向地球
7.设行星绕恒星运动轨道是圆,则其运动周期为T的平方与其运行轨道半径R的三次方之比为常数,即T2/R3=K,那么K的大小决定于 ( B )
A.只与行星质量有关 B. 只与恒星质量有关
C. 与行星和恒星质量都有关 D. 与恒星的质量及行星的速率都无关
8.两星球质量比为p,半径比为q,那么在它们表面重力加速度之比为: ( A )
A.p/q2 B.pq2 C.p/q D.Pq
9.卡文迪许巧妙地利用扭秤装置,第一次在实验室里测出了引力常量,在他的实验装置中,为了测量极小的引力而采取的措施是: ( ABC )
A. 将测量力变成测量力矩
B. 使固定小球的质量尽可能大些
C. 用小镜反射光显示扭秤的偏转情况
D.把实验装置放在恒温箱内
10.关于人造卫星及其中物体超重和失重问题,下列说法正确的是: ( AC )
A. 在发射过程中向上加速时产生超重现象
B. 在降落过程中向下减速时产生失重现象
C. 进入轨道时作匀速圆周运动,产生完全失重现象,但仍受重力作用
D. 失重是由于地球对卫星内物体的作用力减小而引起的
11.用m表示地球同步卫星的质量,h表示它离地面的高度,R0表示地球的半径,go表示地球表面重力加速度,ωo表示地球自转角速度,则同步卫星所受地球对它的引力大小可用下列式子表示的是: ( BC )
A.mωo2h B.mωo2(Ro h)
C.m go R02/(Ro h)2 D.m (go R02ωo4)1/3
12.宇宙飞船进入一个围绕太阳运行的近乎圆形的轨道上运行假如轨道半径是地球绕太阳运行轨道半径的4倍,那么宇宙飞船绕太阳运行周期是: ( B )
A.3年 B.8年 C.27年 D.81年
13.物体在月球表面上的重力加速度为地球表面上的1/6,这说明 ( D )
A. 地球半径是月球半径的6倍
B. 月球的质量是地球质量的1/6
C. 月球吸引地球的引力是地球吸引月球引力的1/6
D.物体在月球表面的重力是地球表面重力的1/6
14. 两颗人造地球卫星,都绕地球作圆周运动,它们的质量相等,轨道半径之比r1 /r2=1/2,则它们的速度大小之比V1/V2等于 ( B )
A. 2 B. 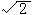 C. 1/2 D. 4 C. 1/2 D. 4
15.两行星A和B各有一颗卫星a和b,卫星的圆轨道接近各自行星表面,假如两行星质量之比MA:MB=2 : 1,两行星半径之比RA:RB=1 : 2,则两个卫星周期之比Ta:Tb为 ( A )
A.1 : 4 B.1 : 2
C.1 : 1 D.4 : 1
16.两颗人造卫星A、B绕地球作圆周运动, 周期之比为TA:TB=1:8,则轨道半径之比和运动速率之比分别为 ( C )
A.RA:RB=4:1 , VA:VB=1:2
B.RA:RB=4:1 , VA:VB=2:1
C.RA:RB=1:4 , VA:VB=2:1
D.RA:RB=1:4 , VA:VB=1:2
17.已知万有引力常量G,某行星的半径和绕该星表面运行的卫星的周期,可以求得下面哪些量? ( ABD )
A.该行星的质量 B.该行星表面的重力加速度
C.该行星的同步卫星离其表面的高度 D.该行星的第一宇宙速度
18.已知月球中心到地球中心的距离大约是地球半径的60倍,则月球绕地球运行的向心加速度与地球表面的重力加速度的之比为 ( C )
(A)1:60 (B)1:  (C)1:3600 (D)60:1 (C)1:3600 (D)60:1
19.某天体半径是地球半径的K倍,密度是地球的P倍,则该天体表面的重力加速度是地球表面重力加速度的 ( C )
(A)  倍 (B) 倍 (B) 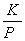 倍 (C) KP倍 (D) 倍 (C) KP倍 (D) 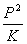 倍 倍
20.设想把一质量为m的物体放在地球的中心,这时它受到地球对它的万有引力是 ( A )
(A)0 (B)mg (g=9.8m/s2) (C)∞ (D)无法确定
21.一物体在某星球表面四周自由落体,在连续两个1秒内下落的高度依次为12m,20m,则该星球表面的重力加速度的值为 ( C )
(A)12m/s2 (B) 10m/s2 (C ) 8m/s2 (D) 16m/s2
22.人造地球卫星A和B,它们的质量之比为mA:mB=1:2,它们的轨道半径之比为2:1,则下面的结论中正确的是 ( BC ).
(A)它们受到地球的引力之比为FA:FB=1:1
(B)它们的运行速度大小之比为vA:vB=1: 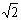
(C)它们的运行周期之比为TA:TB=2 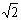 :1 :1
(D)它们的运行角速度之比为 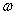 A: A: 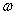 B=3 B=3  :1 :1
23.绕地球做匀速圆周运动的人造卫星,轨道半径越大的卫星,它的 ( D )
A. 线速度越大 B. 向心加速度越大
C. 角速度越大 D. 周期越大
24.1999年11月20日,我国成功发射了“神舟”号宇宙飞船,该飞船在绕地球运行了14圈后在预定地点安全着落,若飞船在轨道上做的是匀速圆周运动,则运行速度v的大小( A )
A.v<7.9km/s B.v=7.9km/s C.7.9km/s<v<11.2km/s D.v=11.2km/s
25.一颗小行星环绕太阳做匀速圆周运动的半径是地球公转半径的4倍,则这颗小行星的运转周期是 ( B )
A.4年 B.8年 C.12年 D.16年
26.甲、乙两卫星分别环绕地球做匀速圆周运动,已知甲、乙的周期比值为T1:T2=8,则两者的速率比值V1:V2为 ( A )
A.1/2 B.1 C. 2 D.4
27.1990年5月,紫金山天文台将他们发现的第2752号小行星命名为吴健雄星,该小行星的半径为16km。若将此小行星和地球均看成质量分布均匀的球体,小行星密度与地球密度相同。已知地球半径R=6400km,地球表面重力加速度为g,这个小行星表面的重力加速度为(D)
A.20g B. 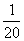 g C.400g D. g C.400g D. 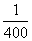 g g
28. 设地球表面的重力加速度为10米/秒2,有一质量为60千克的人到另外一个星球,该星球的质量是地球质量的1/6,该星球的半径是地球半径的1/2,则在这一星球上,这个人的质量和所受到的重力分别是 ( B )
(A)60千克,600牛 (B)60千克,400牛
(C)40千克,400牛 (D)40千克,600牛
29.把太阳系中各行星的运动近似看作匀速圆周运动,则离太阳越远的行星 ( BCD )
(A)周期越小; (B)线速度越小; (C)角速度越小; (D)加速度越小;
30.当地球卫星绕地球作匀速圆周运动时,其实际的绕行速率 ( B )
(A)一定等于7.9千米/秒 (B)一定小于7.9千米/秒
(C)一定大于7.9千米/秒 (D)介于7.9千米/秒和11.2千米/秒之间
31.若已知某行星绕太阳公转的半径为r,公转的周期为T,万有引力常量为G,则由此可求出 ( B )
(A)某行星的质量; (B)太阳的质量;
(C)某行星的密度; (D)太阳的密度。
32.一个半径比地球大2倍,质量是地球的36倍的行星,它表面的重力加速度是地球表面的重力加速度的 ( C )
(A)6倍; (B)18倍; (C)4倍; (D)13.5倍;
33.若人造卫星绕地球作匀速圆周运动,则下列说法正确的是 ( BD )
A.卫星的轨道半径越大,它的运行速度越大
B.卫星的轨道半径越大,它的运行速度越小
C.卫星的质量一定时,轨道半径越大,它需要的向心力越大
D.卫星的质量一定时,轨道半径越大,它需要的向心力越小
34.由于地球上的物体都随地球自转,则下列说法错误的是: ( AD )
A. 地球上物体都具有自转的向心加速度
B. 同一纬度,高处物体自转的向心加速度大
C. 赤道地区物体自转向心加速度比两极大
D.地球对地球上物体的万有引力数值上等于物体随地球自转的向心力
35.关于三个宇宙速度下列说法中正确的是: ( AB )
A. 环绕速度是人造卫星的最小发射速度
B. 环绕速度是人造卫星绕地球做匀速圆周运动的最大速度
C. 人造卫星绕地球做匀速圆周运动的最大速度是11.2km/s
D.由B可推知,物体绕太阳做圆周运动的最大速度是16.7km/s
(D)空间实验站及仪器绕地球作匀速圆周运动的向心力是由地球对它的引力提供
|